Принципы построения и свойства моделей.

Модель – это физическая или абстрактная система, адекватно представляющая объект исследования. Абстрактная модель – описание объекта на некотором формальном языке. Абстрактные модели – ее компоненты не физические модели, а понятия, в качестве которых наиболее часто используются математические отношения. Абстрактная модель, основанная на математическом отношении, называется математической моделью. Математическая модель имеет форму функциональной зависимости:

Y=F(x).

Y – набор характеристик Y={y₁, y₂, …, y_m}

X – набор параметров X={x₁, x₂, …,x_n}

F – функция воспроизводящая модель.

Модель создается исходя из цели исследования, которая определяет

1). состав характеристик Y,

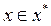2). состав параметров X,

3). область определения модели

4). задается точность, как предельная допустимая погрешность оценки Y на модели. Модель, построенная на основе этих принципов, называется адекватной системе моделью. Свойства адекватности модели являются относительными. Они связаны с целью исследования. Больше всего адекватность определяется в точности воспроизведения. Если не найдена точность, то модель не может считаться адекватной. Высокая точность может быть получена только в узкой окрестности точки x. Чем больше окрестность точки x, тем более сложной должна быть модель.

Кроме адекватности, к свойствам модели относятся:

1). мощность,

2). размерность,

3). сложность вычислений.

Размерность – число величин, представленных в модели, параметры и характеристики(X и Y).

Сложность вычислений – оценивается числом операций, приходящихся на одну реализацию оператора F. Напрямую связана с затратами вычислительного времени.

Т.к. процессы, протекающие в ВС, носят характер случайных, то в качестве математической базы используемой как метод исследования ВС наиболее часто используют аппарат теории вероятностей и математической статистике. При этом случайные величины, соответствующие параметрам, характеристикам и другими элементами моделей могут быть представлены на разных уровнях, среди которых наиболее часто используются следующие:

1). Статистическая выборка,

2). Закон распределения случайной величины,

3). Математическое ожидание и дисперсия,

4). Математическое ожидание.