Максимизация прибыли монополией.

Сформулируем условие максимизации прибыли для монополиста. Для этого найдем производную прибыли (П) по Q и приравняем ее к нулю:

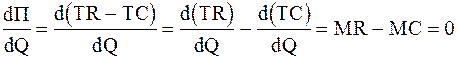или

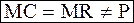(3.2.)

Вернемся к числовому примеру. Если при увеличении объема производства на 1 изделие общие затраты монополиста увеличиваются на 250 ден. ед., то его прибыль увеличивается на (300-250) ден. ед. и монополист заинтересован в расширении производства и в повышении цены. Он будет это делать до тех пор, пока его предельная выручка не сравняется с предельными затратами. Если же, наоборот, МС>MR и равны, например, 350 ден. ед., монополист, стремясь максимизировать прибыль, будет сокращать объем производства и повышать цену.

Чтобы максимизировать прибыль, фирма должна достичь такого объема продукции, при котором предельный доход равен предельным издержкам.

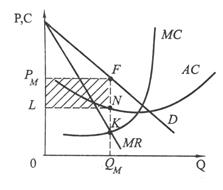
Рис. 3.5. Максимизация прибыли монополией в коротком периоде

Итак, стремясь к максимуму прибыли, монополия выбирает объем производства, при котором МС = МR. Точка пересечения этих графиков обозначена точкой К, так как точку максимизации прибыли монополией называют точкой Курно. На рис 3.4. прибыль монополии в расчете на единицу продукции монопольного объема Q_M равна длине отрезка FN (P_M>AC). Суммарная прибыль монополии на весь выпуск равна площади PFNL.

Монополист,как правило, производит меньше, чем при совершенной конкуренции и по более высоким ценам.