Достаточное условие экстремума.
Пусть функция определена в критической точке x0 и дифференцируема в некоторой окрестности этой точки, за исключением, может быть, самой x0. Если «при переходе» через точку x0 слева направо производная меняет знак с плюса на минус, то x0 – точка максимума; с минуса на плюс – точка минимума.

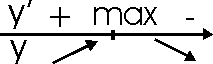
Доказательство:
Пусть производная меняет знак с «+» на «-».
Тогда слева от х0, т.е. на (х0-δ,х0) 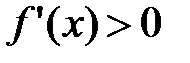 .
.
| y |
| x |
| x0 |
| f(x0) |
| x0+d |
| x0-d |
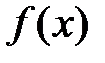 возрастает.
возрастает.
Справа от х0, т.е. на (х0, х0+δ) 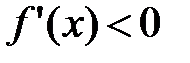 .
.
Þ справа от х0 функция 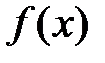 убывает.
убывает.
Т.о. в окрестности точки х0 выполняется
неравенство 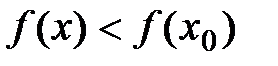 .
.
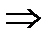 х0 – точка локального максимума.
х0 – точка локального максимума.
Аналогично доказывается для минимума.
Ч.т.д.
Пример: Исследовать функцию на монотонность и найти точки экстремума.
а) 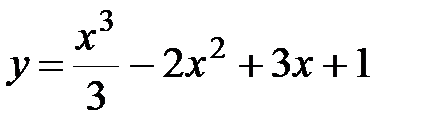 .
.
1. Область определения функции D(y)=R.
2. 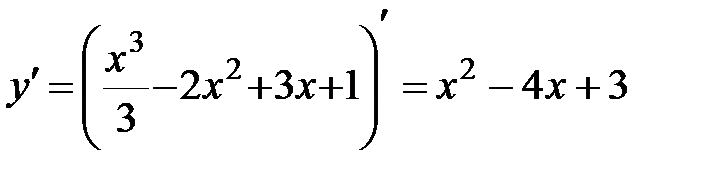 .
.
Критические точки: 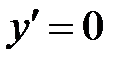 .
. 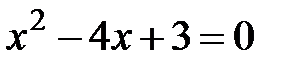 Þ
Þ 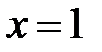 ,
, 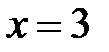 .
.
| x | (-∞;1) | x=1 | (1;3) | x=3 | (3;+∞) |
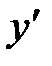
| + | – | + | ||
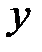
| возрастает | max
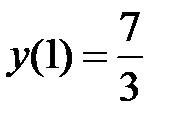
| убывает | min y(3)=1 | возрастает |
б) 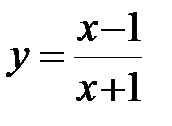 .
.
1. Область определения функции D(y): x¹-1.
2. 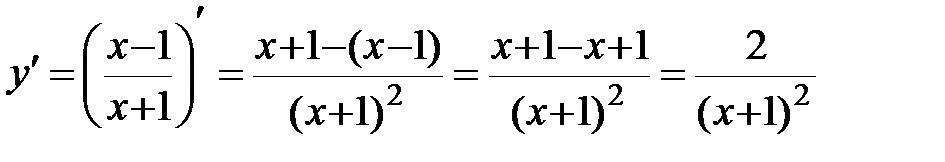 ;
;
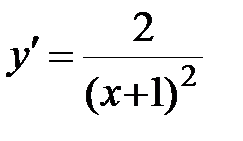 .
.
Критические точки: 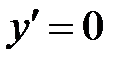 , т.е. числитель равен нулю Þ нет точек;
, т.е. числитель равен нулю Þ нет точек;
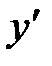 – не существует, т.е. знаменатель равен нулю Þ
– не существует, т.е. знаменатель равен нулю Þ 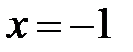 .
.
| x | (-∞;-1) | x=-1 | (-1;+∞) |
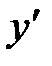
| + | не существует | + |
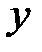
| возрастает | не существует | возрастает |
Точек экстремума нет.
Наибольшее и наименьшее значения функции на отрезке.
Пусть функция 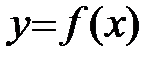 определена и непрерывна на замкнутом промежутке [a;b] и имеет внутри этого промежутка конечную производную.
определена и непрерывна на замкнутом промежутке [a;b] и имеет внутри этого промежутка конечную производную.
Тогда по второй теореме Вейерштрасса она на этом отрезке принимает свои наибольшее и наименьшее значения.
Очевидно, что эти значения могут достигаться либо в критических точках, либо на концах отрезка.
Поэтому для нахождения наибольшего и наименьшего значений функции применяют следующий алгоритм решения:
1. Находим критические точки функции. Отбираем те точки, которые принадлежат данному отрезку.
2. Вычисляем значения функции в найденных точках.
3. Вычисляем значения функции на концах отрезка.
4. Из полученных значений функции выбираем наибольшее и наименьшее.
Исследование функции на максимум и минимум с помощью производной второго порядка.
Пусть функция 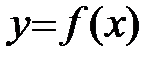 определена и непрерывна на промежутке (a;b).
определена и непрерывна на промежутке (a;b).
Теорема.
Пусть 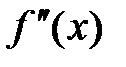 существует и непрерывна в некоторой окрестности точки
существует и непрерывна в некоторой окрестности точки 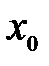 . Пусть
. Пусть 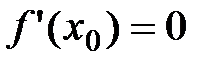 . Если
. Если 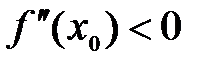 , то в точке
, то в точке 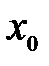 функция имеет максимум; если
функция имеет максимум; если 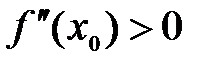 , то в точке
, то в точке 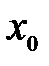 функция имеет минимум.
функция имеет минимум.
Доказательство:
Докажем для максимума.
Пусть 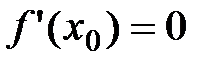 . Пусть
. Пусть 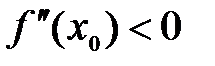 .
.
Так как, по условию, 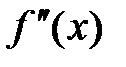 непрерывна в некоторой окрестности точки
непрерывна в некоторой окрестности точки 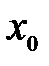 , то найдется некоторая окрестность
, то найдется некоторая окрестность 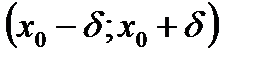 , во всех точках которой вторая производная
, во всех точках которой вторая производная 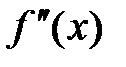 будет отрицательна.
будет отрицательна.
Так как 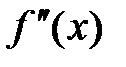 есть производная от первой производной, т.е.
есть производная от первой производной, т.е. 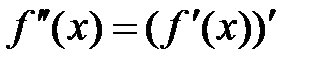 , то из условия
, то из условия 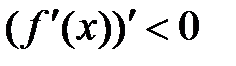 следует, что
следует, что 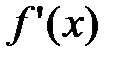 убывает на промежутке, содержащем точку
убывает на промежутке, содержащем точку 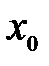 , т.е. в окрестности
, т.е. в окрестности 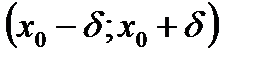 .
.
Так как 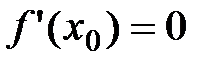 , Тогда слева от
, Тогда слева от 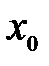 , т.е. на (х0-δ,х0) имеем
, т.е. на (х0-δ,х0) имеем 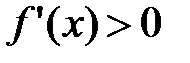 , а справа от
, а справа от 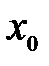 , т.е. на (х0, х0+δ) имеем
, т.е. на (х0, х0+δ) имеем 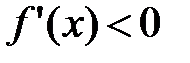 , т.е. производная
, т.е. производная 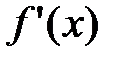 «при переходе» через точку x0 слева направо меняет знак с плюса на минус. А это значит, что точка
«при переходе» через точку x0 слева направо меняет знак с плюса на минус. А это значит, что точка 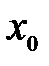 – точка максимума.
– точка максимума.
Аналогично доказывается для минимума.
Ч.т.д.
Если в критической точке 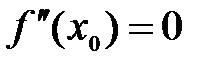 , то в этой точке может быть или максимум, или минимум или не быть ни максимума, ни минимума. В этом случае исследование проводится с помощью первой производной.
, то в этой точке может быть или максимум, или минимум или не быть ни максимума, ни минимума. В этом случае исследование проводится с помощью первой производной.
Пример: Исследовать на максимум и минимум функцию.
а) 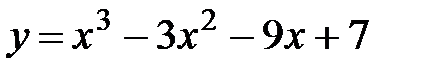 .
.
1. Область определения функции D(y)=R.
2. 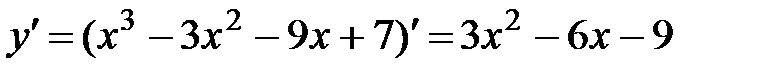 .
.
Критические точки: 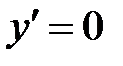 .
. 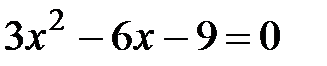 ,
, 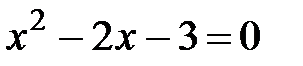 Þ
Þ 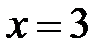 ,
, 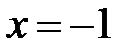 .
.
3. 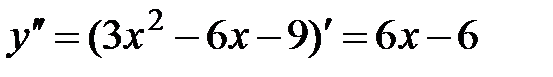 .
.
| x | x=-1 | x=3 |
| -12 | |
| max y(-1)=12 | min y(3)=-20 |
б) 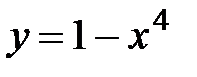 .
.
1. Область определения функции D(y)=R.
2. 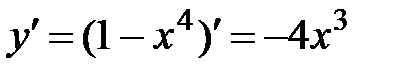 .
.
Критические точки: 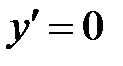 .
. 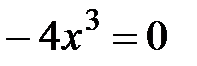 Þ
Þ 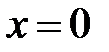 .
.
3. 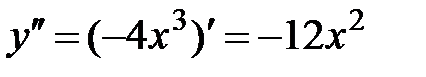 .
.
| x | (-∞;0) | x=0 | (0;+∞) |
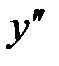
| |||
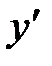
| + | – | |
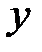
| возрастает | max y(0)=1 | возрастает |
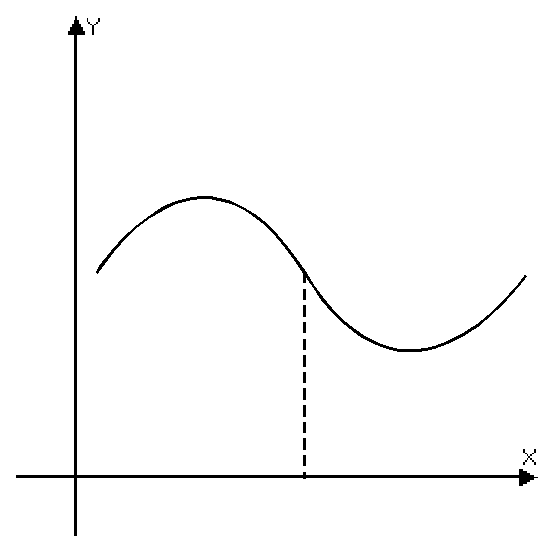
Выпуклые и вогнутые функции.
Пусть функция 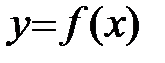 дифференцируема на интервале (a;b). Тогда на этом интервале в каждой точке графика функции существует касательная, причем не параллельная оси OY.
дифференцируема на интервале (a;b). Тогда на этом интервале в каждой точке графика функции существует касательная, причем не параллельная оси OY.
Определение: Функция называется выпуклой, если ее график лежит над любой касательной, проведенной к этому графику.
Определение: Функция называется вогнутой, если ее график лежит под любой касательной, проведенной к этому графику.
На разных участках промежутка функция может быть выпуклой или вогнутой.
Признак выпуклости.
Пусть функция 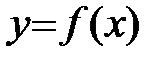 имеет на интервале (a;b) непрерывную производную второго порядка. Если
имеет на интервале (a;b) непрерывную производную второго порядка. Если 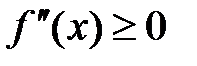 , то функция выпукла на промежутке (a;b). Если
, то функция выпукла на промежутке (a;b). Если 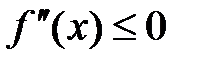 , то функция вогнута на промежутке (a;b).
, то функция вогнута на промежутке (a;b).
Доказательство:
Пусть для определенности на (a;b) 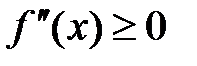 .
.
Возьмем точку x0Î(a;b) и составим уравнение касательной к графику функции в точке с абсциссой x0:
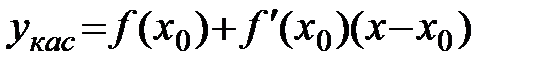 (1)
(1)
Разложим функцию 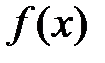 в окрестности точки x0 по формуле Тейлора, причем возьмем два члена разложения и остаточный член:
в окрестности точки x0 по формуле Тейлора, причем возьмем два члена разложения и остаточный член:
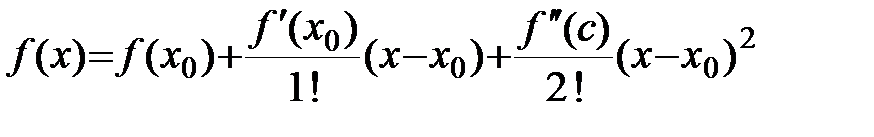 ,
, 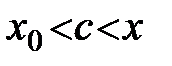 (2)
(2)
| x |
| y |
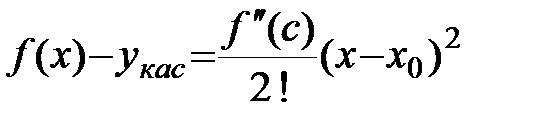 .
.
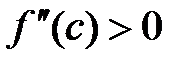 на (a;b)
на (a;b) 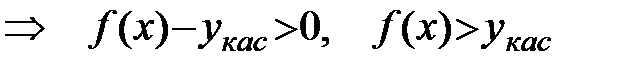 .
.
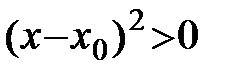
График функции проходит над касательной.
Тогда по определению: функция выпукла.
Вогнутость доказывается аналогично.
Ч.т.д.
Замечание: Условие 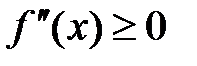 (
( 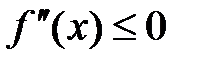 ) является не только достаточным, но и необходимым для выпуклых (вогнутых) функций.
) является не только достаточным, но и необходимым для выпуклых (вогнутых) функций.
Определение: Точка, отделяющая промежуток выпуклости функции от промежутка ее вогнутости, называется точкой перегиба.
Необходимые условия существования точки перегиба функции.
Пусть функция 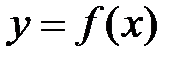 в точке x0 имеет точку перегиба. Если в этой точке существует производная второго порядка, то она обращается в ноль
в точке x0 имеет точку перегиба. Если в этой точке существует производная второго порядка, то она обращается в ноль 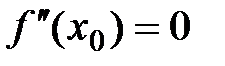 или не существует.
или не существует.
Точки перегиба следует искать среди точек, вторая производная которых равна нулю (y²=0) или не существует. Такие точки называются критическими точками второго рода.
Достаточное условие точки перегиба функции.
Пусть 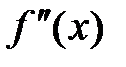 непрерывна в окрестности точки
непрерывна в окрестности точки 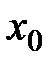 , за исключением, может быть, самой точки
, за исключением, может быть, самой точки 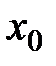 . Если «при переходе» через
. Если «при переходе» через 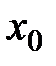
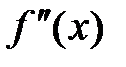 меняет знак, то точка
меняет знак, то точка 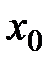 — точка перегиба.
— точка перегиба.
Доказательство:
Пусть «при переходе» через точку 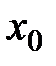
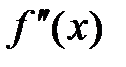 меняет знак с «+» на «-».
меняет знак с «+» на «-».
| + |
| - |
| x0 |
Тогда слева от точки 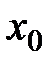 — функция выпукла, а справа — вогнута. Тогда по определению: точка
— функция выпукла, а справа — вогнута. Тогда по определению: точка 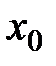 — точка перегиба.
— точка перегиба.
Ч.т.д.
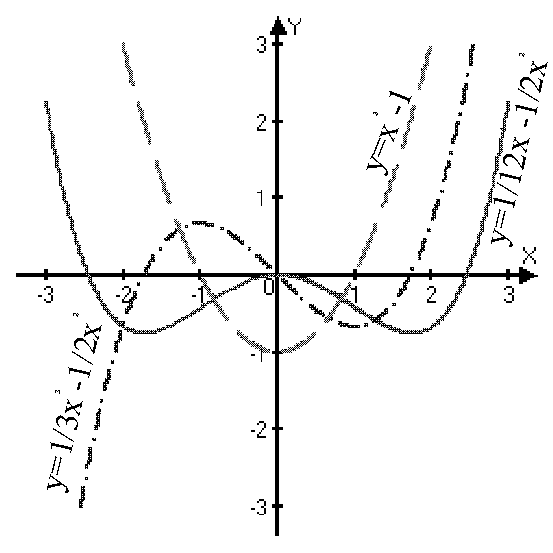 Пример: Исследовать функцию на перегиб.
Пример: Исследовать функцию на перегиб. 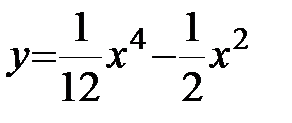 .
.
D(y)=R.
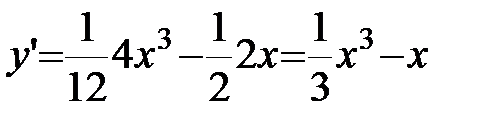 ;
; 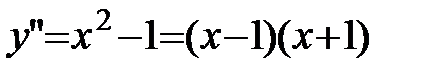 .
.
Критические точки второго рода:
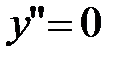 :
: 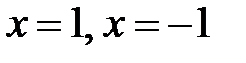 ;
;
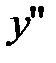 не существует: точек нет.
не существует: точек нет.
При переходе через точки 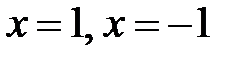 вторая производная
вторая производная 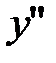 меняет знак.
меняет знак.
Þ 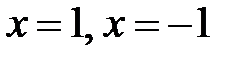 — точки перегиба.
— точки перегиба.
Асимптоты графика функции.
Определение: Прямая l называется асимптотой графика функции 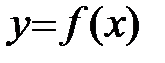 , если расстояние от точки М на графике до прямой l стремится к нулю при удалении точки М по графику функции от начала координат.
, если расстояние от точки М на графике до прямой l стремится к нулю при удалении точки М по графику функции от начала координат.
Асимптоты бывают вертикальные, горизонтальные, наклонные.
Вертикальной асимптотой называется прямая x=a, если 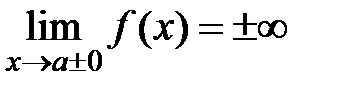 .
.
Находят вертикальную асимптоту по точкам разрыва второго рода (бесконечный разрыв).
Наклонной асимптотой называется асимптота, уравнение которой имеет вид: 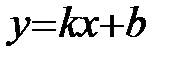 .
.
Оказывается, что если 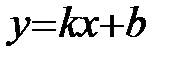 является асимптотой, то
является асимптотой, то 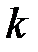 и
и 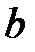 в уравнении определяются следующим образом
в уравнении определяются следующим образом 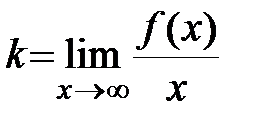 ,
, 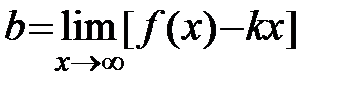 .
.
Доказательство:
| y |
| x |
| f(x) |
| kx+b |
| x |
| N |
| Q |
| M(x;y) |
| y=kx+b |
| асимптота |
| график функции |
По определению асимптоты: если ОМ 
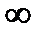 , то |MN|
, то |MN|  0.
0.
Þ |MQ|→0 при x→±∞, т.к. 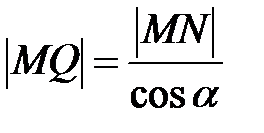 .
.
По чертежу: 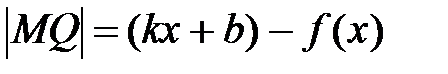 .
.
Перейдем к пределу при x→±∞:
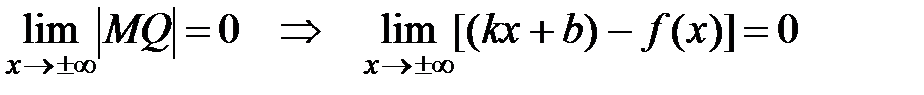 (*)
(*)
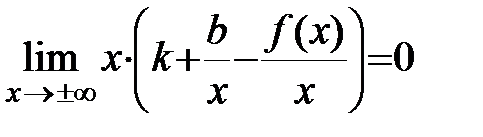
Þ 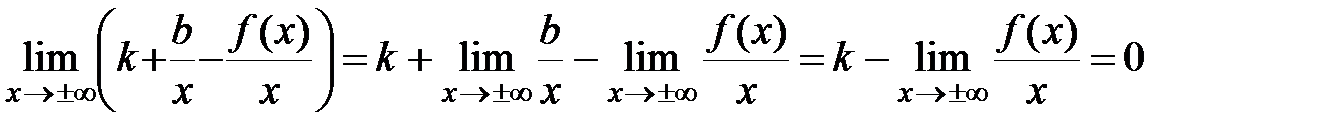 .
.
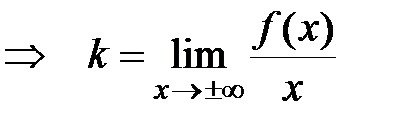 .
.
Из (*) Þ 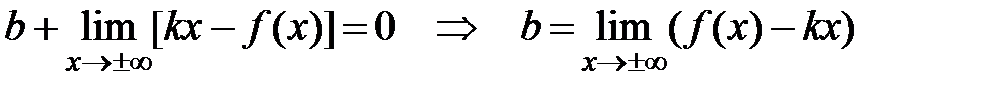 .
.
Ч.т.д.
Замечание 1: Чтобы у кривой были наклонные асимптоты, нужно, чтобы соответствующие пределы в определении k и b были конечными, причем предел при x→+∞ и предел при x→-∞ нужно вычислять отдельно.
Замечание 2: Если k=0, то y=b. Наклонная асимптота в этом случае называется горизонтальной.
Замечание 3: Кривая никогда не пересекает вертикальную асимптоту, а горизонтальные и наклонные асимптоты кривая может пересекать и даже бесконечное число раз.
Пример: Найти асимптоты графика функции 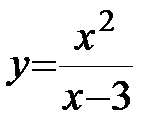 .
.
D(y): x¹3.
Þ x=3 – точка разрыва.
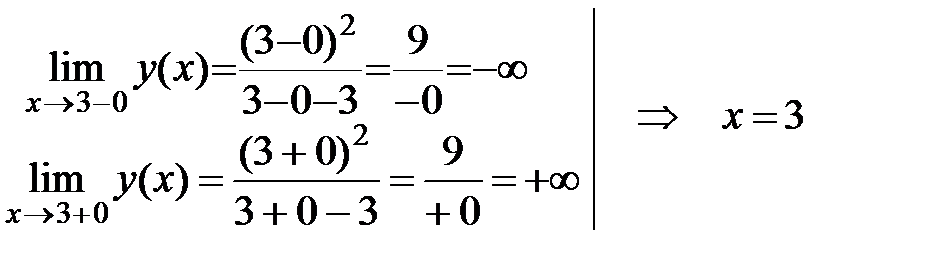 — вертикальная асимптота.
— вертикальная асимптота.
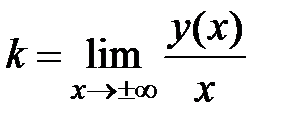 =
= 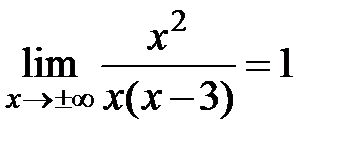 ;
;
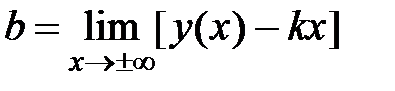 =
= 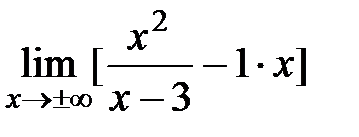 = =
= = 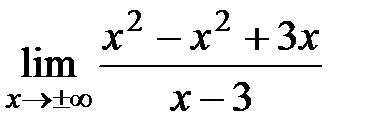 =3 Þ
=3 Þ 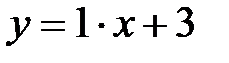 .
.
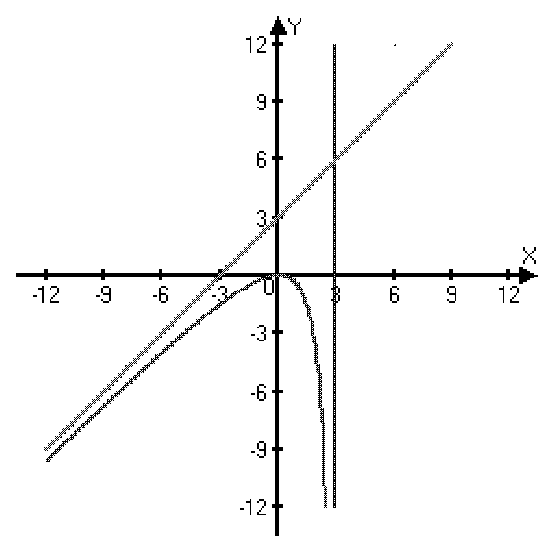
Þ 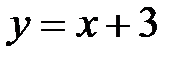 — наклонная асимптота.
— наклонная асимптота.
Схема полного исследования функции.
1. Определить естественную область D(y) определения функции.
2. Исследовать на четность и нечетность.
3. Найти точки пересечения графика функции с осями координат.
4. Найти асимптоты.
5. Найти интервалы возрастания и убывания функции, точки экстремума.
6. Найти интервалы выпуклости графика, точки перегиба.
7. Построить график функции.
Пример:
Провести полное исследование и построить график функции 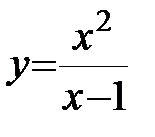 .
.
1. Область определения функции D(y): x¹1.
2. Т.к. область определения не симметрична относительно начала координат, то функция не является ни четной, ни нечетной.
3. Точки пересечения с 0x: y=0 Þ 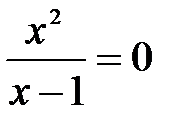 Þ x=0 Þ точка (0, 0) – точка пересечения с осями.
Þ x=0 Þ точка (0, 0) – точка пересечения с осями.
4. x=1 – точка разрыва.
Вертикальная асимптота:
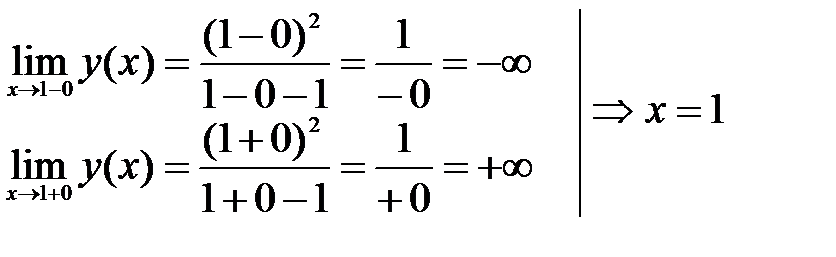 — вертикальная асимптота.
— вертикальная асимптота.
Наклонная асимптота: 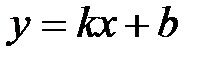 .
.
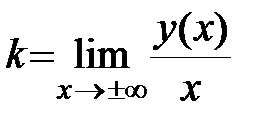 =
= 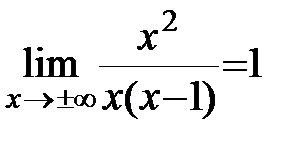 ;
;
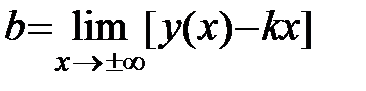 =
= 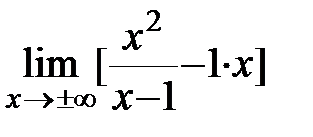 =
= 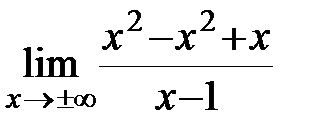 =1 Þ
=1 Þ 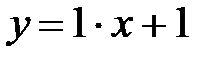 .
.
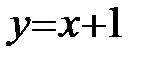 — наклонная асимптота.
— наклонная асимптота.
5. 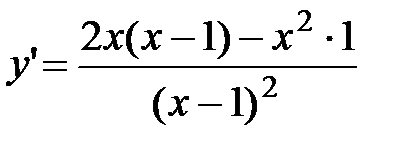 =
= 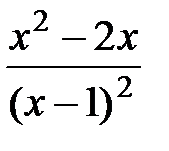 =
= 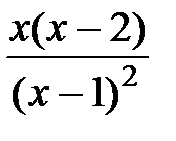 .
.
Критические точки: 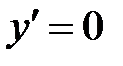 , т.е. числитель равен нулю Þ
, т.е. числитель равен нулю Þ 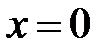 ,
, 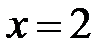 ;
;
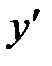 – не существует, т.е. знаменатель равен нулю Þ
– не существует, т.е. знаменатель равен нулю Þ 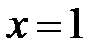 .
.
| x | (-∞;0) | x=0 | (0;1) | x=1 | (1;2) | x=2 | (2;+∞) |
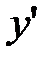
| + | − | не существует | − | + | ||
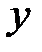
| возрастает | max y(0)=0 | убывает | не существует | убывает | min y(2)=4 | возрастает |
6. 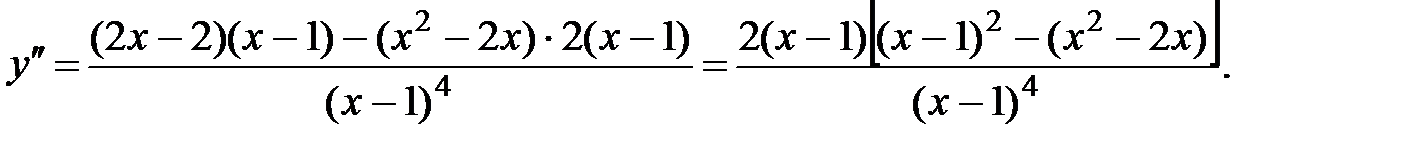
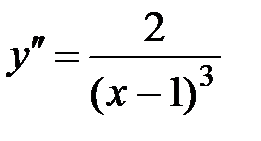 .
.
Критические точки второго рода:
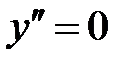 , т.е. числитель равен нулю Þ точек нет;
, т.е. числитель равен нулю Þ точек нет;
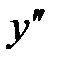 – не существует, т.е. знаменатель равен нулю Þ
– не существует, т.е. знаменатель равен нулю Þ 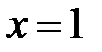 Þ точек перегиба нет, т.к. x=1ÏD(y).
Þ точек перегиба нет, т.к. x=1ÏD(y).
| x | (-∞;1) | x=1 | (1;+∞) |
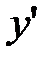
| − | не существует | + |
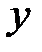
| вогнута | не существует | выпукла |
7. График функции:
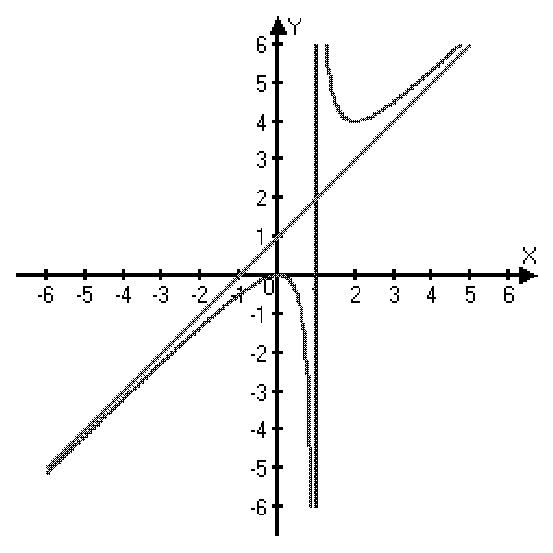
Дата добавления: 2016-06-05; просмотров: 1660;











