Разложение векторов по базису

Теперь мы готовы найти точное разложение векторов по базису для случая, если координаты всех векторов заданы в виде целых чисел или посредством обыкновенных дробей (рациональные числа).

Задание 4. Разложить по базису

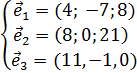
a) вектор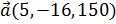

b) вектор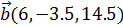

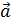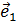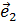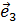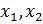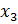Решение. Для того, чтобы найти разложение вектора по базису , , , необходимо найти коэффициенты и в уравнении:

.

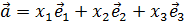Если теперь вместо каждого вектора подставить столбец его координат, то мы получим алгебраическую систему уравнений 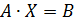с матрицами, составленными из столбцов координат соответствующих векторов. А именно:

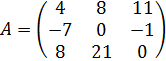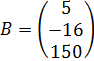, и .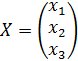

Поступая аналогично предыдущим вычислениям, образуем в Excel расширенную матрицу W и считываем ее в матрицы A и B:

# Работа с буфером обмена

Data <- read.table("clipboard", h=FALSE, dec=",", sep = "\t") # Чтение из буфера обмена excel-формата

W <- data.matrix(Data) # Объявить таблицу чисел матрицей в R

A <- W[ , 1:3]; A # Считываем матрицу A системы

B <- W[ , 4]; B # Считываем правый столбец системы

с результатом, представленным на рисунке 3

Рис. 3

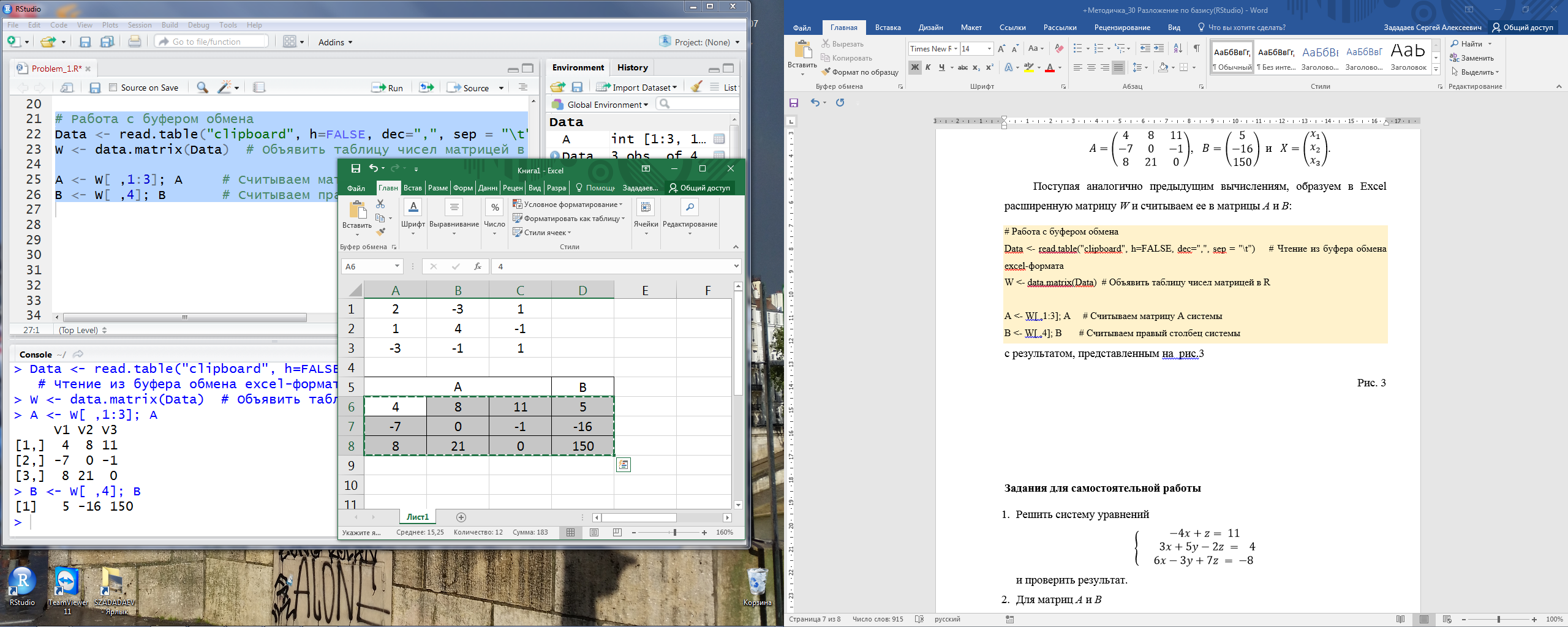
Далее остается запустить операцию решения системы:

solve(A, B) # Приближенно решаем систему AX=B

solve.bigq(A, B) # Точно решаем систему AX=B

с результатом для обоих случаев:

> solve(A, B) # Приближенно решаем систему AX=B

V1 V2 V3

3.0000000000000000 6.0000000000000000 -4.9999999999999991

> solve.bigq(A, B) # Точно решаем систему AX=B

Big Rational ('bigq') 3 x 1 matrix:

[,1]

[1,] 3

[2,] 6

[3,] -5

Таким образом, искомое разложение по базису принимает вид:

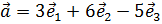
Аналогично, для вектора 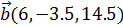получим:

B <- c(6, -3.5, 14.5); B

solve(A, B) # Приближенно решаем систему AX=B

solve.bigq(A, B) # Точно решаем систему AX=B

[1] 6.0 -3.5 14.5

> solve(A, B) # Приближенно решаем систему AX=B

V1 V2

5.0000000000000000e-01 5.0000000000000000e-01

V3

-2.0438670584833814e-17

> solve.bigq(A, B) # Точно решаем систему AX=B

Big Rational ('bigq') 3 x 1 matrix:

[,1]

[1,] 1/2

[2,] 1/2

[3,] 0

с ответом:

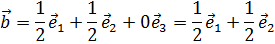
Заключение

Заметим, что если в координатах вектора указать обыкновенную дробь, например, для вектора 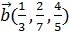запустив строку кода:

b <- c(1/3, 2/7, 4/5)

b

> b <- c(1/3, 2/7, 4/5);

> b

[1] 0.3333333 0.2857143 0.8000000

то последующее решение solve.bigq(A, b) уже не будет точным, т.к. дроби 1/3 и 2/7 успеют потерять точность после округления в десятичном представлении double-арифметики.

Для сохранения точности необходимо такой вектор 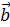изначально заявлять как bigq:

b <- c(as.bigq(1, 3), as.bigq(2, 7), as.bigq(4, 5))

b

> b <- c(as.bigq(1,3), as.bigq(2,7), as.bigq(4,5))

> b

Big Rational ('bigq') object of length 3:

[1] 1/3 2/7 4/5

Если же координаты вектора заданы как иррациональные числа, например, 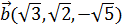, то ответом solve.bigq(A, b) станут обыкновенные дроби, наиболее близкие к истинным иррациональным результатам. То есть сам по себе ответ в виде обыкновенных дробей еще не говорит об абсолютной точности! Проверяйте результаты прямыми подстановками.

Замечание. Важно знать, что функция solve.bigq иногда отказывается работать с вполне хорошими невырожденными матрицами, ошибочно объявляя их вырожденными. В такие моменты всегда непосредственно проверяйте равенство нулю определителя det(A). В случае ошибки остается использовать лишь приближенное решение с помощью функции solve, которая с практической точки зрения ничем не уступает solve.bigq.

Впрочем, нет сомнений, что со временем подобная ошибка будет устранена авторами библиотеки.