Расширение double-арифметики

В данной части мы познакомимся с вычислениями в семантике обыкновенных дробей, которые позволяют сохранить точность результатов при оперировании с целыми или рациональными числами.

Алгебраически точное решение матричных уравнений*

В языке R разработана специальная библиотека gmp, которая позволяет оперировать не с десятичным форматом чисел, а с алгебраическим.

Поясним смысл сказанного, предварительно загрузив библиотеку gmp через меню Tools/Install Packages… и активировав ее кодом:

library(gmp) # Библиотека расширенных типов целых и рациональных чисел

Теперь попробуем продемонстрировать разницу между обычной double арифметикой as.numeric и расширенной с помощью специальных типов as.bigz и as.bigq.

Задание 1. Вычислить с максимальной точностью число .

Решение. Подключим максимальную выводимую на экран точность double арифметики:

options(digits = 22) # Выводим на экран консоли максимальное число разрядов

и вычислим число :

2^200

с результатом, записанным с помощью digits = 22 символов:

Это означает, что число мы представляем себе примерно, как:

–

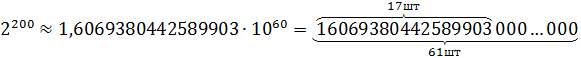число из 61 цифры, первые 17 из которых мы видим, как значащие.

А остальные 44 цифры, вместо которых стоят нули, чему равны? Ответить на это вопрос здесь невозможно, т.к. мы использовали обычную double арифметику, и памяти, выделяемой на такие числа, недостаточно для получения более точного ответа.

Попробуем теперь воспользоваться специальным типом данных bigz, который выделяет под такие вычисления практически неограниченную память в рамках физически доступной на каждом конкретном компьютере (bigz – дословно «большие целые»):

as.bigz(2^200) # Вычислить выражение со всеми значащими цифрами

as.bigz(2)^200 # То же самое

с абсолютно точным результатом:

в котором хорошо видны все 61 значащие цифры числа!

Далее прокомментируем идею абсолютной точности рациональных чисел в алгебраической форме, т.е. чисел, которые можно представить в виде несократимой дроби .

Потеря точности при вычислении таких дробей связана с возникновением периодических десятичных дробей, которые неизбежно приходится где-то обрывать. Однако, если результаты, включая промежуточные, представлять в виде обыкновенных дробей, то точность будет сохраняться – эту идею как раз и использует в своих алгоритмах специальный тип данных bigq (bigq – ­дословно «большие рациональные»).

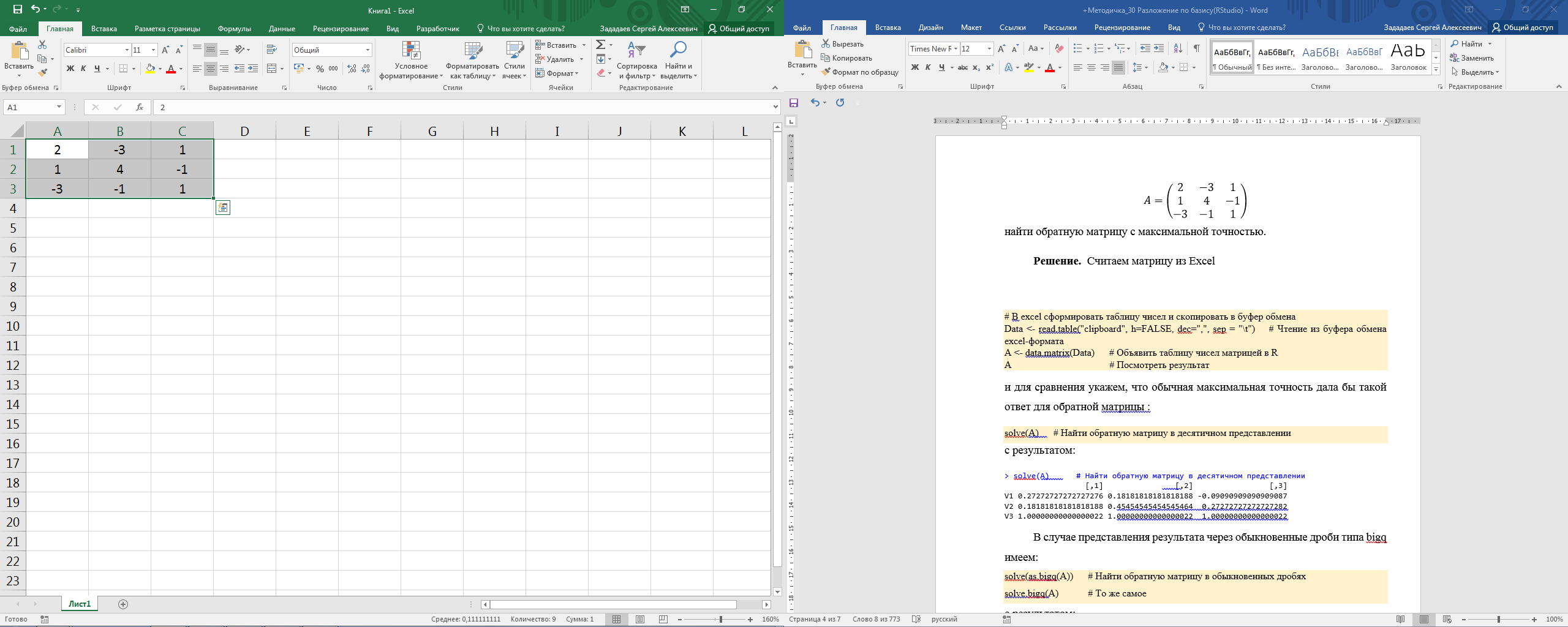
Задание 2. Для матрицы A

найти обратную матрицу с максимальной точностью.

Решение. Считаем матрицу из Excel (см. Рис.1)

Рис.1

# В excel сформировать таблицу чисел и скопировать в буфер обмена

Data <- read.table("clipboard", h=FALSE, dec=",", sep = "\t") # Чтение из буфера обмена excel-формата

A <- data.matrix(Data) # Объявить таблицу чисел матрицей в R

A # Посмотреть результат

и для сравнения укажем, что обычная максимальная точность double-арифметики дала бы такой ответ для обратной матрицы :

solve(A) # Найти обратную матрицу в десятичном представлении

с результатом:

В случае представления результата через обыкновенные дроби типа bigq имеем:

solve(as.bigq(A)) # Найти обратную матрицу в обыкновенных дробях

solve.bigq(A) # Tо же самое

с результатом:

Проверим, насколько точной получится единичная матрица 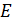, если перемножить :

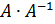A%*%solve(as.bigq(A)) # Проверка точности

с абсолютно точным результатом:

Задание 3. Решить систему уравнений

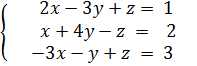
в обыкновенных дробях.

Решение. Матрица коэффициентов системы совпадает с матрицей A из предыдущего примера

,

а столбец правой части .

Для сравнения приводим два решения: приближенное и точное:

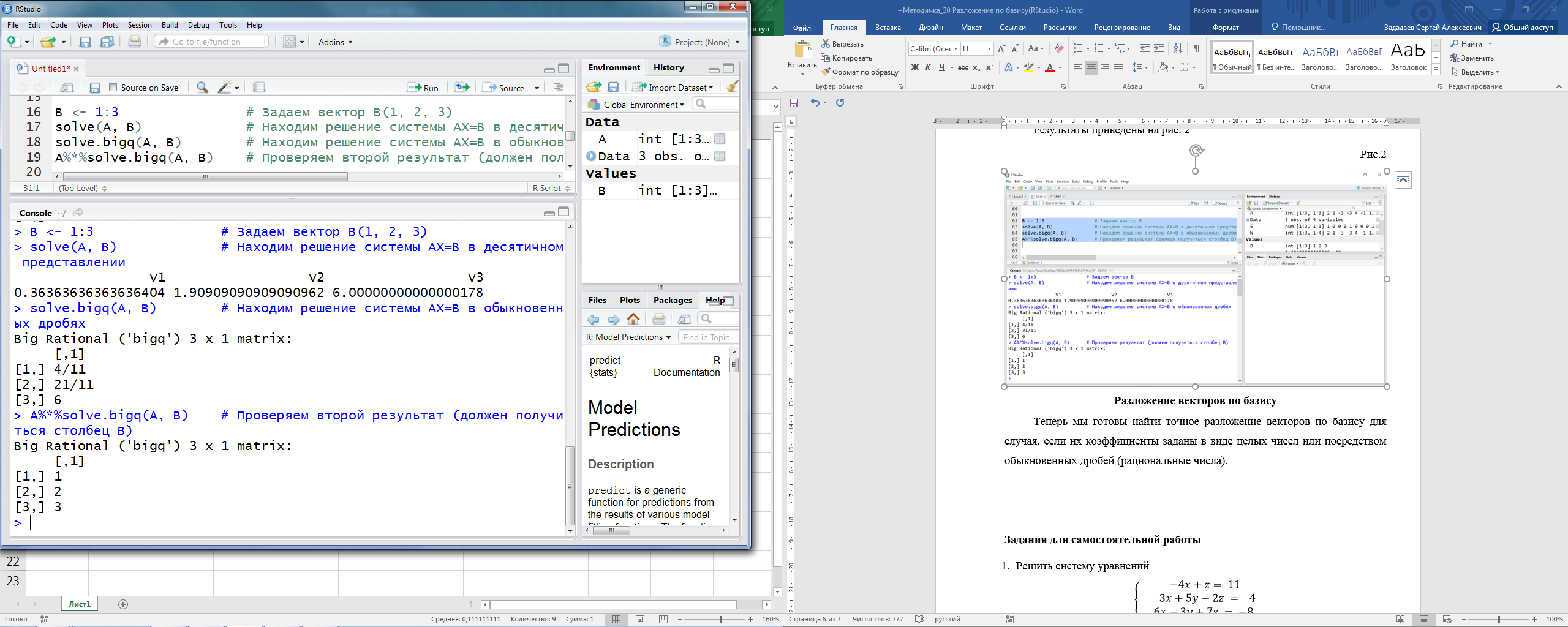
B <- 1:3 # Задаем вектор B(1, 2, 3)

solve(A, B) # Находим решение системы AX=B в десятичном представлении

solve.bigq(A, B) # Находим решение системы AX=B в обыкновенных дробях

A%*%solve.bigq(A, B) # Проверяем второй результат (должен получиться столбец B)

Результаты приведены на рис. 2

Рис.2