ОБЩИЙ МЕТОД ПОСТРОЕНИЯ ДОВЕРИТЕЛЬНЫХ ИНТЕРВАЛОВ

Метод позволяет по имеющейся случайной выборке построить функцию u(Θ, Θ*), распределенную асимптотически нормально с нулевым математическим ожиданием и единичной дисперсией. В основе метода лежат следующие положения. Пусть:

f(х, Θ*) – плотность распределения случайной величины Х;

ln [L(x, Θ*)] – логарифм функции правдоподобия;

;

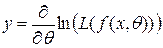σ² =М(Y)² – дисперсия Y.

Если математическое ожидание М(у)=0 и дисперсия Y конечна, то распределение случайной величины

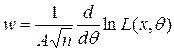
асимптотически нормально с параметрами 0 и 1 при n→∞.

Пример 4.1. Построить доверительный интервал с надежностью g =1– a для оценки m^*_x математического ожидания m_x случайной величины Х, имеющей экспоненциальное распределение с функцией плотности

f(x, λ) = λехр(–λ х).

Решение. Известно, что для экспоненциального закона распределения математическое ожидание m₁= 1/ λ, а дисперсия m₂= 1/ λ ₂. Обозначим через l оценку параметра λ. Определим оценку математического ожидания m^*_x, вспомогательную переменную у, производную от логарифма функции прачвдоподобия:

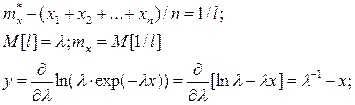
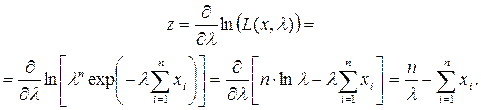
Оценка m^*_x параметра m_x является состоятельной и несмещенной, следовательно:

М[у]=М[l^–1 – х) = 0

и значение σ² = М(l^–1 – х)² =l^–2 конечно.

Тогда случайная величина

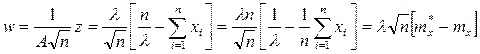
распределена нормально с параметрами 0 и 1.

Нормальное распределение симметрично, поэтому границы интервала следует выбрать симметрично относительно нулевой точки. Вероятность g= =1–a того, что модуль величины w не превысит некоторого заданного значения d, составит

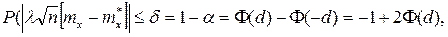
где Ф(d) – значение функции нормального распределения в точке d.

Величина d равна квантили u_1–a/2 стандартного нормального распределения уровня 1– a/2. Значение абсолютной погрешности оценивания

ε = | m_x – m^*_x| =d /(l_n^0,5) = u_{1– a/2} /(l_n^0,5).

Итак, имея достаточный объем выборки ЭД и задаваясь определенным уровнем надежности g можно определить доверительный интервал

θ₀ = m^*_x – ε, θ₁ = m^*_x + ε,

который с заданной вероятностью содержит неизвестный параметр m_x.

Аналогичные результаты для некоторых параметров распределения можно получить, используя более простые рассуждения.