Работа сельсинов в индикаторном режиме

Схема индикаторной связи приведена на рис. 5.4. Будем считать, что оба сельсина совершенно одинаковы и от одного датчика питается только один приемник.

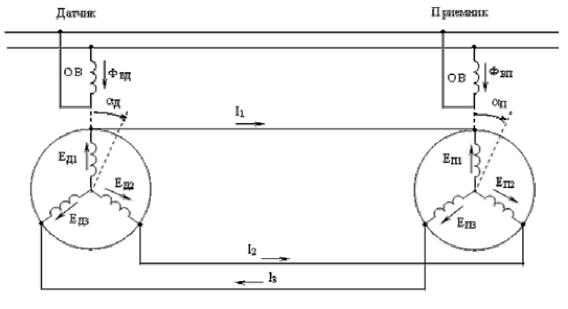
Рис. 5.4. Индикаторная схема «передачи угла»

При питании обмоток возбуждения датчика и приемника переменным током возникают пульсирующие потоки возбуждения Ф_вд и Ф_вп, которые индуцируют в обмотках синхронизации ЭДС (Е_д1 ,..., Е_п3). Величина каждой ЭДС зависит от углового положения соответствующей обмотки относительно оси поля возбуждения. Если принять гармонический закон распределения индукции магнитного поля, то:

; ;

; ;

; .

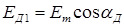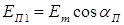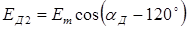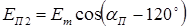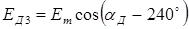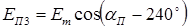Здесь 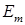– максимальное значение ЭДС, которое получается при соосном положении обмотки синхронизации и обмотки возбуждения. Из рис. 5.4 видно, что в любой момент времени ЭДС одноименных фаз датчика и приемника направлены встречно. Если сельсины находятся в согласованном положении, ЭДС одноименных фаз датчика и приемника равны по величине и уравновешивают друга.

При повороте датчика на угол a_д равенство ЭДС нарушается. По обмоткам синхронизации и линиям связи протекают токи, которые, взаимодействуя с потоками возбуждения, создают моменты, в равной мере действующие на вал датчика и приемника. Поскольку датчик обычно фиксируется, приемник будет поворачиваться в ту же сторону и на такой же угол, ибо только при согласованном положении ЭДС вновь будут уравновешивать друг друга. Найдем выражение синхронизирующего момента сельсинов.

Так как одноименные фазы датчика и приемника соединены встречно, то проходящий по ним ток:

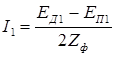
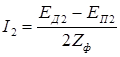
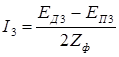
где 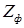– полное сопротивление обмотки синхронизации одного из сельсинов плюс половина сопротивления линии связи.

Подставляя значения ЭДС, учитывая, что

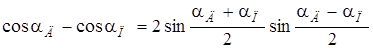
и обозначая разность углов поворота датчика и приемника a_д–a_п через угол рассогласования q, получим

,

,

.

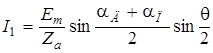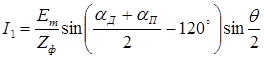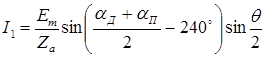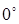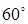Если один из сельсинов зафиксировать, а другой поворачивать на угол от до , то зависимость токов от угла рассогласования будет иметь вид, показанный на рис.5.5. Из формул токов и рис. 5.5 видно, что при любом угле рассогласования сельсинов сумма токов равна нулю. Поэтому в линиях связи отсутствует нулевой провод.

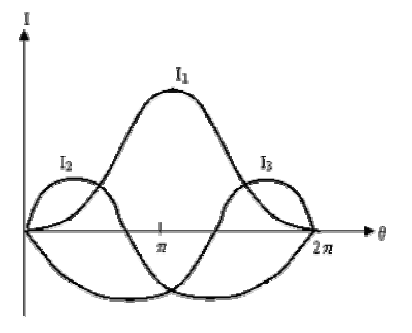
Рис.5.5. Зависимость токов в обмотках синхронизации в функции угла рассогласования

МДС ротора

Токи, протекая по обмоткам синхронизации, создают намагничивающие силы (НС) отдельных фаз, например (на пару полюсов). Эти силы складываясь,

образуют результирующие НС датчика и приемника.

Найдем их проекции на оси d и q. Например, для приемника это будет (рис. 5.6)

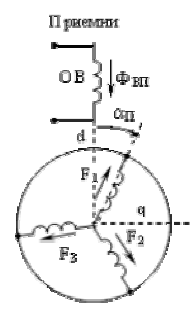
Рис. 25.1. Составляющие НС приемника

После подстановки значений НС и преобразований, получим:

;

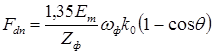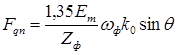
Продольная составляющая НС F_dп направлена встречно потоку возбуждения и пытается размагнитить сельсин. Однако ее действие компенсируется увеличением тока возбуждения так, что при малых углах рассогласования, при которых обычно и работают сельсины, ею можно пренебречь.

К тому же, значение F_dп много меньше F_qп. Например, при q = 50 F_dп/F_qп = 0, 026.

Поперечная составляющая НС F_qп , взаимодействуя с потоком обмотки возбуждения Ф_вп, создает вращающий момент, который можно определить подобно тому, как это делается для асинхронного двигателя.

.

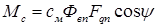Здесь 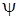– угол сдвига во времени между потоком возбуждения и током ротора (рис. 5.7). С учетом 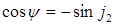, опуская знак минус, получим

(5.1)

Подставляя значение F_qп в (5.1), получим

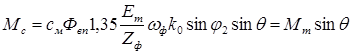, (5.2)

где М_m – максимальный синхронизирующий момент

.

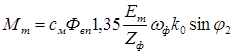Формула (5.2) показывает гармоническую зависимость момента синхронизации от угла рассогласования и, казалось бы, что сельсин имеет два устойчивых положения: пр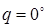и и 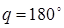. Однако положение при 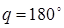– положение неустойчивого равновесия. Достаточно малейшего возмущения, чтобы сельсин из положения 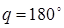перешел в положение 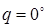. Аналогом этому может служить модель, состоящая из двух магнитов (рис. 5.8).

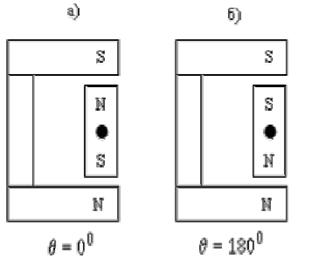
Рис. 25.2

Гармоническая зависимость (5.2) справедлива только при малых углах рассогласования q (порядка 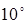÷ 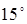). При больших углах необходимо учитывать размагничивающее действие продольной составляющей результирующей НС обмоток синхронизации F_d, соотношения индуктивных сопротивлений обмоток по продольной – х_d и поперечной – х_q осям и ряд других факторов.

На рис. 5.9 даны характерные графики М_c=f(q) для сельсина неявнополюсной (1) и явнополюсной (2) конструкции. В первой из них x_d= x_q во второй x_d > x_q.