Полюсное управление исполнительным двигателем
Схема управления приведена на рис. 2.4 Напряжение управления подается на обмотку главных полюсов, напряжение возбуждения – на обмотку якоря, по которой в течение всего времени работы двигателя протекает ток возбуждения. В двигателях, мощностью более 10 Вт, для его ограничения включают дополнительное сопротивление  .
.
Если пренебречь насыщением магнитной цепь, можно считать 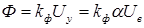 . Тогда ток якоря
. Тогда ток якоря
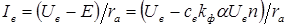
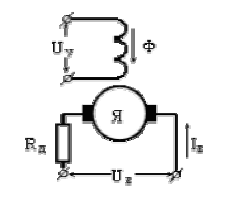
Рис. 17.4. Схема включения исполнительного двигателя при полюсном управлении
Вращающий момент
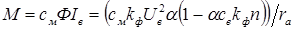
Принимая за базовый момент пусковой ( 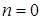 ,
, 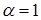 )
)
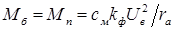
получим относительное значение момента
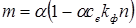
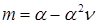
С учетом (17.2) уравнение механической характеристики примет вид
Решив его относительно 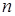 , получим уравнение регулировочной характеристики
, получим уравнение регулировочной характеристики
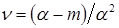
Механическая мощность в относительных единицах 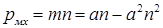 . Скорость, при которой наступает максимум мощности
. Скорость, при которой наступает максимум мощности 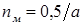 . Тогда максимальная механическая мощность будет
. Тогда максимальная механическая мощность будет
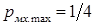
Мощность управления
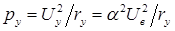
Мощность возбуждения 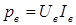 . Подставляя значение тока, получим
. Подставляя значение тока, получим

На рис. 17.5,а представлены механические, на рис. 17.5,б – регулировочные характеристики, а на рис. 17.6 показана зависимость  исполнительного двигателя при полюсном управлении.
исполнительного двигателя при полюсном управлении.
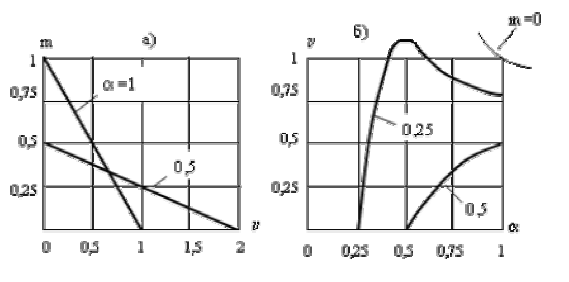
Рис.17.5. Механические (а) и регулировочные (б) характеристики исполнительного
двигателя постоянного тока при полюсном управлении
Проанализируем эти графики.
Механические характеристики линейные, но непараллельные, к тому же и неоднозначные (одну и ту же частоту вращения можно получить при разных значениях a). Пусковой момент прямо–, а частота вращения холостого хода обратно пропорциональны коэффициенту сигнала и при малых a может существенно превышать номинальную, что безусловно опасно для двигателя.
Регулировочные характеристики нелинейные, а при 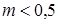 неоднозначные. По этой причине полюсное управление используют лишь при
неоднозначные. По этой причине полюсное управление используют лишь при 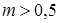 .
.
Мощность управления пропорциональна квадрату коэффициента сигнала и не зависит от частоты вращения. Она значительно меньше, чем при якорном управлении, что является достоинством данного способа.
Мощность возбуждения с увеличением частоты вращения уменьшается и тем быстрее, чем больше 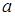 .
.
Максимум механической мощности не зависит от коэффициента сигнала, что также можно отнести к достоинствам полюсного управления.
Несмотря на отмеченные достоинства полюсного управления, предпочтение все–таки следует отдать якорному потому, что оно обеспечивает линейные и однозначные характеристики, в принципе исключает самоход (при полюсном он возможен из–за взаимодействия тока якоря с потоком остаточной намагниченности полюсов), обладает более высоким быстродействием, поскольку индуктивность якоря меньше индуктивности обмотки возбуждения.
18. Полюсное управление исполнительным
двигателем
Амплитудное управление. Поскольку в этом способе векторы напряжения 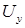 ,
, 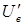 перпендикулярны,
перпендикулярны,  . Уравнения (1.3) и (1.4) принимают вид
. Уравнения (1.3) и (1.4) принимают вид
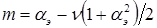 (1.5)
(1.5)
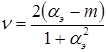 (1.6)
(1.6)
По данным уравнениям на рис.1.6,а построены механические/ 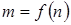 при
при  , а на рис.1.6,б регулировочные/
, а на рис.1.6,б регулировочные/ 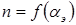 при
при 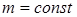 / характеристики идеального асинхронного исполнительного двигателя при амплитудном управлении.
/ характеристики идеального асинхронного исполнительного двигателя при амплитудном управлении.

Рис.1.6. Механические (а) и регулировочные (б) характеристики асинхронного исполнительного двигателя при амплитудном управлении
__________ – идеального АИД; ––––––––– – реального АИД.
Анализ механических характеристик позволяет сделать следующие выводы:
1)Механические характеристики идеального двигателя линейные, но не параллельные, что свидетельствует о зависимости быстродействия от коэффициента сигнала (см. § 1.3);
2) Максимальный момент двигатель развивает при пуске. В относительных единицах он равен коэффициенту сигнала 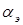 ;
;
3) При 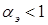 скорость теоретического холостого хода всегда меньше синхронной, что объясняется действием токов обратной последовательности, которые создают тормозные моменты.
скорость теоретического холостого хода всегда меньше синхронной, что объясняется действием токов обратной последовательности, которые создают тормозные моменты.
Анализ регулировочных характеристик показывает:
1) Даже для идеального исполнительного двигателя они, к сожалению, нелинейные. Лишь при сравнительно небольших коэффициентах сигнала можно выделить зону пропорционального регулирования;
2) Напряжение трогания пропорционально моменту сопротивления.
Механическая мощность. В относительных единицах механическая мощность
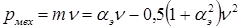 (1.7)
(1.7)
Максимум механической мощности найдем из уравнения
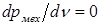
или
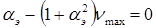
откуда
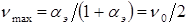
Следовательно, максимальную механическую мощность двигатель развивает при скорости, равной половине скорости холостого хода. Подставляя 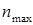 в (1.7), получим максимальное значение механической мощности
в (1.7), получим максимальное значение механической мощности
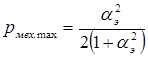
На рис. 1.7. показаны зависимости  при
при  . Из графиков видно, что даже при
. Из графиков видно, что даже при 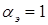 максимум механической мощности не превышает 1/4 базового значения; с уменьшением коэффициента сигнала использование двигателя ухудшается.
максимум механической мощности не превышает 1/4 базового значения; с уменьшением коэффициента сигнала использование двигателя ухудшается.
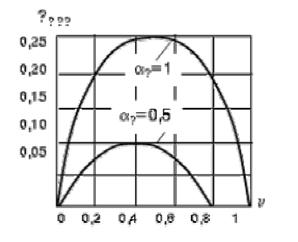
Рис. 1.7. Зависимость механической мощности от скорости вращения
при амплитудном управлении
Характеристики реального двигателя при амплитудном управлении должны определяться по полным схемам замещения, позволяющим учитывать реактивные сопротивления, намагничивающий ток, падения напряжения в обмотках, что конечно усложняет их вывод. Поэтому, не вдаваясь в детали, отметим лишь некоторые особенности реальных исполнительных двигателей.
Механические и регулировочные характеристики двигателей показаны пунктирными линиями на рис.1.6,а и 1.6,б. Как видно из рисунков, все они нелинейные и проходят выше характеристик идеального двигателя.
Однако выводы, сделанные выше относительно быстродействия, пропорциональности пускового момента и пр., остаются справедливыми и здесь.
Мощность возбуждения.  .В реальном двигателе намагничивающий ток, не учитываемый в идеальном, составляет 85¸ 90 % от номинального. В результате ток и мощность возбуждения остаются практически постоянными в любом режиме работы при всех значения
.В реальном двигателе намагничивающий ток, не учитываемый в идеальном, составляет 85¸ 90 % от номинального. В результате ток и мощность возбуждения остаются практически постоянными в любом режиме работы при всех значения 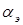 и
и 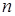 .
.
Мощность управления. 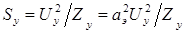 . Видно, что она в сильной мере зависит от коэффициента сигнала и немного от частоты вращения (от частоты вращения зависит
. Видно, что она в сильной мере зависит от коэффициента сигнала и немного от частоты вращения (от частоты вращения зависит 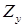 – полное сопротивление обмотки управления).
– полное сопротивление обмотки управления).
Фазовое управление. В этом случае векторы напряжения возбуждения 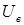 и управления
и управления 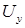 равны по величине, поэтому
равны по величине, поэтому 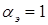 . Уравнения (1.3) и (1.4) принимают вид
. Уравнения (1.3) и (1.4) принимают вид
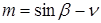 (1.8)
(1.8)
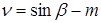 (1.9)
(1.9)
На рис. 1.8,а и б приведено семейство механических / 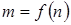 при
при 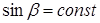 / и регулировочных /
/ и регулировочных / 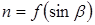 при
при 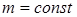 / характеристик идеального асинхронного исполнительного двигателя при фазовом управлении. Как видно из графиков, механические характеристики линейны и параллельны, что означает не зависимость быстродействия от коэффициента сигнала
/ характеристик идеального асинхронного исполнительного двигателя при фазовом управлении. Как видно из графиков, механические характеристики линейны и параллельны, что означает не зависимость быстродействия от коэффициента сигнала  .
.
Обратите внимание, что при коэффициенте сигнала меньшем единицы, теоретическая скорость холостого хода здесь меньше, чем при амплитудном управлении. Объясняется это большим значением тока обратной последовательности /проанализируйте формулы (1.2) при 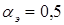 и
и 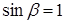 , что соответствует амплитудному управлению, а затем при
, что соответствует амплитудному управлению, а затем при  и
и 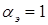 , что соответствует фазовому управлению/.
, что соответствует фазовому управлению/.
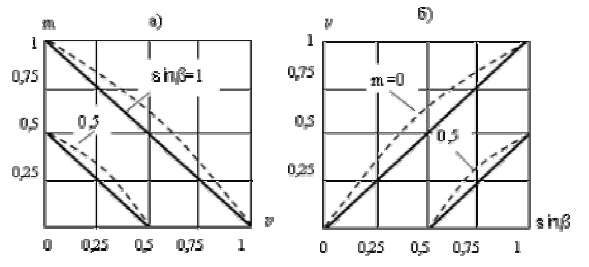
Рис.1.8. . Механические (а) и регулировочные (б) характеристики асинхронного исполнительного двигателя при фазовом управлении
__________ – идеального АИД; ––––––––– – реального АИД
К положительным качествам фазового управления следует отнести линейность регулировочных характеристик идеального двигателя. Механические и регулировочные характеристики реального двигателя конечно нелинейные, однако, их нелинейность весьма не большая (см. пунктирные графики на рис. 1.8, а и б).
Полная мощность возбужденияреального двигателя здесь, как и при амплитудном управлении, остается практически постоянной в широком диапазоне изменения скоростей и коэффициентов сигнала.
Полная мощность управленияне 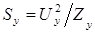 зависит от коэффициента сигнала, а зависит лишь от частоты вращения
зависит от коэффициента сигнала, а зависит лишь от частоты вращения 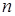 .
.
Механическая мощностьв относительных единицах равна
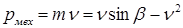 .
.
Относительную скорость, при которой наступает максимум мощности, найдем из условия 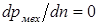 . Выполнив дифференцирование, получим
. Выполнив дифференцирование, получим 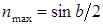 . С учетом последнего максимальная механическая мощность
. С учетом последнего максимальная механическая мощность
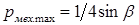
На рис. 1.12 построены графики 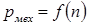 при
при 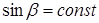 . Как и при амплитудном управлении, максимум механической мощности при фазовом управлении и
. Как и при амплитудном управлении, максимум механической мощности при фазовом управлении и 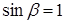 не превышает 1/4 базовой мощности.
не превышает 1/4 базовой мощности.
Рис. 1.9. Зависимость механической мощности от скорости вращения при фазовом
управлении
Конденсаторное управление. Известно, что при конденсаторном управлении коэффициент сигнала 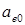 и емкость конденсатора
и емкость конденсатора 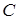 выбирают из условия получения кругового поля при пуске двигателя. Найдем эти значения.
выбирают из условия получения кругового поля при пуске двигателя. Найдем эти значения.
При круговом поле существуют только токи прямой последовательности, причем
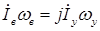
или
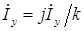 (1.10)
(1.10)
Токи в обмотках возбуждения и управления
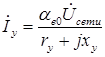 ;
; 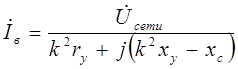 ,
,
где: 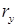 и
и 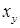 – активное и реактивное сопротивление схемы замещения двигателя для фазы управления при пуске двигателя (режим КЗ);
– активное и реактивное сопротивление схемы замещения двигателя для фазы управления при пуске двигателя (режим КЗ); 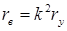 и
и 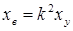 – то же для фазы возбуждения.
– то же для фазы возбуждения.
Подставляя значения токов в (1.10), получим
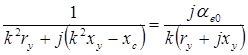
или
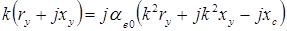
Приравнивая действительные и мнимые части,
 ;
; 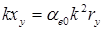
получим условия, необходимые для создания кругового поля:
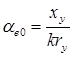 ;
; 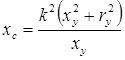 ;
; 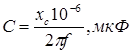
В общем случае аналитические выражения напряжений, токов и моментов при этом способе управления получаются весьма сложными и малопригодными для анализа. Поэтому ограничимся простым изображением механических 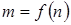 при
при 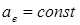 рис. 1.10,а и регулировочных /
рис. 1.10,а и регулировочных / 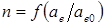 при
при 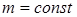 (рис. 1.10,б) характеристик реального асинхронного исполнительного двигателя [1]
(рис. 1.10,б) характеристик реального асинхронного исполнительного двигателя [1]
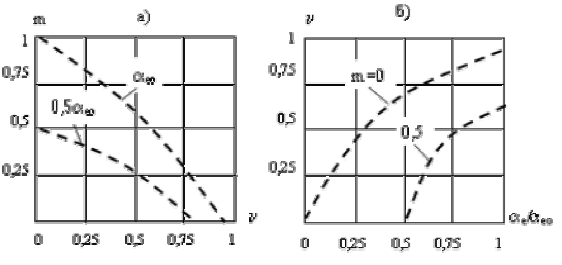
Рис.1.10. Механические (а) и регулировочные (б) характеристики реального асинхронного
исполнительного двигателя при конденсаторном управлении
Как видно из графиков, характеристики очень похожи на характеристики при амплитудном управлении. Это объясняется малым изменением фазы 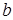 по сравнению с изменением амплитуды напряжения управления
по сравнению с изменением амплитуды напряжения управления 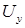 . Однако отличие есть и оно заключается в том, что теоретическая скорость холостого хода при
. Однако отличие есть и оно заключается в том, что теоретическая скорость холостого хода при 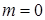 и
и 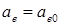 меньше синхронной. Причина этого – в эллиптичности магнитного поля, создающего не только движущие, но и тормозящие моменты. Напомним, что при конденсаторном управлении круговое поле имеет место только в пусковом режиме и
меньше синхронной. Причина этого – в эллиптичности магнитного поля, создающего не только движущие, но и тормозящие моменты. Напомним, что при конденсаторном управлении круговое поле имеет место только в пусковом режиме и 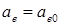 .
.
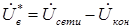 ,
,
При малых и средних скоростях вращения момент при конденсаторном управлении имеет большее значение, чем при других способах, что объясняется увеличением напряжения на обмотке возбуждения 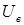 и соответственно увеличением магнитного потока машины.
и соответственно увеличением магнитного потока машины.
Напряжение увеличивается потому, что по мере разгона двигателя уменьшается ток возбуждения 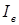 и уменьшается падение напряжения на конденсаторе, ибо
и уменьшается падение напряжения на конденсаторе, ибо 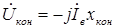 .
.
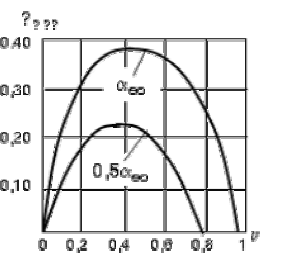
Рис. 1.11. Зависимость механической мощности от скорости вращения при конденсаторном управлении
Этим же фактом объясняется и большая величина максимальной механической мощности (рис. 1.11).
Полная мощность возбужденияс увеличением скорости вращения увеличивается, а мощность управленияуменьшается. Перераспределение мощностей поступающих от усилителя (мощность управления) и из сети (мощность возбуждения) позволяет на практике уменьшить мощность управления, что выгодно отличает данный способ управления от других.
В заключение этого раздела подведем некоторые итоги.
1. Механические характеристики АИД при всех способах управления нелинейные. Степень нелинейности оценивается максимальным расхождением 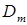 между действительной характеристикой и прямой, проведенной через точки холостого хода и короткого замыкания. На практике, чтобы найти
между действительной характеристикой и прямой, проведенной через точки холостого хода и короткого замыкания. На практике, чтобы найти 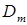 , параллельно линии, соединяющей точки ХХ и КЗ, проводят касательную к характеристике и из точки касания опускают перпендикуляр на ось абсцисс. Численное значение отрезка
, параллельно линии, соединяющей точки ХХ и КЗ, проводят касательную к характеристике и из точки касания опускают перпендикуляр на ось абсцисс. Численное значение отрезка 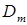 и будет нелинейностью механической характеристики (рис. 1.12,а)
и будет нелинейностью механической характеристики (рис. 1.12,а)
Уменьшить нелинейность можно увеличением активного сопротивления ротора, но это приводит к ухудшению использования АИД, поэтому нелинейность порядка 10% считается допустимой.
Наибольшую линейность имеют характеристики при фазовом способе управления, наименьшую – при конденсаторном управлении.
2. Регулировочные характеристики при всех способах управления так же нелинейные. Лишь при небольших значения 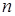 (порядка 0÷0,25) можно выделить более иле менее линейные участки характеристик, т.е. выделить зоны пропорционального регулирования.
(порядка 0÷0,25) можно выделить более иле менее линейные участки характеристик, т.е. выделить зоны пропорционального регулирования.
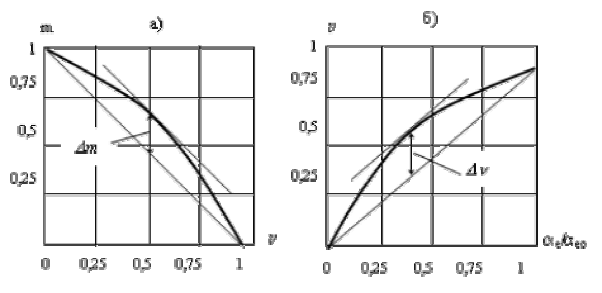
Рис.1.12. Определение степени нелинейности механических (а) и регулировочные (б)
характеристик реального асинхронного исполнительного двигателя
С целью расширения этой зоны в абсолютном значении скоростей вращения, целесообразно использовать двухполюсные АИД, рассчитанные на повышенную частоту питающей сети, т.к.  , где
, где 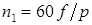 .
.
Количественно степень нелинейности регулировочных характеристик определятся подобно тому, как это делается для механических характеристик (рис. 1.12,б). Наиболее линейные характеристики при фазовом, наименее линейные при конденсаторном управлении.
И хотя конденсаторное управление имеет наименее линейные характеристики, этот способ получил широкое распространение, благодаря простоте реализации.
19. Динамические свойства асинхронных
исполнительных двигателей
Одним из главных требований, предъявляемых к исполнительным двигателям, является требование высокого быстродействия, под которым понимают способность двигателя достигать заданной частоты вращения за максимально короткое время.
Быстродействие определяется скоростью протекания электромагнитных и электромеханических переходных процессов, возникающих в двигателе при подаче сигнала управления.
Как известно, скорость затухания переходных процессов зависит от постоянных времени – электромагнитной и электромеханической. Благодаря большому активному сопротивлению ротора, электромагнитная постоянная времени  становится на порядок меньше электромеханической. Поэтому электромагнитными переходными процессами здесь можно пренебречь и считать, что быстродействие исполнительного двигателя определяется только электромеханической постоянной времени. Последнюю найдем из уравнения движения при пуске двигателя вхолостую
становится на порядок меньше электромеханической. Поэтому электромагнитными переходными процессами здесь можно пренебречь и считать, что быстродействие исполнительного двигателя определяется только электромеханической постоянной времени. Последнюю найдем из уравнения движения при пуске двигателя вхолостую 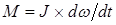 . Здесь
. Здесь 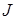 – момент инерции вращающихся частей.
– момент инерции вращающихся частей.
Механические характеристики идеального асинхронного исполнительного двигателя линейные, что позволяет описать их одной формулой 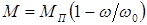 , где
, где 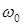 и
и 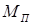 – угловая скорость холостого хода и пусковой момент. Подставив эту формулу в уравнение движения и решив его относительно
– угловая скорость холостого хода и пусковой момент. Подставив эту формулу в уравнение движения и решив его относительно 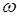 , получим
, получим

где 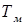 – электромеханическая постоянная, времени
– электромеханическая постоянная, времени
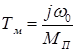 (1.11)
(1.11)
На рис. 1.13 показана кривая разгона двигателя, из которой видно, что угловая скорость вращения асимптотически приближается к установившемуся значению 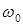 . При
. При 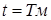 угловая скорость вращения
угловая скорость вращения 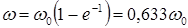 . Следовательно, постоянную
. Следовательно, постоянную 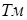 можно рассматривать как время разгона двигателя до скорости, соответствующей
можно рассматривать как время разгона двигателя до скорости, соответствующей 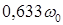 .
.
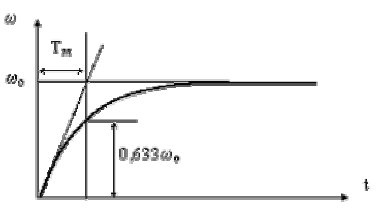
Рис. 1.13. Кривая разгона двигателя при пуске в холостую
При амплитудном управлении механические характеристики непараллельные, т.е. пусковой момент пропорционален коэффициенту сигнала 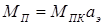 , где
, где 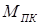 – пусковой момент при круговом поле, а угловая скорость идеального холостого хода – не пропорциональна
– пусковой момент при круговом поле, а угловая скорость идеального холостого хода – не пропорциональна 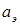 . Ее значение найдем из (1.6), положив
. Ее значение найдем из (1.6), положив 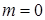
 .
.
Подставим эти значения 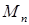 и
и 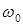 в (1.11), получим
в (1.11), получим
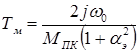 .
.

Из этой формулы видно, что с уменьшением коэффициента сигнала, электромеханическая постоянная времени растет, а это значит – быстродействие исполнительного двигателя ухудшается. Сказанное относится и к конденсаторному управлению, чьи характеристики похожи на характеристики при амплитудном управлении.
При фазовом управлении механические характеристики параллельные, т.е. пусковой момент и угловая скорость холостого хода изменяются пропорционально коэффициенту сигнала ( 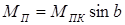 ,
, 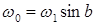 ). В этом случае электромеханическая постоянная времени будет
). В этом случае электромеханическая постоянная времени будет
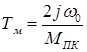 ,
,
т.е. при фазовом управлении постоянная времени и быстродействие не зависят от коэффициента сигнала.
Так как механические характеристики реальных двигателей проходят выше идеальных, постоянные времени реальных двигателей всегда получаются немного меньше идеальных. Однако сказанное выше относительно влияния коэффициента сигнала на быстродействие остается справедливым и здесь.
В выражения постоянных времени входит значение угловой скорости вращения 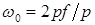 ,
,
следовательно, на величину 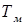 влияет частота сети и число пар полюсов машины. По этой причине двигатели, рассчитанные на повышенную частоту, имеют большую постоянную времени и худшее быстродействие, чем двигатели, спроектированные на частоту 50 Гц (см. табл.1).
влияет частота сети и число пар полюсов машины. По этой причине двигатели, рассчитанные на повышенную частоту, имеют большую постоянную времени и худшее быстродействие, чем двигатели, спроектированные на частоту 50 Гц (см. табл.1).
Таблица1. Электромеханические постоянные времени асинхронных исполнительных двигателей
| Тип двигателя | 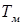 , с , с
| |
| 50 Гц | 400 Гц | |
| АИД с полым немагнитным ротором | 0,005¸ 0,05 | 0,015¸ 0,10 |
| АИД с полым ферромагнитным ротором | 0,200¸ 1,00 | 0,300¸ 3,00 |
| АИД с ротором «беличья клетка» | 0,020¸ 0,10 | 0,050¸ 0,15 |
Дата добавления: 2022-02-05; просмотров: 532;











