АСИНХРОННЫЕ ИСПОЛНИТЕЛЬНЫЕ ДВИГАТЕЛИ

Общие сведения

Асинхронные исполнительные двигатели это двухфазные двигатели с двумя обмотками на статоре, сдвинутыми в пространстве на 90 электрических градусов (рис.1.1). Для того чтобы обмотки создавали вращающееся магнитное поле, необходим временной сдвиг токов в этих обмотках. В зависимости от способа сдвига токов различают три способа управления исполнительными двигателями: амплитудный (рис.1.1,а); фазовый (рис.1.1,б) и амплитудно–фазовый (рис.1.1,в).

При амплитудном управлении на обмотку возбуждения подается напряжение 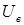, а на обмотку управления – напряжение 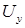, переменное по амплитуде и сдвинутое по фазе относительно него на 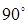. Управление двигателем осуществляется изменением величины напряжения 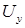. Отношение напряжения управления 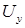к напряжению возбуждения 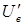, приведенному к числу витков обмотки управления, называют эффективным коэффициентом сигнала

,

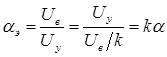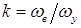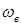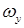где – коэффициент трансформации; и – эффективные числа витков обмоток возбуждения и управления; 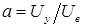– коэффициент сигнала.

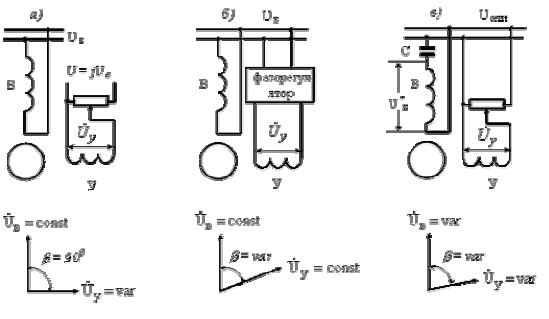
Рис.1.1. Способы управления асинхронным исполнительным двигателем

Круговое магнитное поле и максимальная частота вращения имеют место только при 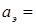1. При 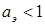– поле эллиптическое, а частота вращения меньше максимальной. При 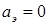– поле пульсирующее; двигатель не вращается. Реверс двигателя осуществляется за счет изменения фазы напряжения управления.

При фазовом управлении на обмотку возбуждения подается напряжение сети 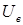, а на обмотку управления – постоянное по амплитуде напряжение, величина которого равна приведенному напряжению возбуждения 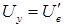, 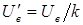. Регулирование частоты вращения осуществляется изменением фазы напряжения управления. За коэффициент сигнала здесь принимается 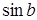. И вновь: при поле круговое, частота вращения максимальная; при 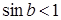поле эллиптическое, частота вращения меньше максимальной. При 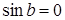поле пульсирует, частота вращения равна нулю. При 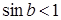двигатель изменяет направление вращения.

Амплитудно–фазовое управление чаще всего реализуется как конденсаторное. На первый взгляд этот способ кажется амплитудным, однако, это не так. Дело в том, что при изменении амплитуды напряжения управления 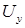, изменяется частота вращения двигателя 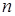, изменяется ток возбуждения 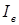, а поскольку напряжение на обмотке возбуждения 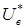равно разности напряжения сети 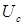и падения напряжения на конденсаторе 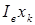, то оно изменяется как по величине, так и по фазе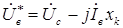

Коэффициентом сигнала 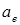здесь принято называть отношение напряжения управления 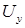к напряжению сети : .

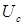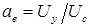Известно, что характеристики конденсаторного двигателя во многом зависят от того, как выбраны соотношения напряжений на обмотках и емкость конденсатора. Обычно их выбирают из условия получения кругового магнитного поля при пуске двигателя. Коэффициент сигнала, обеспечивающий это условие, обозначают 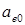. Поэтому при 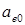поле круговое, при 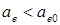– эллиптическое, при 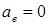– пульсирующее.

Анализируя сказанное выше, можно сделать вывод, что несмотря на конструктивные различия способов управления асинхронным исполнительным двигателем, их объединяет общая идея управления: деформация магнитного поля от кругового к эллиптическому до пульсирующего.

Для обеспечения устойчивой работы двигателя во всем диапазоне частот вращения, для расширения зоны регулирования и, как узнаем из дальнейшего, для устранения самохода, асинхронные исполнительные двигатели изготавливают с роторами, имеющими большие активные сопротивления (рис. 1.2). В результате их критические скольжения всегда больше единицы (кривая 1). У обычных машин 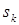= 0,1¸ 0,5 (кривая 2).

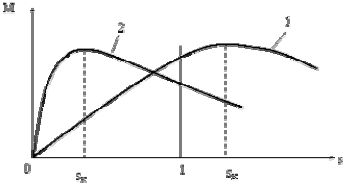
Рис.1.2. Механические характеристики исполнительных (1) и силовых (2)
асинхронных двигателей

Большие сопротивления ротора приводят к увеличению потерь и снижению механической мощности. Поэтому асинхронные исполнительные двигатели имеют полезную мощность в 2¸ 3 раза меньшую, чем силовые двигатели такого же габарита.

16.2. Уравнения токов и схемы замещения асинхронных исполнительных
двигателей

В общем случае асинхронный исполнительный двигатель является несимметричной двухфазной машиной, для которой можно нарисовать известные четыре схемы замещения. Например, для обмотки управления они имеют следующий вид (рис. 1.3)

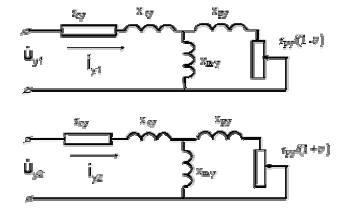
Рис. 1.3. Схемы замещения обмотки управления

Здесь: 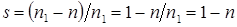; 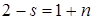, где 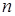– относительная частота вращения.

Эти схемы позволяют получить уравнения токов, по которым можно вывести уравнения механических, регулировочных и прочих характеристик. Однако, полученные уравнения будут слишком громоздкими. Для асинхронного исполнительного двигателя ситуацию можно существенно упростить, если в схемах замещения пренебречь всеми сопротивлениями, кроме активного сопротивления ротора 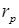. Такие схемы, да и сами двигатели, будем называть "идеальными" (рис.1.4). Основанием для идеализации служит тот факт, что исполнительные двигатели выполняются с роторами, имеющими большое активное сопротивление.

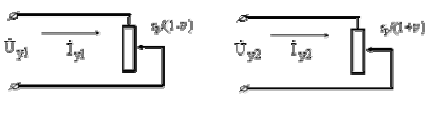
Для последних схем замещения уравнения токов принимают вид:

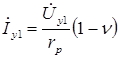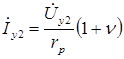; (16.1)

16.3. Характеристики асинхронного исполнительного двигателя
при разных способах управления

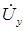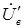, Свойства и поведение асинхронного исполнительного двигателя определяются механическими и регулировочными характеристиками.

В общем случае напряжения и образуют несимметричную систему векторов (рис.1.5).

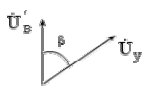
Рис. 1.5.

Используя понятие эффективного коэффициента сигнала, можно записать

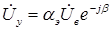
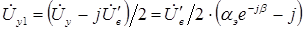
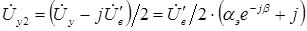
Симметричные составляющие напряжения управления будут:

Переходя от показательных функций к тригонометрическим и учитывая, что 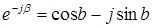, подставим полученные значения 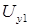и 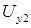в (1.1)

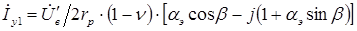
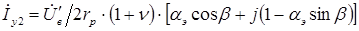(16.2)

Электромагнитная мощность с точки зрения передачи энергии со статора на ротор представляет собой сумму электромагнитных мощностей прямой и обратной последовательностей. При круговом поле они равны потерям в роторе, деленным на скольжения /в нашем случае на 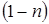и /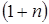

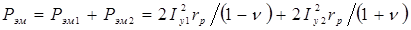
Так как по отношению к полю прямой последовательности машина работает в режиме двигателя, а по отношению к полю обратной последовательности в режиме электромагнитного тормоза, то результирующий момент М равен

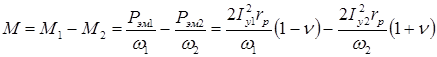
Подставим в это уравнение квадраты модулей токов 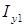и 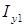из (1.2). После преобразований, получим:

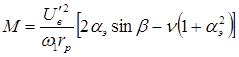
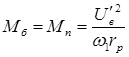
Выразим момент двигателя в относительных единицах. За базисный возьмем пусковой момент, развиваемый двигателем при круговом поле ( , , )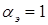

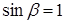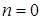Тогда момент в относительных единицах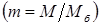

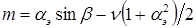(16.3)

Уравнение (1.3) есть аналитическое выражение механических характеристикидеального асинхронного исполнительного двигателя, под которыми понимают зависимость момента от угловой скорости вращения при постоянном коэффициенте сигнала.

Решив уравнение (1.3) относительно 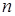, получим выражение регулировочных характеристик, которые показывают зависимость угловой скорости вращения от коэффициента сигнала при постоянном моменте на валу

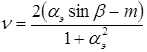(16.4)

Рассмотрим механические и регулировочные характеристики а также характеристики мощности при различных способах управления идеальным асинхронным исполнительным двигателем.