Получение кругового поля в конденсаторном микродвигателе
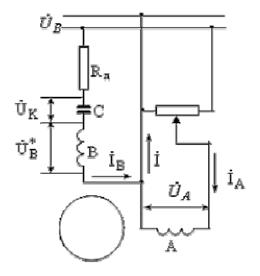
Рис.5.7. Схема включения конденсаторного двигателя (общий случай)
Рассмотрим двигатель с двумя обмотками  и
и  (рис. 5.7). Последовательно с обмоткой В кроме конденсатора С включено добавочное сопротивление
(рис. 5.7). Последовательно с обмоткой В кроме конденсатора С включено добавочное сопротивление  , а главная обмотка питается от сети через делитель напряжения.
, а главная обмотка питается от сети через делитель напряжения.
Необходимым условием получения кругового поля является равенство нулю одной из последовательностей токов, например, обратной
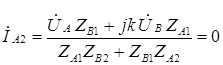 (5.4)
(5.4)
Это значит, что
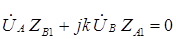 (5.5)
(5.5)
Обозначим через коэффициент 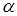 отношение напряжения на обмотке
отношение напряжения на обмотке  к напряжению сети
к напряжению сети 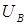 :
: 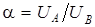 .
.
Раскрывая полные сопротивления 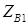 и
и 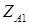 , получим
, получим
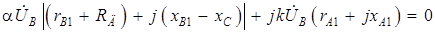 .
.
Используя (5. ), выразим параметры обмотки В через параметры обмотки А:
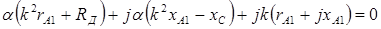 (5.6)
(5.6)
Комплексное число равно нулю, если равны нулю действительная и мнимая части:
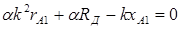 ;
; 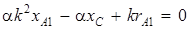 . (5.7)
. (5.7)
Таким образом, если одновременно выполнить условия (5.6) и (5.7), поле в двигателе станет круговым.
На практике круговое поле в конденсаторном двигателе получают одним из следующих способов:
1) подбором емкости конденсатора 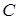 и коэффициента трансформации
и коэффициента трансформации 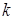 ;
;
2) подбором емкости конденсатора 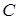 и соотношения фазных напряжений
и соотношения фазных напряжений 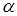 ;
;
3) подбором емкости конденсатора 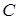 и добавочного сопротивления
и добавочного сопротивления  .
.
1. Получение кругового поля подбором емкости конденсатора и коэффициента трансформации.
При  ,
,  (рис. 5.8) уравнения (5.6), (5.7) принимают вид
(рис. 5.8) уравнения (5.6), (5.7) принимают вид
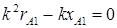 ;
; 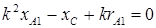 . (5.8)
. (5.8)
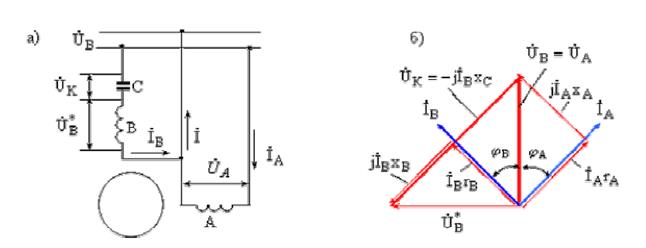
Рис. 5.8. Схема включения (а) и векторная диаграмма (б) конденсаторного
двигателя при  и
и 
Решая первое уравнение системы (5.8), найдем коэффициент трансформации
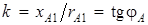
где 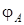 – угол между током и напряжением фазы
– угол между током и напряжением фазы 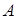 .
.
Решая второе уравнение системы (5.8), найдем емкостное сопротивление конденсатора
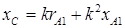 .
.
Или с учетом 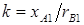 ,
, 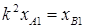
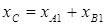
Зная 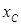 , легко определить емкость конденсатора, мкФ
, легко определить емкость конденсатора, мкФ
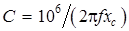 .
.
Поскольку полные сопротивления  ,
,  ,
, 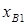 зависят от скольжения, а коэффициент трансформации и емкость конденсатора должны иметь конкретные значения, круговое поле в двигателе будет иметь место лишь при определенном скольжении
зависят от скольжения, а коэффициент трансформации и емкость конденсатора должны иметь конкретные значения, круговое поле в двигателе будет иметь место лишь при определенном скольжении 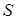 . Таким скольжением чаще всего выбирают скольжение
. Таким скольжением чаще всего выбирают скольжение 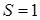 или
или 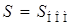 . Во всех остальных режимах, т.е. при всех остальных скольжениях, поле в микродвигателе будет эллиптическим.
. Во всех остальных режимах, т.е. при всех остальных скольжениях, поле в микродвигателе будет эллиптическим.
На рис. 5.8, б построена векторная диаграмма асинхронного конденсаторного двигателя при круговом поле, из которой можно определить рабочее напряжение конденсатора – второй, после емкости, важный параметр конденсатора
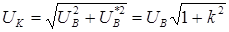 .
.
2. Получение кругового поля подбором емкости конденсатора и соотношения фазных напряжений
В этом случае (рис. 5.9) уравнения (5.6), (5.7) принимают следующий вид
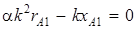 ;
; 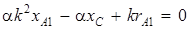 .
.
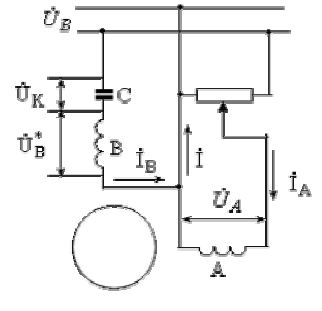
Рис.5.9. Схема включения конденсаторного двигателя при 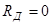 и
и 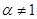
Решая систему (5.9), найдем
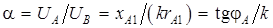 ;
;
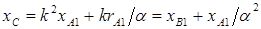 .
.
3. Получение кругового поля подбором емкости конденсатора и добавочного сопротивления
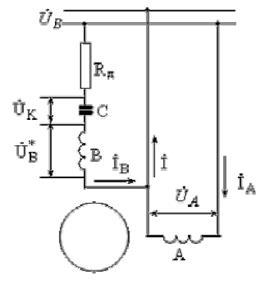
Рис.5.10. Схема включения конденсаторного двигателя при  и
и 
Схема включения показана на рис. 5.10. Уравнения (5.6), (5.7) принимают вид
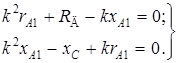 ;
;
Откуда находим:
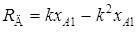 ;
;
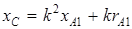 .
.
Данный способ имеет одно ограничение: разность 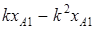 должна быть >0.
должна быть >0.
Необходимо еще раз подчеркнуть, что все три способа позволяют получить круговое поле только при одном скольжении. При всех других оно становится эллиптическим.
6. Асинхронный двигатель с пусковым
конденсатором
Двигатель пускают как однофазный, а при достижении определенной частоты вращения вспомогательную обмотку отключают и он продолжает работать как однофазный (рис. 6.1)
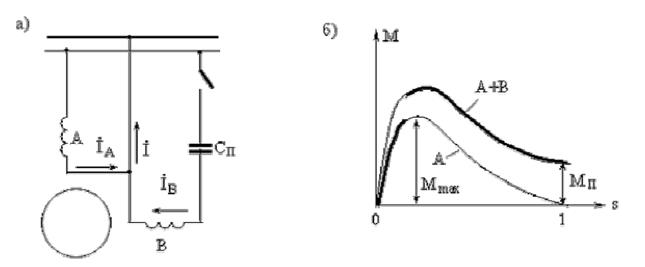
Рис. 6.1. Схема включения (а) и механическая характеристика (б) асинхронного
двигателя с пусковым конденсатором
В целях лучшего использования обмоток, главную обмотку укладывают в 2/3 пазов статора, а вспомогательную – в 1/3 пазов статора. Число витков вспомогательной обмотки, емкость конденсатора выбирают исходя из условия получения кругового поля при пуске. Правда, поскольку 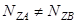 , для расчета
, для расчета 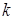 и
и 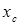 следует использовать формулы ( . ).
следует использовать формулы ( . ).
На рис. 6.2 приведена круговая диаграмма пусковых токов при изменении емкости конденсатора.
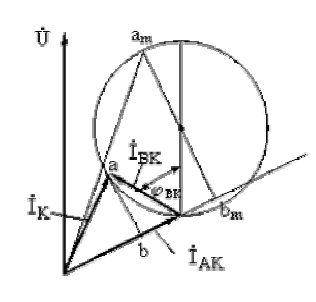
Рис.6.2. Круговая диаграмма пусковых токов асинхронного двигателя с пусковым конденсатором
Известно, что пусковой момент несимметричного двухфазного асинхронного двигателя пропорционален произведению амплитуд МДС фаз 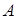 ,
, 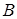 и синусам углов их пространственного
и синусам углов их пространственного 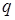 и временного
и временного 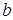 сдвигов (1.10). Поскольку
сдвигов (1.10). Поскольку 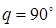 ,
, 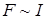 , параметры фазы
, параметры фазы 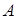 постоянны, получается, что
постоянны, получается, что
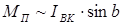 .
.
Согласно рис. 6.1, 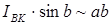 . Таким образом,
. Таким образом,
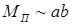 . (6.1)
. (6.1)
Из круговой диаграммы можно найти наибольший пусковой момент двигателя, который определяется отрезком 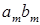 , полученным как перпендикуляр, проведенный через центр окружности к продолжению вектора тока
, полученным как перпендикуляр, проведенный через центр окружности к продолжению вектора тока 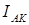
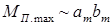 ,
,
после чего нетрудно определить емкость конденсатора, обеспечивающего этот момент.
Двигатель имеет неплохие пусковые параметры 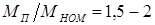 ;
; 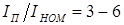 , но низкие энергетические показатели в номинальном режиме:
, но низкие энергетические показатели в номинальном режиме: 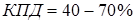 ,
, 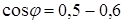 ;
; 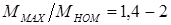 .
.
Дата добавления: 2022-02-05; просмотров: 534;











