Система счисления в остаточных классах (СОК)

Поиски новых путей повышения эффективности выполнения арифметических операций привели к заключению, что в рамках обычной позиционной системы счисления ускорения операций добиться сложно. Следует отметить, что позиционные системы счисления обладают существенным недостатком – наличием межразрядных связей, влияющих на способы реализации арифметических операций. В конечном итоге это приводит к усложнению аппаратуры и снижению быстродействия. Оказалось, что арифметика, в которой межразрядные связи отсутствовали бы, может быть построена на основе непозиционной системы счисления, в частности системы счисления в остаточных классах. В системе остаточных классов числа представляются остатками от деления на выбранную систему оснований и все рациональные операции могут выполняться параллельно над цифрами каждого разряда в отдельности. В то же время системе остаточных классов присущи некоторые недостатки: ограниченность действий этой системы полем целых положительных чисел, трудность определения соотношений чисел по величине, определения выхода результата операции из диапазона и некоторые другие.

Определение. Если задан ряд положительных целых чисел p₁, p₂, ..., p_n, называемых в дальнейшем основаниями системы, то под системой счисления в остаточных классах будем понимать такую систему, в которой целое положительное число представляется в виде набора остатков ( вычетов ) по выбранным основаниям

N = (a₁, a₂, ..., a_n),

причем образование цифр a_i осуществляется следующим образом:

a_i = N - 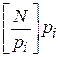, для i = 1, 2, ..., n, (5)

где [] означает целую часть, то есть цифра i-го разряда a_i числа N есть наименьший положительный остаток от деления N на p_i.

Таким образом, в СОK в отличие от обобщенной позиционной системы счисления образование цифры каждого разряда производится независимо друг от друга. Очевидно, что a_i < p_i.

В теории чисел доказано, что если числа p_i взаимно простые между собой, то описанное цифрами a₁, a₂, ..., a_n представление числа N -- единственно.

Диапазон представимых чисел в СОK равен:

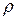= p₁, p₂, ..., p_n.

Рассмотрим правила выполнения операций сложения и умножения в СОK в случае, если числа и результат находятся в диапазоне [O, ].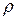

Пусть операнды A и B представлены соответственно остатками a_i и b_i по основаниям p_i, i=1,2, ... ,n. Результаты операций A+B и A∙B представлены остатками g_i и d_i по тем же основаниям p_i, то есть

A=(a₁ a₂ ... ,a_n),

B=(b₁, b₂, ... ,b_n),

A+B=(g₁, g₂, ... ,g_n),

A∙B=(d₁, d₂, ... ,d_n),

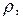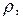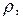при этом A < B < A+B < A∙B <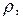

g_i º a_i + b_i (mod p_i),

то есть g_i сравнимо с a_i + b_i по модулю p_i;

d_i º a_i b_i (mod p_i).

При этом

g_i º a_i + b_i - ,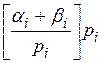

d_i º a_i b_i - .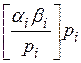

С учетом (5) отсюда следует:

g_i = A+B - 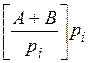. (6)

Из представления A и B следует:

А = k_i p_i + a_i,

B = l_i p_i + b_i,

где k_i и l_i - целые неотрицательные числа.

Тогда A + B = (k_i + l_i) p_i + a_i + b_{i ,}

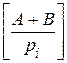=k_i + l_i + ,

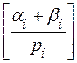A + B = (k_i + l_i)p_i + .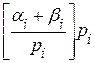

Подставляя полученные выражения в (6), получим:

g_i º a_i + b_i - 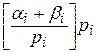. (7)

В случае умножения

d_i º a_i b_i - .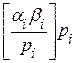

Аналогично сложению (A + B) получим:

A∙B = k_i l_i p_i² + (a_i l_i +b_i k_i)p_i + a_i b_i,

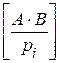= k_i l_i p_i + a_i l_i +b_i k_i + .

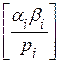Таким образом,

d_i º a_i b_i - 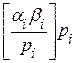. (8)

Пример. Сложить числа А = 23 и В = 48 в СОК.

Пусть основаниями системы являются p₁ = 3, p₂ = 5, p₃ = 7.

По выбранным основаниям числа А и В в СОК примут вид:

А = 23 = (2, 3, 2),

B = 48 = (0, 3, 6),

получим А + В = (2, 1, 1).

Легко проверить, что 23 + 48 = 71, а число 71 = (2, 1, 1) в СОК.

Пример. Умножить число А=14 на В=8 в СОК.

А=14=(2, 4, 0),

B=8=(2, 3, 1).

В соответствии с (4) получим:

g₁ = 4 - 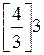= 4 - 3 = 1,

g₂ = 12 - 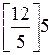= 12 - 2∙5 = 2,

g₃ = 1 - 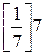= 1 - 0.7 = 1.

Таким образом, А∙В = 122 = (1, 2, 1).

Охарактеризуем в общих чертах достоинства и недостатки введенной СОK.

Достоинства:

§ независимость образования разрядов числа, в силу чего каждый разряд несет информацию обо всем исходном числе, а не о промежуточном числе, получившемся в результате формирования младших разрядов (позиционная система счисления). Отсюда вытекает независимость разрядов числа друг от друга и возможность их параллельной обработки, что в свою очередь в дальнейшем позволяет вводить принципиально новые методы арифметического контроля. При введении дополнительного контрольного основания остаток, взятый по этому основанию, при его избыточности позволяет контролировать и исправлять ошибки в цифрах по рабочим основаниям;

§ малоразрядность остатков, представляющих число. Ввиду малого количества кодовых комбинаций открывается возможность построения табличной (не вычислительной) арифметики.

Недостатки:

§ невозможность визуального сопоставления чисел, так как внешняя запись числа не дает представления о его величине;

§ отсутствие простых признаков выхода результата операций за пределы [0,ρ];

§ ограниченность действий системы сферой целых положительных чисел;

§ получение во всех случаях точного результата исключает возможность приближенных вычислений, округлений.