Двоично-десятичные коды

Пусть число A представлено в системе счисления с основанием r:

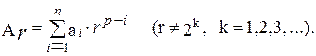
Цифры a_i будем представлять двоичными разрядами d₁,d₂,…,d_m. Каждому двоичному разряду припишем веса p₁,p₂,…,p_m. Тогда каждый разряд a_i числа A будет иметь вид 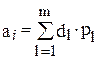, а все число

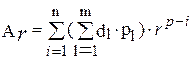, (4)

где n и m определяют общее число двоичных разрядов.

Если каждый разряд числа имеет вес и при r≠2^k не выполняется равенство p_k=r ∙ p_k-1, то системы принято называть взвешенными. Количество разрядов m должно удовлетворять выражению m ≥ log₂r. Если десятичное число записано в виде (4), то будем говорить, что число представлено в двоично-десятичном коде. Наибольшее распространение из них получили коды, в которых десятичная цифра представляется двоичной тетрадой (BCD-коды). Существует множество способов кодирования десятичных цифр. Существенным при этом является простота представления инверсных кодов и простота выделения (формирования) сигнала переноса из цифры в цифру.

Сформулируем набор требований, позволяющих упростить выполнение арифметических операций и операций перевода чисел.

§ Четность, состоит в том, что четным десятичным цифрам соответствуют только четные двоичные коды и наоборот. Это обеспечивает эффективность операций округления, умножения и деления чисел в BCD-кодах.

§ Дополняемость, заключается в том, что сумма двоичного кода и инверсного ему кода любой десятичной цифры должна быть равна 9. Это обеспечивает эффективность операции алгебраического сложения в BCD-кодах.

§ Упорядоченность, то есть большей десятичной цифре соответствует большая тетрада и наоборот.

§ Единственность представления десятичной цифры двоичной тетрадой.

§ Взвешенность, то есть каждому разряду двоичного представления десятичной цифры поставлен в соответствие вес. Это обеспечивает эффективность всех арифметических и логических операций в BCD-кодах.

Если каждая десятичная цифра кодируется соответствующим двоичным эквивалентом, то такое кодирование называется кодом прямого замещения.

BCD-код – код, взаимодополняемый до 15. Это создает некоторые неудобства при суммировании чисел - ввод поправки в некоторых случаях. В то же время этот код имеет одно существенное достоинство – аддитивность: сумма кодов равна коду суммы.

0011 код 3

0101 код 5

1000 код 8

Основной недостаток этого кода заключается в том, что инверсия какой- либо цифры оказывается цифрой, дополняющей данную цифру до 15, а не до 9.

a = 0100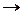

a = 1011 11, то а + а = 1111 = 15

В табл. 4 показаны различные способы кодирования десятичных цифр.

Таблица 4