ЛЕКЦИЯ 17. ОБЗОРНАЯ

Остановимся на некоторых важных нерешенных математических проблемах. Мы, разумеется, не призываем немедленно бросится на их решение. Эти проблемы, на самом деле, очень сложные и многие сильнейшие математики современности ищут их решение.

1. Гипотеза Римана.

Как известно, не существует простой закономерности, описывающей распределение простых чисел среди натуральных. Риман обнаружил, что число π(x) простых чисел, не превосходящих x, выражается через распределение нетривиальных нулей дзета-функции Римана ζ(s). Риман высказал гипотезу, не доказанную и не опровергнутую до сих пор, что все нетривиальные нули дзета-функции лежат на прямой линии ( ).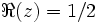

Обобщённая гипотеза Римана состоит из того же самого утверждения для обобщений дзета-функций, называемых L-функциями Дирихле.

Большинство математиков верят, что гипотеза верна. На сегодняшний день проверены первые 1 500 000 000 решений.

Гипотеза Римана входит в число семи главных нерешённых математических проблем. За её доказательство Институт математики Клея (Кембридж, Штат Массачусетс) выплатит приз в 1 млн. долларов. К рассмотрению принимаются решения, которые были опубликованы в известном математическом журнале, причём не ранее, чем через 2 года после публикации (для всестороннего рассмотрения математическим сообществом). http://www.claymath.org/millennium/

Группа математиков Университета Пардье (Purdue University, USA) под руководством Луи де Бранж де Бурсиа (Louis De Branges de Bourcia) предложила доказательство гипотезы Римана, которое на сегодняшний день не опровергнуто: http://news.uns.purdue.edu/UNS/html4ever/2004/040608.DeBranges.Riemann.html

Дзета-функция Римана ζ(s) определена с помощью ряда Дирихле:

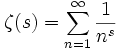
В области 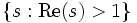, этот ряд сходится, является аналитической функцией и допускает аналитическое продолжение на всю комплексную плоскость без единицы. В этой области также верно представление в виде бесконечного произведения (тождество Эйлера)

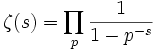
где произведение берётся по всем простым числам p. Это равенство представляет собой одно из основных свойств дзета-функции.

2. Гипотеза Кука.

Допустим, что вы, находясь в большой компании, хотите убедиться, что там же находится ваш знакомый. Если вам скажут, что он сидит в углу, то достаточно будет доли секунды, чтобы, бросив взгляд, убедиться в истинности информации. В отсутствие этой информации вы будете вынуждены обойти всю комнату, рассматривая гостей. Это говорит о том, что решение какой-либо задачи часто занимает больше времени, чем проверка правильности решения.

Стивен Кук сформулировал проблему: может ли проверка правильности решения задачи быть более длительной, чем само получение решения, независимо от алгоритма проверки. Эта проблема также является одной из нерешенных задач из области логики и информатики. Ее решение могло бы революционным образом изменить основы криптографии, используемой при передаче и хранении данных.

3. Гипотеза Ходжа.

В ХХ веке математики открыли мощный метод исследования формы сложных объектов. Основная идея заключается в том, чтобы использовать вместо самого объекта простые "кирпичики", которые склеиваются между собой и образуют его подобие. Гипотеза Ходжа связана с некоторыми предположениями относительно свойств таких "кирпичиков" и объектов.