ЛЕКЦИЯ 15. ОПИСАНИЕ ЗАДАЧ НА ЯЗЫКЕ ЛОГИКИ

Рассмотрим описание задач на языке логики. Такое описание потребует формализовать некоторые наиболее часто встречаемые условия.

Прежде всего, таким условием является

x₁ + x₂+ … +x_n =1, (15.1)

x_iÎ{0,1}.

Это условие эквивалентно следующей системе логических формул:

x₁ v x₂ v … v x_n,

Øx₁ v Øx₂,

Øx₁ v Øx₃,

…

Øx₁ v Øx_n,

…

Øx₂ v Øx_n,

…

Øx_n-1 v Øx_n.

Количество всех дизъюнктов равно 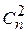+1. Число дизъюнктов можно уменьшить, если использовать дополнительные переменные и провести следующие преобразования.

Обозначим через F следующую систему формул:

x₁ + x₂ + y₁ =1,

x₃ + x₄ + y₂ =1,

F ≡ …

x_n-1 + x_n + y_n/2 =1.

Замечание. Если n – нечетное, то последняя формула заменяется на x_n + y_(n+1)/2 =1.

В F y_i - дополнительные переменные.

Теперь система (15.1) оказывается эквивалентной системе

G ≡

В свою очередь формулу Øy₁ + Øy₂ + … + Øy_n/2 = 1 можно заменить эквивалентной системой H:

J= 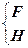. (15.2)

Описанные преобразования по аналогии применяем к системе (15.2) и т. д. до тех пор, пока не останутся только трехлитерные или двухлитерные уравнения вида a+b+c=1 или d+e=1. Каждое трехлитерное уравнение дает 4 дизъюнкта: a v b v c, Øa v Øb, Øa v Øc, Øb v Øc. Каждое двухлитерное уравнение с+d=1 дает 2 дизъюнкта: c v d, Øc v Ød. Следовательно, рассматриваемый способ построения эквивалентной системы дизъюнктов для (15.1) дает не выше 4(n-1) дизъюнктов (уточнение этой формулы требует принять во внимание четность/нечетность n). Приведем пример.

x₁ + x₂+ … +x₁₀ =1,

x_iÎ{0,1}.

Последовательно получаем эквивалентные системы:

x₁ + x₂ + y₁ =1,

x₃ + x₄ + y₂ =1,

x₅ + x₆ + y₃ =1, (15.3)

x₇ + x₈ + y₄ =1,

x₉ + x₁₀ + y₅ =1,

Øy₁ + Øy₂ + Øy₃ + Øy₄ + Øy₅ =1

и

x₁ + x₂ + y₁ =1,

x₃ + x₄ + y₂ =1,

x₅ + x₆ + y₃ =1, (15.4)

x₇ + x₈ + y₄ =1,

x₉ + x₁₀ + y₅ =1,

Øy₁ + Øy₂ + z₁ =1,

Øy₂ + Øy₃ + z₂ =1,

Øy₅ + z₃ =1,

Øz₁ + Øz₂ + Øz₃ =1.

Теперь все уравнения (кроме одного) трехчленные. Каждое из них дает 4 дизъюнкта. Всего дизъюнктов 34, вместо 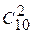+1 = 46.

Рассмотрим другие важные условия.

x₁ + x₂+ … +x_n £ 1, (15.5)

x_iÎ{0,1}.

Это условие трансформируется в эквивалентную систему двухлитерных дизъюнктов

Øx₁ v Øx₂,

Øx₁ v Øx₃,

…

Øx₁ v Øx_n,

…

Øx₂ v Øx_n,

…

Øx_n-1 v Øx_n.

На практике важно условие вида

x₁ + x₂+ … +x_n = k , (15.6)

x_iÎ{0,1}, k > 1, k £ n, k - целое.

Прямое кодирование этого равенства при k=n/2 (n - четное) требует экспоненциально растущего от n числа дизъюнктов. Поэтому следует вводить новые переменные. В целях ясности обратимся к иллюстративному примеру.

x₁ + x₂+ … +x₈ =3. (15.7)

Равенство (15.7) можно заменить следующей эквивалентной системой равенств

x₁ + y₄+ y₅+ y₆+ y₇+y₈ =1,

x₂ + z₄+ z₅+ z₆+ z₇+z₈ =1,

x₃ + w₄+ w₅+ w₆+ w₇+w₈ =1,

y₄+ z₄+ w₄ £ 1,

y₅+ z₅+ w₅ £ 1,

…

y₈+ z₈+ w₈ £ 1,

x₄ º y₄ v z₄ v w₄,

x₅ º y₅ v z₅ v w₅,

_{. . .}

x₈ º y₈ v z₈ v w₈.

При этом для k первых переменных из (15.8) записываем k равенств вида

x₁ + y_k+1 + y_k+2 + y_k+3 + …+ y_n = 1,

x₂ + z_k+1 + z_k+2 + z_k+3 + …+ y_n = 1,

. . . (15.9)

x_k + w_k+1 + w_k+2 + w_k+3 + …+ w_n = 1.

Пусть x₁ = x₂=…= x_k = 0. Тогда, например, y_a = z_b … = w_c = 1, причем a ¹ b, a ¹ c, …, b ¹ c. Следовательно, в силу наших условий, некоторые k переменных из числа x_k+1, x_k+2,…, x_n будут иметь единичные значения, обеспечивая условие (15.9). Если, например, x₁ = 1, x₂ =…= x_k = 0, то некоторые (k - 1) переменных (и только они) из числа переменных x_k+1, x_k+2,…, x_n будут иметь единичные значения и т.п. Число дизъюнктов для (15.9) составит порядка 4k×(n - 1). Общее число дизъюнктов для (15.9) составит порядка 4k×(n - 1)+ 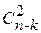(эквивалентности

x_k+1 º y_k+1 v z_k+1 v… v w_k+1,

x_k+2 º y_k+2 v z_k+2 v … v w_k+2,

…

x_n º y_n v z_n v … v w_n

в систему дизъюнктов преобразованной задачи нет необходимости включать).

Пример 1.1. В хищении подозреваются A,B и C.

1. Никто, кроме A,B,C в хищении не замешан.

2. A никогда не ходит на дело без соучастников.

3. С не виновен, если виновен B.

Спрашивается, виновен ли A?

Нужно составить систему логических уравнений, введя необходимые булевские переменные. Обозначим: x_a – виновен A, x_b – виновен B, x_c – виновен C. Составим следующую базу знаний:

1. x_a v x_b v x_c ,

2. x_a ® x_b v x_c ,

3. x_b ® Øx_c .

Эти логические формулы соответствуют условиям задачи. Можно воспользоваться арифметическим представлением логических формул. Этот прием даст связь между логическими формулами и рассмотренными выше условиями формализации. Арифметические представления таковы:

f v g v … v h º f + g+ … + h ³ 1,

Øf º (1- f), (15.10)

f ® g º Ø f v g º (1- f) + g ³ 1,

f & g º f + g = 2 º Øf + Øg = 0 º f×g.

Теперь условия нашей задачи получат следующее представление:

1. x_a + x_b + x_c ³ 1,

2. (1-x_a ) + x_b + x_c ³ 1.

3. (1-x_a ) + (1- x_c ) ³ 1.

Относительно этой модели знаний поставлен вопрос: верно ли, что x_a = 1?

Рассмотрим описание задач на языке логики. Такое описание потребует формализовать некоторые наиболее часто встречаемые условия.

Прежде всего, таким условием является

x₁ + x₂+ … +x_n =1, (15.11)

x_iÎ{0,1}.

Это условие эквивалентно следующей системе логических формул:

x₁ v x₂ v … v x_n,

Øx₁ v Øx₂,

Øx₁ v Øx₃,

…

Øx₁ v Øx_n,

…

Øx₂ v Øx_n,

…

Øx_n-1 v Øx_n.

Количество всех дизъюнктов равно 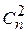+1.

Рассмотрим другие важные условия.

x₁ + x₂+ … +x_n £ 1, (15.12)

x_iÎ{0,1}.

Это условие трансформируется в эквивалентную систему двухлитерных дизъюнктов

Øx₁ v Øx₂,

Øx₁ v Øx₃,

…

Øx₁ v Øx_n,

…

Øx₂ v Øx_n,

…

Øx_n-1 v Øx_n.