Лекция 1 Вычисление определенных интегралов численными методами

План лекции:

1. Вычисление определенных интегралов методом левых, правых и средних прямоугольников.

2. Вычисление определенных интегралов методом трапеций.

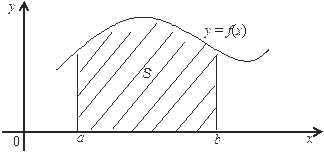
Определенный интеграл от непрерывной функции f(х) ³ 0 в пределах от а до b представляет площадь криволинейной трапеции S, ограниченной кривой f(x), осью абсцисс и прямыми х = а, х = b (рисунок 1). Из курса высшей математики известно, что

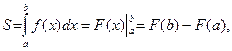
где F(x) – первообразная для f(х) на отрезке [а, b], т. е. F¢(x) = f (х)на отрезке [a, b]. Если f(х) < 0 на отрезке [a, b], то в формуле S < 0, но çSçравно площади криволинейной трапеции, находящейся под осью абсцисс.

S

Рисунок 1 – Определенный интеграл – площадь криволинейной трапеции

Однако на практике приведенной формулой часто нельзя воспользоваться по двум основным причинам: 1) вид функции f(x) не допускает непосредственного интегрирования, т. е. первообразную нельзя выразить в элементарных функциях; 2) значения функции f(x) заданы только на фиксированном конечном множестве точек x_i, т. е. функция задана в виде таблицы. В этих случаях используются методы численного интегрирования. Они основаны на аппроксимации подынтегральной функции некоторыми более простыми выражениями, например многочленами нулевой (у = с), первой (у = сх + d) или второй (у = сx² + dх + k) степени, а численные методы вычисления определенного интеграла, основанные на подобной аппроксимации, называются соответственно методами прямоугольников, трапеций и Симпсона (парабол).

Пусть требуется приближенно вычислить значение интеграла 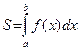.В методе прямоугольников криволинейная трапеция разбивается на п частей, каждая из которых представляет собой прямоугольник, основание которого равно шагу интегрирования 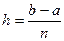, а длины сторон соответственно Y₀ = f(x₀), Y₁ = f(x₁), Y_n = f(x_n), где x₀ = a, x₁, …, x_n-1, x_n = b – точки деления отрезка [a, b] на n равных частей.

Различают методы правых, левых и средних прямоугольников, в зависимости от месторасположения начальной точки x₀ при вычислении площади элементарного прямоугольника. Если за высоту каждого прямоугольника принимается левая ордината (y₀, y₁, y₂…), то вычисление интеграла будет производиться по методу левых прямоугольников; если правая ордината (y₁, y₂, y₃…), то по методу правых прямоугольников; если за высоту принимается середина интервала длиной h, то будет применяться метод средних прямоугольников. Основанием всех прямоугольников будет являться величина шага интегрирования h.

Тогда при методе левых прямоугольников:

,

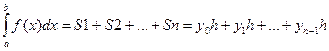при методе правых:

,

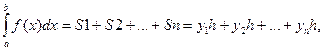при методе средних:

.

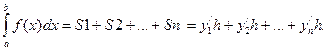Таким образом, первоначальное значение 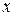при методе левых прямоугольников 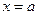, правых – 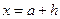, средних – 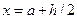. Последующие значения 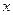будут получаться через операцию присваивание 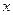= 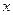+ h, а элементарные площади S1, S2…Sn будут вычисляться по формуле 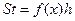. Сумма этих площадей дает значение интеграла. Изложенное выше реализует алгоритм (рисунок 2), где 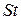- значения элементарных площадей, а их сумма S – значение интеграла.

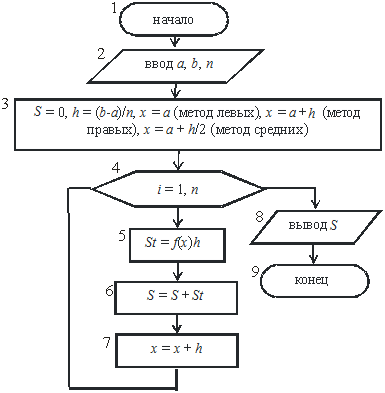
Рисунок 2 – Схема алгоритма вычисления интеграла методом прямоугольников

Более точное значение интеграла получается при вычислении его методом трапеций, когда ординаты (y₀, y₁, y₂… y_n) подынтегральной функции соединяют отрезками прямых и искомую площадь заменяют суммой площадей трапеций, высотой которых является шаг h, а основаниям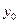и и 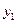для S1, 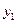и 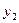для S2 (рисунок 3).

Тогда

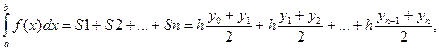
где 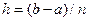, а y₀, y₁, y₂ … y_n равны значениям функции 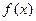при соответствующих значениях аргумента .

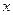Поскольку 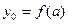, , 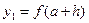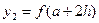и т. д., то схема алгоритма примет вид, приведенный на рисунке 3. В приведенном алгоритме блок 5 вычисляет значение элементарных площадей S1, S2,…Sn, в блоке 6 осуществляется их суммирование и блоком 7 изменяется 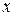на величину шага h.

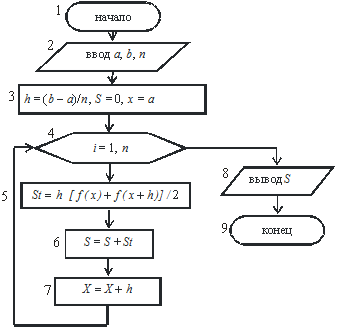
Рисунок 3 – Схема алгоритма вычисления интеграла методом трапеций