Лекция 4. Область определения и область значений функции. Способы задания функции. Свойства функции. Основные элементарные функции, их свойства и графики.
Основные определения.
Опр. Функцией называется закон, по которому каждому значению независимой переменной 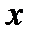 , называемой аргументом, ставится в соответствие единственное значение зависимой переменной
, называемой аргументом, ставится в соответствие единственное значение зависимой переменной 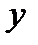 , называемой функцией:
, называемой функцией: 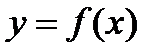 , где
, где 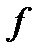 – закон соответствия.
– закон соответствия.
Пример 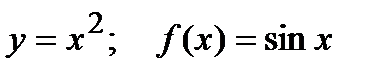 .
.
Опр. Областью определения функции (ООФ: 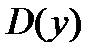 ) называется множество допустимых действительных значений аргумента, при которых функция имеет смысл в области вещественных чисел; множество значений, которые при этом принимает функция, называется ее областью значений (
) называется множество допустимых действительных значений аргумента, при которых функция имеет смысл в области вещественных чисел; множество значений, которые при этом принимает функция, называется ее областью значений ( 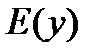 ) .
) .
Опр. Геометрическое место точек, абсциссы которых равны значению аргумента, а ординаты – значению функции, называется графиком функции.
Опр. Если выполняется равенство 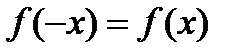 , то функция называется четной, а при выполнении равенства
, то функция называется четной, а при выполнении равенства 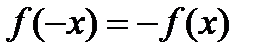 – нечетной.
– нечетной.
Опр. Если функция не является ни четной, ни нечетной, то она называется функцией общего вида.
Пример 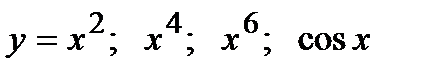 – четные функции;
– четные функции;
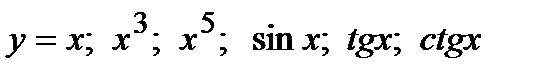 – нечетные функции;
– нечетные функции;
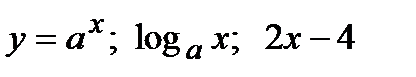 – функции общего вида.
– функции общего вида.
Опр. Функция называется периодической, если существует такое вещественное число 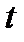 , что
, что 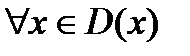 выполняется равенство
выполняется равенство 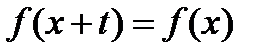 , при этом меньшее положительное число
, при этом меньшее положительное число 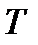 , при котором выполняется указанное равенство, называется периодом функции.
, при котором выполняется указанное равенство, называется периодом функции.
Пример 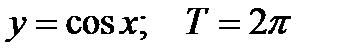 , так как
, так как 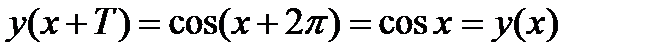 .
.
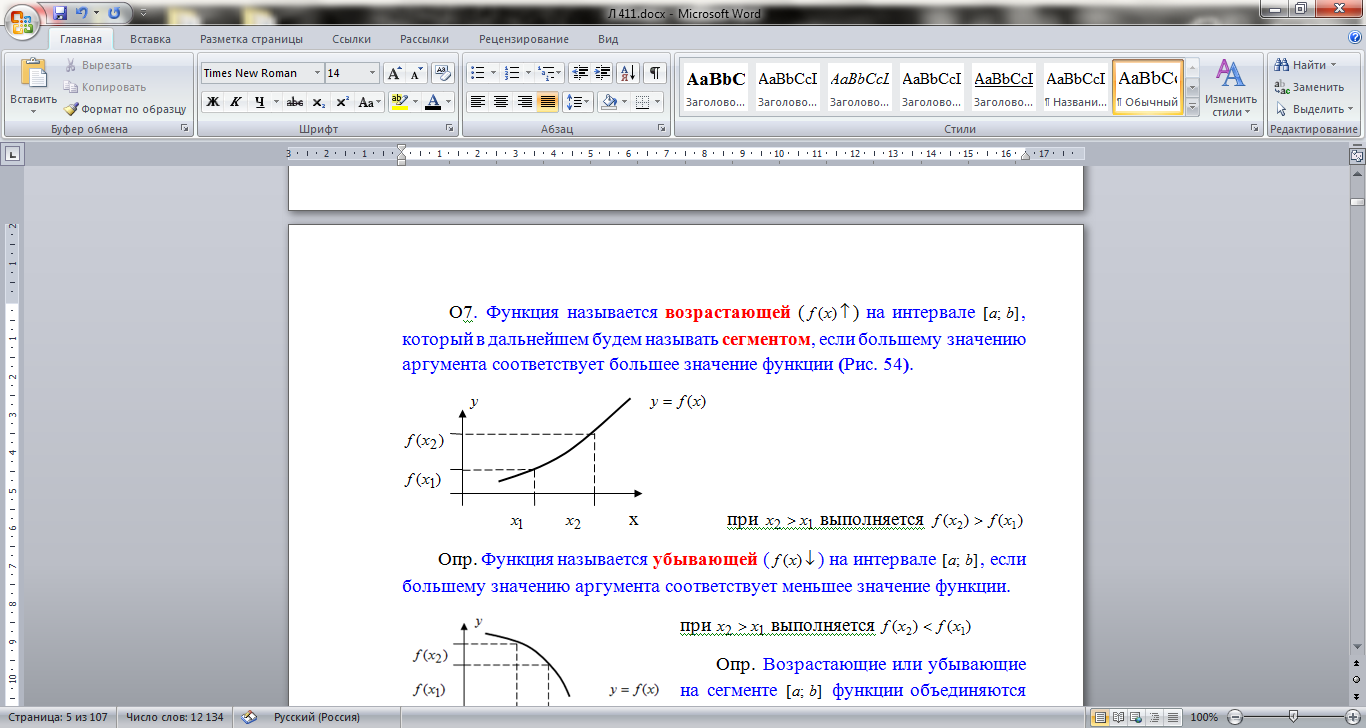 Опр. Функция называется возрастающей (
Опр. Функция называется возрастающей ( 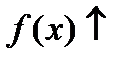 ) на интервале
) на интервале 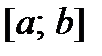 , который в дальнейшем будем называть сегментом, если большему значению аргумента соответствует большее значение функции.
, который в дальнейшем будем называть сегментом, если большему значению аргумента соответствует большее значение функции.
при 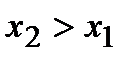 выполняется
выполняется 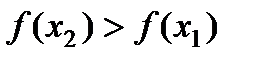
Опр. Функция называется убывающей ( 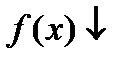 ) на интервале
) на интервале 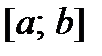 , если большему значению аргумента соответствует меньшее значение функции.
, если большему значению аргумента соответствует меньшее значение функции.
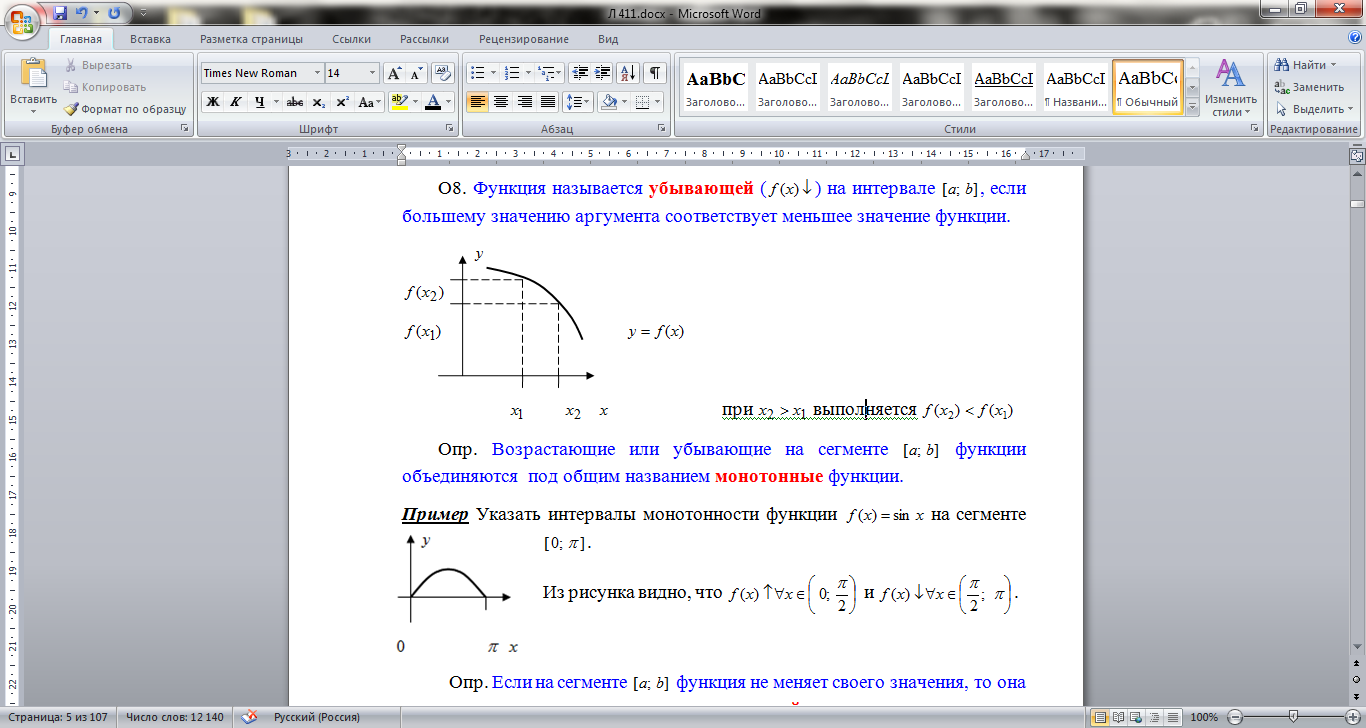 при
при 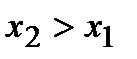 выполняется
выполняется 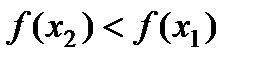
Опр. Возрастающие или убывающие на сегменте 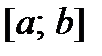 функции объединяются под общим названием монотонные функции.
функции объединяются под общим названием монотонные функции.
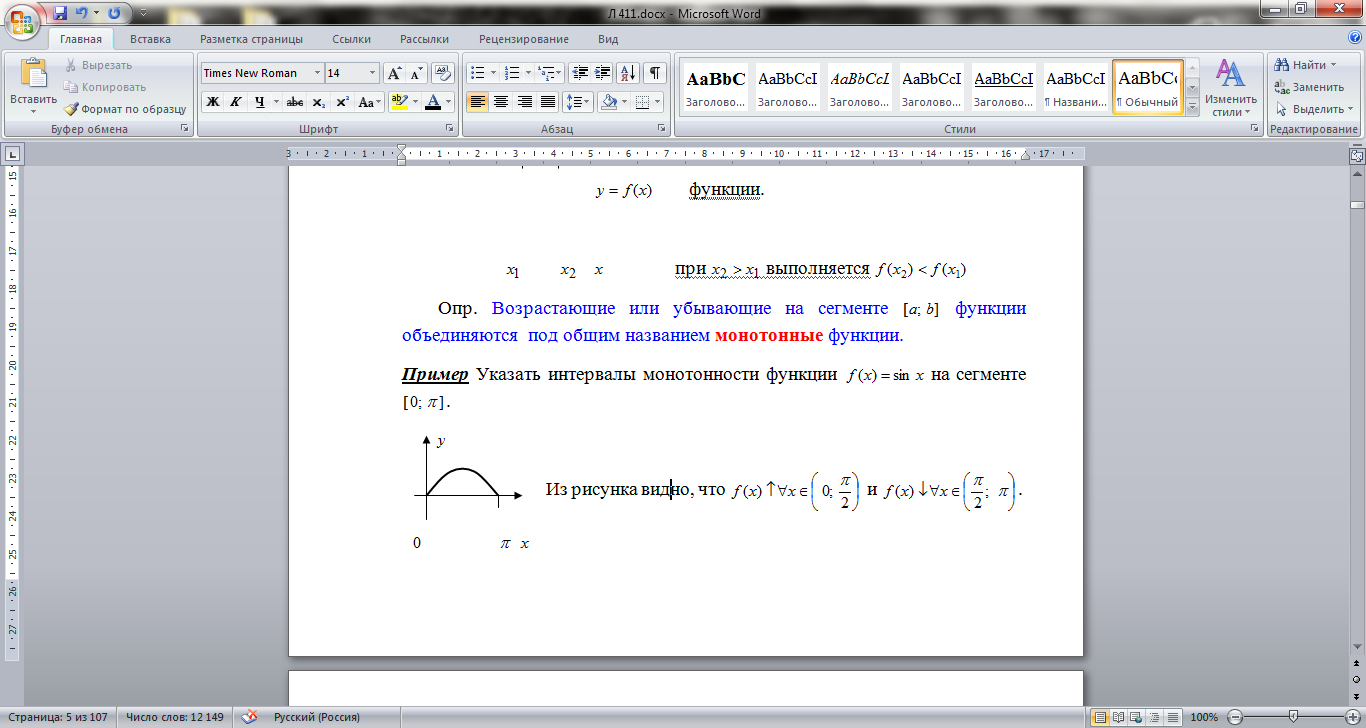 Пример Указать интервалы монотонности функции
Пример Указать интервалы монотонности функции 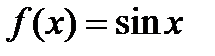 на сегменте
на сегменте 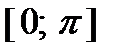 .
.
Из рисунка видно, что 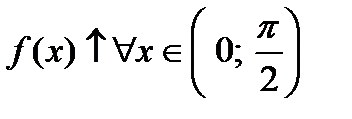 и
и 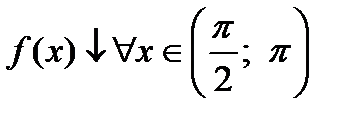 .
.
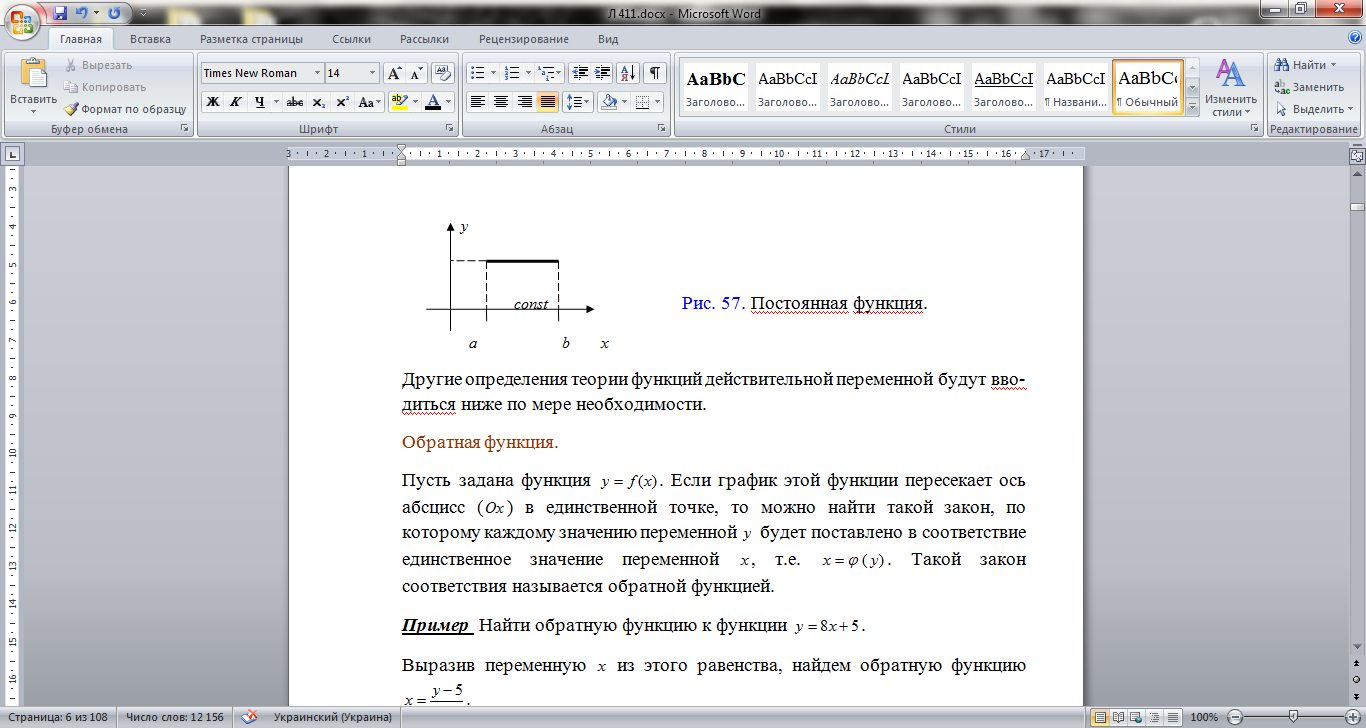 Опр. Если на сегменте
Опр. Если на сегменте 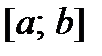 функция не меняет своего значения, то она называется постоянной.
функция не меняет своего значения, то она называется постоянной.
Другие определения теории функций действительной переменной будут вводиться ниже по мере необходимости.
Обратная функция.
Пусть задана функция 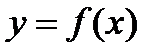 . Если график этой функции пересекает ось абсцисс (
. Если график этой функции пересекает ось абсцисс ( 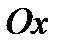 ) в единственной точке, то можно найти такой закон, по которому каждому значению переменной
) в единственной точке, то можно найти такой закон, по которому каждому значению переменной 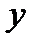 будет поставлено в соответствие единственное значение переменной
будет поставлено в соответствие единственное значение переменной 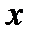 , т.е.
, т.е. 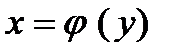 . Такой закон соответствия называется обратной функцией.
. Такой закон соответствия называется обратной функцией.
Пример Найти обратную функцию к функции 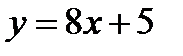 .
.
Выразив переменную 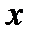 из этого равенства, найдем обратную функцию
из этого равенства, найдем обратную функцию 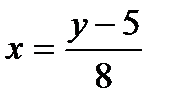 .
.
Способы задания функции.
Функция может быть задана одним из следующих способов:
– аналитический, т.е. в виде аналитической формулы (например, 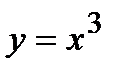 );
);
– графический, т.е. в виде графика для всех значений аргумента 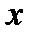 из
из 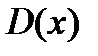 ;
;
– табличный, т.е. в виде таблицы
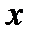
| 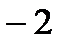
| 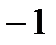
| 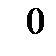
| 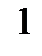
| 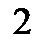
|
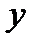
| 
| 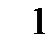
| 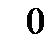
| 
| 
|
– словесный, т.е. функция задается на каждом интервале разными аналитическими формулами, графиком или таблицей, например, 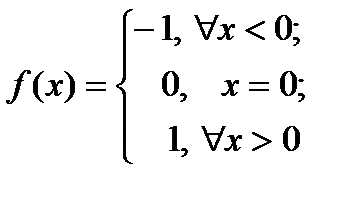 .
.
Основные элементарные функции.
Рассмотрим основные элементарные функции:
1) постоянная 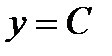 2) линейная
2) линейная 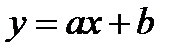
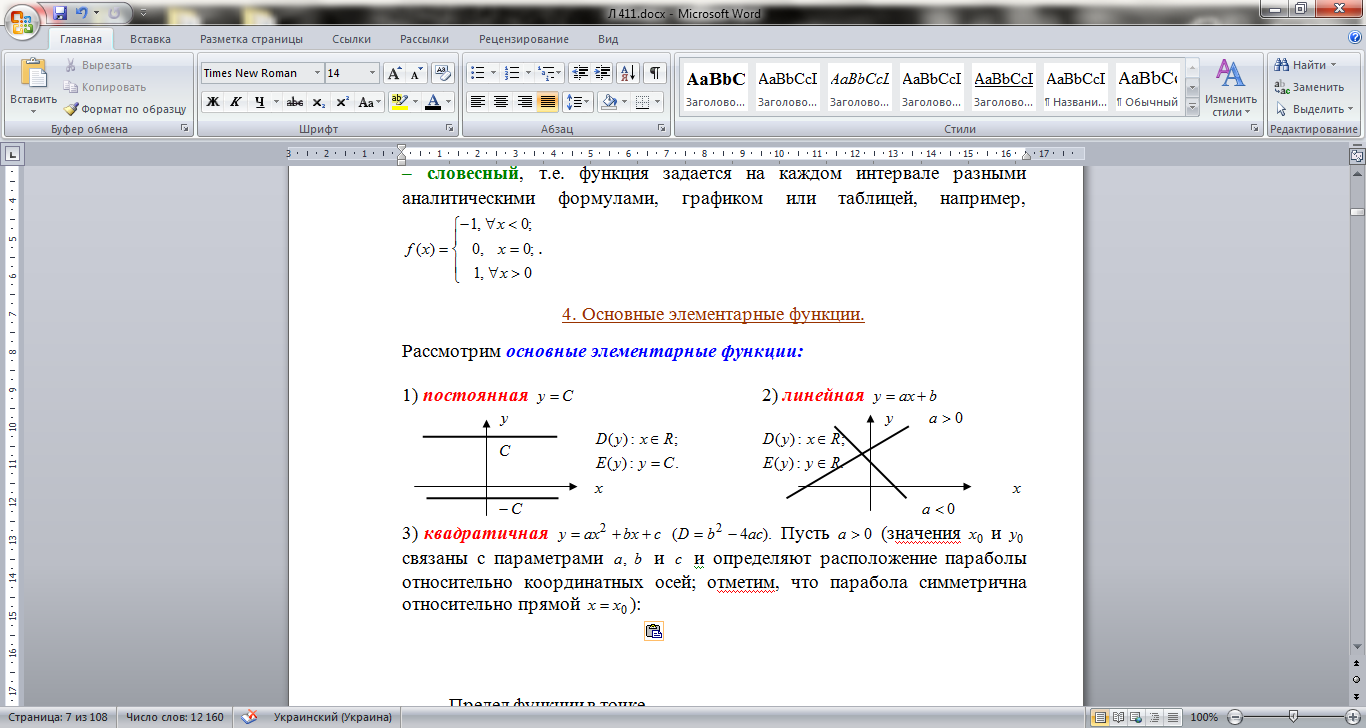
3) квадратичная 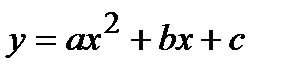
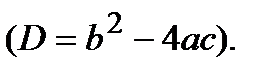 Пусть
Пусть 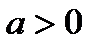 (значения
(значения 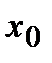 и
и 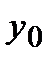 связаны с параметрами
связаны с параметрами 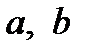 и
и  и определяют расположение параболы относительно координатных осей; отметим, что парабола симметрична относительно прямой
и определяют расположение параболы относительно координатных осей; отметим, что парабола симметрична относительно прямой 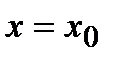 ):
):
Дата добавления: 2016-06-05; просмотров: 2953;











