Турбулентный перенос теплоты и количества движения
Турбулентное течение существенно отличается от ламинарного. На рис.5.9 показана осциллограмма колебаний скорости в определенной неподвижной точке турбулентного потока, имеющего неизменную среднюю скорость течения. Мгновенная скорость пульсирует около некоторого среднего во времени значения. Помимо показанного на графике рис.5.9 изменения абсолютной величины 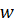 происходит еще и изменение направления мгновенной скорости. Отклонение мгновенной скорости
происходит еще и изменение направления мгновенной скорости. Отклонение мгновенной скорости 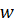 от средней во времени
от средней во времени 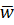 называют пульсациями скорости или пульсационными скоростями
называют пульсациями скорости или пульсационными скоростями 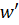 , при этом
, при этом 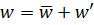 . Таким образом, турбулентное движение состоит как бы из регулярного течения, описываемого осредненными значениями скоростей, и из наложенного на него хаотического пульсационного течения.
. Таким образом, турбулентное движение состоит как бы из регулярного течения, описываемого осредненными значениями скоростей, и из наложенного на него хаотического пульсационного течения.
При пульсациях скорости происходит перенос механической энергии. Если в потоке имеет место разность температур, то пульсации скорости приводят и к переносу теплоты, вследствие чего возникают пульсации температуры (рис.5.9). Температура в определенной неподвижной точке турбулентного потока колеблется около некоторого среднего во времени значения 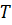 . Пульсация температуры
. Пульсация температуры 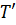 связана с
связана с 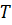 и
и 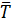 уравнением
уравнением 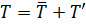 .
.
Рис.5.9. Изменение скорости 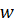 и температуры
и температуры 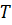
в неподвижной точке турбулентного потока
Таким образом, турбулентное течение, строго говоря, является нестационарным процессом, однако если осредненные во времени скорости и температуры 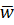 и
и 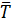 не изменяются, то такое движение и связанный с ним перенос теплоты можно рассматривать как стационарные (квазистационарные) процессы. При этом интервал времени осреднения должен быть достаточно большим по сравнению с периодом пульсации, но в то же время достаточно малым по сравнению с каким-либо характерным для осредненного движения интервалом времени, чтобы учесть возможные изменения средних скоростей и температур во времени. Будем в дальнейшем полагать, что средние значения актуальных величин
не изменяются, то такое движение и связанный с ним перенос теплоты можно рассматривать как стационарные (квазистационарные) процессы. При этом интервал времени осреднения должен быть достаточно большим по сравнению с периодом пульсации, но в то же время достаточно малым по сравнению с каким-либо характерным для осредненного движения интервалом времени, чтобы учесть возможные изменения средних скоростей и температур во времени. Будем в дальнейшем полагать, что средние значения актуальных величин 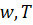 получены как среднеинтегральные.
получены как среднеинтегральные.
В общем случае пульсации скорости и температуры приводят к пульсациям давления и физических свойств.
Полагают, что выведенные в §5.2 дифференциальные уравнения конвективного теплообмена справедливы для отдельных струек пульсационного движения. Эти уравнения можно записать в осредненных значениях скорости и температуры, если произвести замену 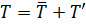 ,
, 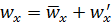 ,
, 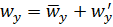 и т.д. Произведя некоторые преобразования и выдвинув дополнительные гипотезы, можно получить систему дифференциальных уравнений, описывающих в первом приближении осредненное турбулентное течение и теплообмен. В достаточно строгой постановке этот вопрос до конца не разрешен.
и т.д. Произведя некоторые преобразования и выдвинув дополнительные гипотезы, можно получить систему дифференциальных уравнений, описывающих в первом приближении осредненное турбулентное течение и теплообмен. В достаточно строгой постановке этот вопрос до конца не разрешен.
Прежде всего, рассмотрим качественную сторону явлений переноса энергии в турбулентном потоке. На основе этого рассмотрения запишем ряд соотношений, необходимых для решения простейших задач.
Пусть в некоторый момент времени 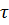 скорость в фиксированной точке (малой области) турбулентного потока имеет компоненты
скорость в фиксированной точке (малой области) турбулентного потока имеет компоненты 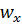 и
и 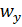 (рис.5.10). Температура жидкости в этой точке равна
(рис.5.10). Температура жидкости в этой точке равна 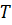 . Условную контрольную поверхность
. Условную контрольную поверхность 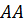 расположим близко к рассматриваемой точке и параллельно плоскости
расположим близко к рассматриваемой точке и параллельно плоскости 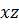 . За малый промежуток времени
. За малый промежуток времени 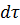 через единицу поверхности
через единицу поверхности 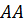 проходит масса
проходит масса 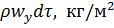 . При этом, в частности, в направлении оси
. При этом, в частности, в направлении оси 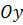 переносится количество движения относительно оси
переносится количество движения относительно оси 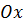 , равное
, равное 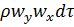 , и соответственно энтальпия
, и соответственно энтальпия 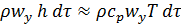 (полагаем, что
(полагаем, что 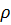 и
и 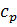 постоянны).
постоянны).
Рис.5.10. Мгновенное значение скорости в плоском турбулентном потоке
В следующие моменты времени компоненты скорости могут быть другими. Среднеинтегральное значение плотности теплового потока 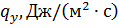 , переносимого в направлении оси
, переносимого в направлении оси 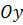 за единицу времени через единицу контрольной поверхности, будет равно:
за единицу времени через единицу контрольной поверхности, будет равно:
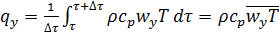 (5.31)
(5.31)
Величину 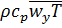 можно представить в виде
можно представить в виде
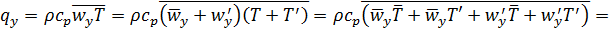
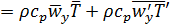 . (5.32)
. (5.32)
Здесь использованы свойства среднеинтегрального осреднения
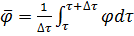 (5.33)
(5.33)
меняющихся во времени 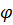 и
и 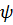 (например,
(например, 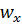 и
и 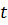 ):
):
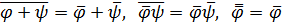 . (5.34)
. (5.34)
В дальнейшем понадобится и свойство
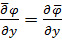 ,
,
вытекающее из (5.33) ввиду возможности изменения последовательности операций интегрирования по 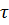 и дифференцирования по
и дифференцирования по 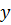 . Предполагается при этом, что интервал осреднения
. Предполагается при этом, что интервал осреднения 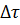 выбран согласно ранее названным условиям. Действительно, осредняя
выбран согласно ранее названным условиям. Действительно, осредняя 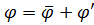 , получаем:
, получаем:
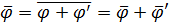 .
.
Отсюда следует, что 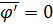 . Заметим, что
. Заметим, что 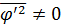 , что следует из уравнения
, что следует из уравнения 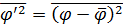 (тривиальный случай
(тривиальный случай 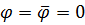 исключаем).
исключаем).
Среднеинтегральное значение количества движения относительно оси 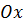 , переносимое в направлении
, переносимое в направлении 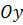 за единицу времени через единицу поверхности, можно получить аналогично получению уравнения (5.32). В результате
за единицу времени через единицу поверхности, можно получить аналогично получению уравнения (5.32). В результате
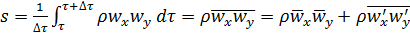 . (5.35)
. (5.35)
Аналогичные выражения в общем случае можно получить для переноса количества движения относительно любых координатных осей в направлении осей 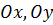 и
и 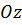 .
.
Таким образом, согласно уравнениям (5.32) и (5.35) конвективный перенос складывается из двух составляющих – осредненного и пульсационного (турбулентного) переноса. Обозначим:
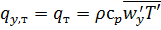 ; (5.36)
; (5.36)
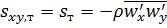 . (5.37)
. (5.37)
В общем случае 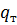 и
и 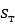 не равны нулю. Больше того, в определенных областях турбулентного потока, омывающего твердое тело,
не равны нулю. Больше того, в определенных областях турбулентного потока, омывающего твердое тело, 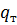 и
и 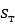 могут принимать большие значения.
могут принимать большие значения.
Рассмотрим течение около стенки, но на некотором удалении от нее. Для простоты предположим, что осредненные значения скорости и температуры изменяются только в направлении оси 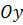 (рис.5.11). Предположим, что за счет пульсаций
(рис.5.11). Предположим, что за счет пульсаций 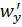 из слоя
из слоя 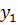 в слой
в слой 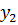 переносится энтальпия
переносится энтальпия 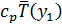 , где
, где 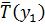 – осредненное значение температуры при
– осредненное значение температуры при 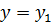 . Плоскости
. Плоскости 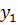 и
и 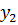 параллельны плоскости
параллельны плоскости 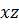 .
.
Рис.5.11. К выводу формул осредненного турбулентного
переноса теплоты и количества движения
Разность энтальпий 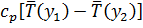 будем считать переносимой теплотой на отрезке
будем считать переносимой теплотой на отрезке 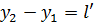 . На длине
. На длине 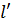 пульсация как бы не распадается, не диссипирует. Распад пульсационного движения при
пульсация как бы не распадается, не диссипирует. Распад пульсационного движения при 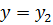 приводит к передаче энтальпии слою
приводит к передаче энтальпии слою 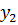 , в рассматриваемом квазистационарном течении эта передача порождает пульсацию температуры в слое
, в рассматриваемом квазистационарном течении эта передача порождает пульсацию температуры в слое 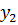 [температура
[температура 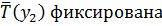 ] и т.д.
] и т.д.
Иногда проводят аналогию между 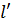 и длиной свободного пробега молекул (от соударения до соударения). Как следствие этой аналогии, величину
и длиной свободного пробега молекул (от соударения до соударения). Как следствие этой аналогии, величину 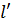 называют длиной пути смешения. Аналогично простейшим представлениям о молекулярном движении объем жидкости как бы перемещается на расстояние
называют длиной пути смешения. Аналогично простейшим представлениям о молекулярном движении объем жидкости как бы перемещается на расстояние 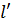 , при этом вместе с массой жидкости осуществляется перенос, в частности, энтальпии. Аналогии между молекулярным и турбулентным движениями достаточно условна. Ее достоинство заключается в наглядности. Заметим, что по смыслу турбулентного движения длина пути смешения
, при этом вместе с массой жидкости осуществляется перенос, в частности, энтальпии. Аналогии между молекулярным и турбулентным движениями достаточно условна. Ее достоинство заключается в наглядности. Заметим, что по смыслу турбулентного движения длина пути смешения 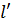 не должна быть постоянной величиной. Можно говорить о вероятностном (статическом) значении
не должна быть постоянной величиной. Можно говорить о вероятностном (статическом) значении 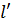 .
.
Разность 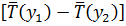 можно представить следующим образом:
можно представить следующим образом:
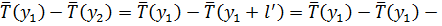
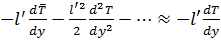 .
.
Тогда для турбулентного (пульсационного) переноса теплоты можно написать:
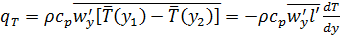 . (5.38)
. (5.38)
Исходя из предположений, аналогичных сделанным ранее, турбулентный перенос по 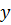 количества движения относительно оси
количества движения относительно оси 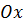 можно описать уравнением
можно описать уравнением
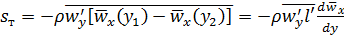 . (5.39)
. (5.39)
Таким образом, величины 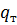 и
и 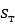 пропорциональны производным
пропорциональны производным 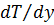 и
и 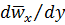 . Учитывая этот важный вывод, запишем как определения следующие уравнения:
. Учитывая этот важный вывод, запишем как определения следующие уравнения:
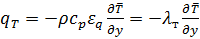 (5.40)
(5.40)
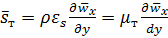 , (5.41)
, (5.41)
где 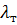 ,
, 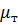 – соответственно коэффициенты турбулентного переноса теплоты и количества движения;
– соответственно коэффициенты турбулентного переноса теплоты и количества движения; 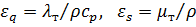 – соответственно кинематические коэффициенты турбулентного переноса теплоты и количества движения. Размерности этих коэффициентов соответствуют размерностям аналогичных коэффициентов
– соответственно кинематические коэффициенты турбулентного переноса теплоты и количества движения. Размерности этих коэффициентов соответствуют размерностям аналогичных коэффициентов 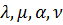 , учитывающих молекулярный перенос теплоты и количества движения.
, учитывающих молекулярный перенос теплоты и количества движения.
Коэффициенты 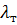 и
и 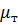 не являются физическими параметрами среды. Они зависят, как это следует из уравнений (5.40) и (5.36), (5.37), от параметров процесса и, следовательно, могут изменяться в рассматриваемом пространстве.
не являются физическими параметрами среды. Они зависят, как это следует из уравнений (5.40) и (5.36), (5.37), от параметров процесса и, следовательно, могут изменяться в рассматриваемом пространстве.
Теплота и количество движения в направлении оси 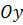 переносятся также и молекулярным механизмом. В результате можно написать:
переносятся также и молекулярным механизмом. В результате можно написать:
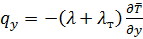 ; (5.42)
; (5.42)
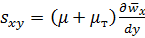 . (5.43)
. (5.43)
Сплошная твердая стенка непроницаема для поперечных пульсаций 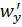 ; следовательно, при
; следовательно, при 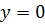 будет
будет 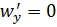 . Отсюда следует, что непосредственно на стенке
. Отсюда следует, что непосредственно на стенке 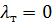 и
и 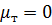 . Вдали от стенки коэффициенты турбулентного переноса
. Вдали от стенки коэффициенты турбулентного переноса 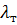 и
и 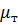 могут во много раз превышать соответственно
могут во много раз превышать соответственно 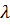 и
и 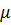 ; для этой области, напртив, можно полагать, что
; для этой области, напртив, можно полагать, что 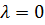 и
и 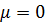 (точнее,
(точнее, 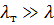 ,
, 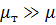 ).
).
Система уравнений турбулентного пограничного слоя. Как следует из (5.32) и (5.35), при записи уравнений в осредненных значениях скорости и температуры необходимо учитывать и турбулентный (пульсационный) перенос теплоты и количества движения. Для турбулентного пограничного слоя при принятых ранее ограничениях (см.§5.3) уравнения энергии (5.30), движения (5.28) и сплошности (5.29) могут быть записаны в следующем виде:
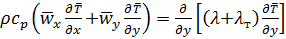 ; (5.44)
; (5.44)
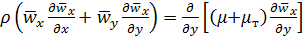 ; (5.45)
; (5.45)
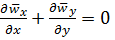 . (5.46)
. (5.46)
Здесь учтено, что турбулентный перенос в направлении оси 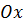 много меньше турбулентного переноса в направлении
много меньше турбулентного переноса в направлении 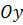 , так как
, так как 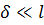 и
и 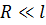 , где
, где 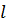 – длина пластины.
– длина пластины.
Полагают, что 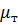 и
и 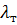 зависят от тех же факторов (переменных), от которых зависят поля осредненных скорости и температуры. Для замыкания системы дифференциальных уравнений необходимо добавить уравнения, характеризующие связь
зависят от тех же факторов (переменных), от которых зависят поля осредненных скорости и температуры. Для замыкания системы дифференциальных уравнений необходимо добавить уравнения, характеризующие связь 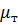 и
и 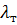 с этими переменными.
с этими переменными.
Предложено много способов, позволяющих в первом приближении замкнуть систему дифференциальных уравнений для турбулентного течения, но мы рассмотрим лишь простейший. Из уравнения (5.37)
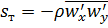
и уравнения (5.39) для одномерного турбулентного переноса
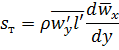
следует, что
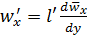 .
.
Примем, что
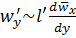 ,
,
тогда
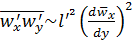 .
.
Включая коэффициент пропорциональности во вновь вводимую величину 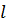 ,из (5.37) имеем[2]:
,из (5.37) имеем[2]:
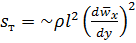 . (5.47)
. (5.47)
Величину 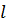 часто также называют длиной пути смешения, хотя она только пропорциональна
часто также называют длиной пути смешения, хотя она только пропорциональна 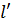 . В последнее время
. В последнее время 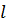 предпочитают называть масштабом турбулентности. Полагают, что
предпочитают называть масштабом турбулентности. Полагают, что 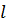 характеризует внутреннюю геометрическую структуру турбулентного потока, некоторый средний размер турбулентно перемещающихся масс жидкости. При фиксированном значении производной
характеризует внутреннюю геометрическую структуру турбулентного потока, некоторый средний размер турбулентно перемещающихся масс жидкости. При фиксированном значении производной 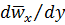 касательное напряжение турбулентного трения
касательное напряжение турбулентного трения 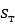 пропорционально
пропорционально 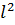 .
.
Сравнивая уравнения (5.39) и (5.47), получаем
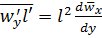 . (5.48)
. (5.48)
Подставляя последнее значение в уравнение (5.38), имеем:
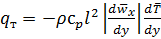 . (5.49)
. (5.49)
Формулы (5.47) и (5.49) предложены Л.Прандтлем. В пристенной области турбулентного течения масштаб турбулентности (как и турбулентный перенос количества движения и теплоты) должен уменьшаться по мере приближения к стенке из-за воздействия последней. Согласно Прандтлю
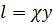 . (5.50)
. (5.50)
Как показывают измерения и расчеты, в пристенной области турбулентного течения (но в области, где молекулярным трением можно пренебречь) безразмерную величину 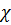 можно считать равной 0,4.
можно считать равной 0,4.
Таким образом, в первом приближении задача замкнута, значения 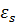 и
и 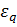 (или
(или 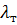 и
и 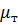 ) определены:
) определены:
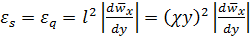 (5.51)
(5.51)
[сравнить формулы (5.40), (5.41), и (5.47), (5.49].
Формула (5.51) показывает, что существует аналогия между переносом количества движения и переносом теплоты. Формальная аналогия, следующая из (5.51), отражает концепцию, согласно которой одни и те же объемы жидкости, участвуя в пульсационном движении, переносят одновременно количество движения и теплоту и не взаимодействуют на пути 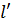 с окружающей средой. На самом деле при переносе, например, теплоты может происходить теплообмен. Пульсационный перенос количества движения может быть связан с диссипацией механической энергии из-за вязкости жидкости. Все это заставляет вносить коррективы в ранее описанную теорию, в частности вводить для описания переноса количества движения и теплоты различные значения
с окружающей средой. На самом деле при переносе, например, теплоты может происходить теплообмен. Пульсационный перенос количества движения может быть связан с диссипацией механической энергии из-за вязкости жидкости. Все это заставляет вносить коррективы в ранее описанную теорию, в частности вводить для описания переноса количества движения и теплоты различные значения 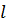 .
.
Турбулентное течение характеризуют также такими величинами, как кинетическая энергия турбулентного течения 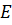 и степень турбулентности
и степень турбулентности 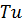 :
:
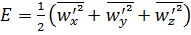 ; (5.52)
; (5.52)
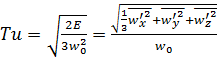 , (5.53)
, (5.53)
где 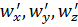 - пульсационные составляющие скорости в какой-либо точке (предельно малой области) турбулентного потока;
- пульсационные составляющие скорости в какой-либо точке (предельно малой области) турбулентного потока; 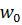 – характерная скорость процесса, например пограничного слоя за
– характерная скорость процесса, например пограничного слоя за 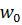 выбирают скорость набегающего потока (см. §5.3).
выбирают скорость набегающего потока (см. §5.3).
Несмотря на определенную незавершенность описанной здесь теории, она может давать приемлемые для практики результаты.
[1] Точнее, при 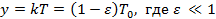 , так как температура
, так как температура 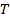 должна асимптотически стремиться к значению
должна асимптотически стремиться к значению 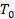 .
.
[2] Чтобы правильно определить знак 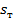 , формулу (5.47) следует записать в виде
, формулу (5.47) следует записать в виде
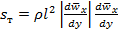 . (5.47’)
. (5.47’)
Знак 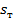 определяется знаком производной
определяется знаком производной 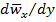 .
.
Дата добавления: 2016-06-05; просмотров: 3269;











