Просветление плазмы магнитным полем

При наложении магнитного поля на плазму электроны вращаются вокруг силовых линий магнитного поля и становятся не свободными. Во внешнем магнитном полу каждая движущаяся частица под действием силы Лоренца закручиваутся на магнитную силовую линию. Исключение составляют заряженные частицы, которые движутся вдоль силовой магнитной линии. Радиус вращения в случае движения частицы в плоскости перпендикулярной вектору магнитной индукции внешнего поля, определится из равенства центростремительной силы силе Лоренца в отсутствии внешнего электрического поля, а именно применительно к электрону как наиболее подвижной частице

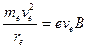, (14)

откуда 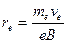. (15)

Величина r_e, определяемая равенством (15), называется ларморовским радиусом. Период обращения электрона по окружности вокруг магнитной силовой линии Т_В найдется из равенства

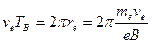. (16)

Следовательно,

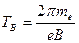(17)

и круговая частота, соответствующая этому периоду вращения равна

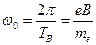. (18)

Величина ω₀ называется ларморовской частотой вращения движущейся заряженной частицы в замагниченной плазме. На этой частоте электрон должен излучать. Применительно к ионосфере частота (18) названа частотой гиромагнитного резонанса. Учитывая, что напряженность магнитного поля Земли составляет Н_З = 0,5 Эрстед = 40 А/м, поэтому гиромагнитный резонанс ионосферы составляет ~ МГц.

Радиус и частота вращения определяются соответственно по формулам (15) и (18). Так как электрон вращается вокруг силовой магнитной линии, то такой электрон можно рассматривать как некую колебательную систему. Если на такую систему направить электромагнитную волну, то на вращающийся электрон будет действовать переменная сила и тогда электрон начнет совершать вынужденные колебания, а при равенстве частот колебаний падающей электромагнитной волны и вращения электрона вокруг силовой линии магнитного поля возникнет резонанс. При резонансе частота падающей волны

, (19)

где 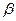- коэффициент затухания для вращающегося электрона, а - ларморовская частота .

Амплитуда колебания соответствует радиусу вращения и равна

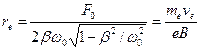. (20)

Здесь .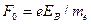

Обычно 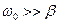, а коэффициент затухания .

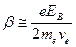При горении теплозащитного покрытия (фенольный графит) в окружающую среду испаряются в основном трехатомные молекулы углерода, для которых энергия сродства 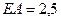эВ. В достаточно разреженной плазме при ионизации этих молекул средняя энергия электронов эВ, что соответствует температуре ~ 16 000 К, а в плотной плазме энергия электронов соответствует атомной температуре, т.е., равновесной температуре газа. Следовательно, средняя скорость электронов в плазме является постоянной величиной, а коэффициент затухания зависит только от величины электрической напряженности падающей волны, а радиус вращения электрона вокруг силовой линии магнитного внешнего поля в соответствии с (15) обратно пропорционален магнитной индукции .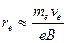

Отсюда следует: чем больше значение магнитной индукции, тем меньше радиус вращения и тем меньше вероятность столкновения электрона с окружающими частицами среды, с передачей свободным электроном энергии от волны во внутрь окружающей среды. Длина свободного пробега в плазме 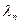вполне определенная величина. При наложении внешнего магнитного поля электрон начнет закручиваться на магнитную силовую линию. В этом случае длина свободного пробега будет уменьшаться, как это показано на рис. 6. Электрон движется в магнитном поле по окружности. На него действует центростремительная сила, определяемая силой Лоренца, которая создает центростремительное ускорение

.

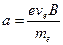Время движения электрона по окружности, равной длине свободного пробега,

.

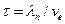Тогда вдоль оси Y-в электрон пройдет расстояние .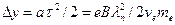

Из рис. 6 следует, что .

Тогда 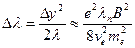. (21)

Если уменьшение длины свободного пробега электрона в плазме будет соизмеримо с радиусом вращения, то возникнет резонанс, и электромагнитная волна беспрепятственно будет проходить сквозь плазму с заметным усилением, а приближаться к резонансу будет пропорционально квадрату магнитной индукции. Поэтому величину магнитной индукции внешнего магнитного поля при заданной температуре электронной компоненты плазмы следует подбирать такую, чтобы колебания плазмы совпадали по частоте с частотой падающей электромагнитной волны.

Следовательно, величина магнитной индукции подбирается так, чтобы возникал резонанс.