Плазма и ее макроскопические свойства

Е2

В плазме присутствуют свободные отрицательные заряды с концентрацией сводных электронов n_е и в ряде случаев отрицательные ионы с концентрацией . Свободные положительные заряды – однозарядные, двухзарядные и т. д. ионы, концентрации которых обозначим соответственно 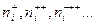Можно записать следующее приблизительное равенство 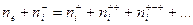(1)

Это соотношение свидетельствует о том, что плазма в целом квазинейтральна, т.е., в ней нет заметного избытка зарядов одного знака над зарядами другого знака. Такое определение плазменного состояния вещества было дано Ленгмюром в 1929 г.

При достаточно высокой температуре внутри плазмы в некоторых локальных небольших объемах за счет кинетической энергии заряженных частиц равенство (1) может нарушаться. В результате в таком объеме возникнет электрическое поле, которое своим действием на заряженные частицы будет стремиться возвратить плазму в исходное квазинейтральное состояние. Выясним эту ситуацию подробнее на примере однократно ионизированной плазмы, где .

Пусть в некотором объеме радиуса r внутри плазмы при температуре Т произошло полное разделение электрических зарядов разных знаков (рис. 2). Внутри выделенной сферы присутствуют заряды только одного знака с концентрацией 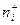. Чтобы электрону покинуть этот объем, необходимо совершить работу против сил электростатического притяжения. При удалении электрона на расстояние 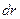совершается работа

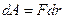. (2)

На основании закона Кулона

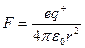, (3)

где - положительный заряд внутри выделенной сферы радиуса r. С учетом (3) получаем следующую величину работы

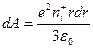. (4)

При температуре плазмы Т электрон обладает внутренней энергией поступательного движения, равной 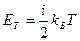(здесь i = 3 – число степеней свободы). В каждой степени свободы частица совершает движение в прямом и обратном направлении. Электрон, покидая положительно заряженную сферу радиуса r , совершает движение в одном из направлений. Поэтому он в одном из направлений обладает поступательной энергией 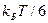. Эта энергия преодолевается силами электростатического взаимодействия. Тогда

. (5)

Отсюда максимальное расстояние, на которое электрон удалится от центра полностью положительно заряженной сферы, составит

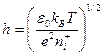. (6)

Величина h, определяемая по (6), называется дебаевским радиусом экранирования. Дебай, основываясь на некоторых упрощениях, показал, что потенциал поля точечного заряда в электролите изменяется как 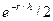, а на расстояниях r, превышающих h, электрическое поле в электролите экранируется зарядами противоположного знака. Применимость теории Дебая к плазменному состоянию не совсем оправдано, однако вывод, что дебаевский радиус является мерой расстояния, на котором концентрация электронов 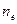может существенно отклоняться от 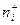не вызывает сомнений. На расстояниях больших радиуса Дебая плазма является квазинейтральной и должно выполняться условие, определяемое равенством (1). Отсюда следует, что под плазмой следует понимать такой ионизированный газ, характерные размеры которого значительно превышают радиус Дебая.

Внутри радиуса Дебая возможны отклонения от равенства (1). Такие отклонения приводят к колебаниям электронной и ионной компонент плазмы, т.е., к электростатическим колебаниям плазмы.