Кривые предельных длин отсеков

Одним из важных вопросов при проектировании судна является обеспечение непотопляемости и разделение его на отсеки с помощью поперечных водонепроницаемых переборок.

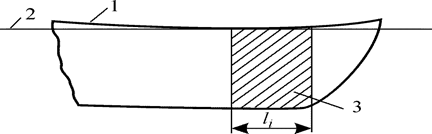
Рис. 5.6. Предельная длина отсека

1 – предельная линия погружения; 2 – аварийная ватер линия;

3 – затопленный отсек

При затоплении любого из этих отсеков или группы отсеков для транспортного судна непотопляемость считается обеспеченной, если не будет превзойден допустимый предел погружения судна и ватерлиния при аварийном погружении не окажется выше предельной линии погружения. Очевидно, что положение аварийной ватерлинии зависит от объема затопленного отсека, а для определенного судна – от длины отсека.

Предельная аварийная ватерлиния должна быть касательной к предельной линии погружения, а соответствующая этому погружению длина затопленного отсека l_i является также предельной (рис. 5.6). Следовательно, предельная длина отсека есть такое расстояние между поперечными водонепроницаемыми переборками, при котором еще удовлетворяются заданные требования к аварийной посадке. Очевидно, что каждому следу ватерлинии, касательному к предельной линии погружения, будет соответствовать затопленный отсек (группа отсеков) предельной длины.

Расчет и построение кривой предельных длин отсеков l_i(x_i) выполняют в следующей последовательности:

а) вычисляют и строят кривую предельных объемов отсеков v_i(x_i);

б) строят строевую по шпангоутам для предельной линии погружения;

в) рассчитывают и строят интегральную кривую строевой по шпангоутам;

г) определяют графически предельные длины отсеков.

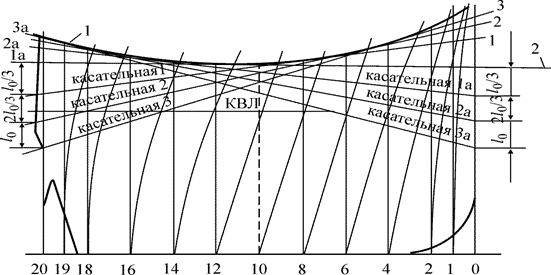
Рис. 5.7. Построение касательных к предельной линии погружения

1 – предельная линия погружения; 2 – касательная к предельной линии погружения в нижней ее точке

Для вычисления предельных объемов отсеков следует для каждой аварийной ватерлинии с помощью масштаба Бонжана найти площади погруженных частей шпангоутов, а затем по правилам приближенного интегрирования определить объемное водоизмещение и абсциссу для каждой ватерлинии. Число аварийных ватерлиний на масштабе Бонжана определяется числом точек, необходимых для построения кривой предельных объемов. Обычно принимают нечетное число ватерлиний (7 или 9): одна горизонтальная – в районе миделя, носовые и кормовые – через равные промежутки (рис. 5.7). Для каждой ватерлинии вычисляют водоизмещение V_i и объем затапливаемого отсека v_i:

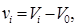(5.57)

где V₀ – водоизмещение по начальную ватерлинию до затопления. Абсциссу x_i ЦТ объема затопленного отсека определяют из уравнения статических моментов

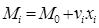(5.58)

(M₀ – статический момент объема V₀ относительно плоскости yOz; M_i – статический момент объема V_i относительно плоскости yOz):

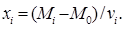(5.59)

Таким образом, на основании формул (5.57) и (5.59) в зависимости от числа выбранных аварийных ватерлиний находят предельные объемы v_i и соответствующие им абсциссы x_i, по значениям которых легко построить зависимость v_i(x_i) – кривую предельных объемов. Чтобы найти предельные длины отсеков необходимо на строевой по шпангоутам, соответствующей данной аварийной ватерлинии, двумя ординатами выделить площадь, равную предельному объему, чтобы ЦТ этой площади отстоял от мидель-шпангоута на расстоянии x_i. Такие построения выполняют столько раз, сколько принято аварийных ватерлиний.

Однако для большинства судов продольная кривизна палубы переборок невелика, т. е. касательная и предельная линии погружения на значительном участке совпадают. Поэтому для упрощения расчетов строевую по шпангоутам строят для предельной линии погружения. Далее строят интегральную кривую строевой по шпангоутам, ординаты которой находят по формуле

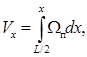(5.60)

где V_x – переменный объем, отсчитываемый от носового перпендикуляра до некоторого поперечного сечения с абсциссой x; 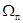– площадь погруженной части шпангоута до предельной линии погружения.

Для построения кривой предельных длин отсеков на одном графике вычерчивают строевую по шпангоутам для предельной линии погружения, кривую предельных отсеков и интегральную кривую.

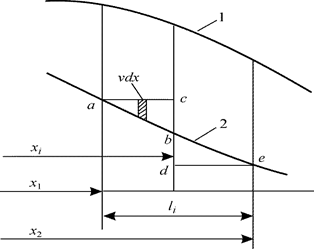
Рис. 5.8. Построение кривых предельных длин

1 – строевая по шпангоутам; 2 – интегральная кривая

Для выбранного положения ЦТ отсека (абсциссы x_i) по кривой предельных объемов находят предельный объем v_i. На графике интегральной кривой проводят две ординаты таким образом, чтобы их разность в масштабе была равна предельному объему, а статический момент объема относительно ординаты, проходящей через его ЦТ, был бы равен нулю, т. е. так, чтобы абсцисса ЦТ отсека была равна x_i. Легко показать, что площади acb и bde (рис. 5.8) представляют собой статические моменты объемов относительно cd. Рассмотрим произведение vdx, которое представляет собой элементарный статический момент. Тогда полный статический момент 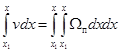равен всей площади acb.

Аналогичный вывод можно сделать и для площади bde. Подбирая обе эти площади так, чтобы они были равны, находят абсциссу ЦТ предельного объема отсека x_i. Очевидно, что сумма отрезков ac и de представит собой предельную длину отсека. Проводя аналогичные рассуждения для всех 7 (или 9) предельных объемов, определяют 7 (или 9) предельных длин отсеков (рис. 5.9).

Кривую предельных длин отсеков строят в прямоугольной системе координат, в которой на оси абсцисс в масштабе длины судна наносят абсциссы середин отсеков, а на оси ординат – предельную длину отсека.

На рис. 5.10 представлена теоретическая кривая предельных длин отсеков (кривая 1), построенная без учета внутреннего насыщения отсеков (объема конструкций, грузов, трубопроводов, механизмов и другого оборудования).

Крайние точки кривой (A и B) соответствуют кормовому носовому положениям отсеков предельной длины. При этом очевидно, что отстояние середины длин отсеков от носового и кормового теоретических шпангоутов равны половине предельной длины. Поэтому легко найти углы наклона ограничивающих прямых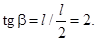

Для учета внутреннего насыщения отсека вводится понятие о коэффициенте проницаемости или коэффициенте затопления, который представляет собой отношение объема поступившей в отсек воды к теоретическому объему отсека.

Коэффициенты проницаемости отсеков различного назначения судов разных типов определяют расчетным путем на основании данных о внутреннем насыщении. Коэффициенты проницаемости больших отсеков, в пределах которых располагаются помещения различных типов, необходимо вычислять как средние.

Значения коэффициентов 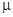для помещений различного на значения приведены ниже.

· Помещения, занятые механизмами, электростанциями, технологическим

оборудованием промысловых судов - 0,85;

· Помещения непассажирских судов, занятых грузами или запасами - 0,60;

· Жилые помещения; помещения, не занятые существенным количеством грузов;

· помещения, занятые колесной техникой - 0,95;

· Пустые цистерны, цистерны для балластировки забортной водой - 0,98;

· Грузовые помещения накатных судов - 0,80;

· Грузовые помещения с грузом в контейнерах, трейлерах, грузовиках - 0,71;

· Помещения для жидких грузов (кроме нефтеналивных судов, химовозов и

газовозов), жидкого балласта - 0,95;

· Помещения, занятые лесным грузом - 0,35;

· Помещения, занятые рудой - 0,80.

Учет внутреннего насыщения отсека, т. е. коэффициента проницаемости, дает возможность увеличить предельный объем отсека и предельную его длину. Действительная длина отсека 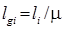больше теоретической его длины, поскольку 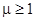. Так как коэффициенты проницаемости отсеков по длине судна существенно отличаются, то кривая действительных предельных длин отсеков состоит из отдельных участков, как показано на рис. 5.10.

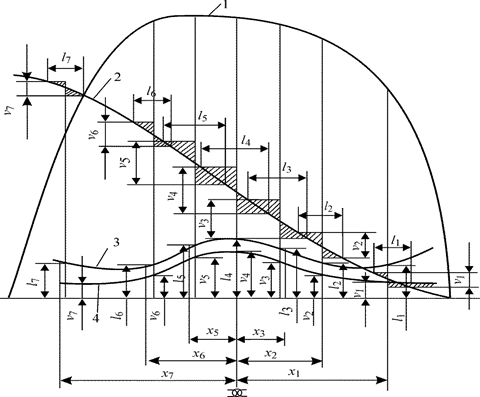
Рис. 5.9. Кривые предельных длин и предельных объемов отсеков

1 – строевая по шпангоутам до предельной линии погружения; 2 – интегральная кривая; 3 – кривая предельных длин отсеков; 4 – кривая предельных объемов отсеков

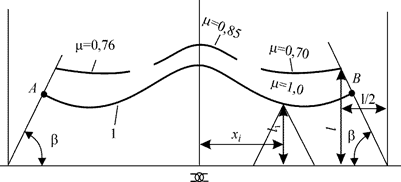
Рис. 5.10. Кривые предельных длин отсеков без и с учетом внутреннего насыщения

При проектировании судна поперечные водонепроницаемые переборки располагаются с учетом конструктивных соображений, однако во всех случаях длина водонепроницаемого отсека должна быть не более предельной длины. Это требование проверяют на кривой предельных длин отсеков. На оси абсцисс наносят фактические длины отсеков, и строят равнобедренные треугольники, высота которых равна длине отсека. Если вершина этого треугольника располагается ниже кривой предельных длин или ее касается, то при затоплении отсека аварийная ватерлиния будет ниже или касательна к предельной линии погружения, в противном случае необходимо изменить расстояние между переборками.

Кривая предельных длин отсеков позволяет также построить кривую допустимых длин, ординаты которой могут быть получены умножением ординат первой кривой на коэффициент безопасности, меньший единицы. Коэффициент безопасности называется фактором подразделения. Он зависит от длины судна и характера его эксплуатации. В случае если фактор подразделения равен 1; 0,5; 0,33, судно остается на плаву, а аварийная ватерлиния остается касательной к предельной линии погружения при затоплении одного, двух или трех смежных отсеков.