Способ исключения отсека (способ постоянного водоизмещения)

Рассмотрим отсек категории 2б, сообщающийся с забортной водой и открытый сверху. Пусть судно до затопления отсека плавало прямо и на ровный киль по ватерлинию В₀Л₀, а соответствующие этой ватерлинии элементы судна следующие: V – объемное водоизмещение; T – осадка; x_c и z_c – координаты ЦВ; S – площадь ватерлинии; I_x, I_f – моменты инерции площади относительно главных центральных осей; x_f – абсцисса ЦТ площади ватерлинии; но h₀ и H₀ – поперечная и продольная метацентрические высоты. Предположим, что все грузы раскреплены и в процессе наклонения положение ЦТ неизменно, а борта судна в районе изменения осадки прямостенные.

Допустим, что затоплен отсек правого борта (рис. 5.3), при этом изменились: средняя осадка судна, углы крена и дифферента, метацентрические высоты. В соответствии с идеей способа объем воды, влившейся в отсек по новую ватерлинию В₁Л₁, исключим из объема погруженной части корпуса, а для восстановления условия равновесия в воду должен войти объем корпуса судна между двумя ватерлиниями, равный v₁. Так как отсек открыт сверху, часть объемов 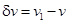являются общими и из рассмотрения могут быть исключены.

Таким образом, при погружении произошло как бы перемещение объема v, и форма погруженной части изменилась при сохранений значения объемного водоизмещения. Такое изменение формы погруженной части корпуса приведет к перемещению ЦТ погруженного объема, т. е. ЦВ. Кроме того, вследствие наклонения корабля (крена и дифферента) координаты ЦВ получат дополнительное приращение.

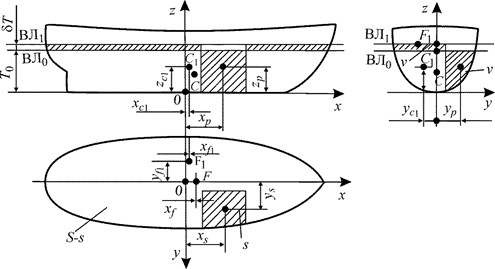
Рис. 5.3. К расчету непотопляемости способом исключения отсека

Расчет непотопляемости в данном случае заключается в определении посадки и остойчивости судна в предположении об изменении формы погруженной части корпуса при постоянном водоизмещении.

В соответствии с рис. 5.3 введем обозначения: δT – изменение средней осадки при затоплении отсека; s – потерянная площадь ватерлинии; S – s – площадь поврежденной ватерлинии; v – объем воды, влившейся в отсек по начальную ватерлинию В₀Л₀; 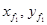– координаты ЦТ поврежденной ватерлинии; 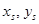– координаты ЦТ площади потерянной ватерлинии; 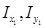– моменты инерции площади поврежденной ватерлинии относительно центральных осей, проходящих через ЦТ площади поврежденной ватерлинии; 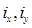– собственные моменты инерции потерянной площади ватерлинии.

Найдем элементы судна после затопления отсека.

Изменение средней осадки с учетом предположения о прямостенности борта равно

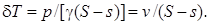(5.9)

Координаты ЦТ поврежденной ватерлинии и соответствующие моменты инерции можно определить на основании известных теорем о статических моментах и моментах инерции: статический момент суммы площадей относительно какой-либо оси равен сумме статических моментов ее составляющих относительно той же оси; момент инерции суммы площадей относительно какой-либо оси равен сумме собственных и переносных моментов инерции. Составим сначала уран нения статических моментов:

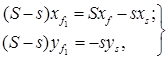(5.10)

откуда найдем координаты ЦТ площади поврежденной ватерлинии:

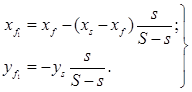(5.11)

Моменты инерции (осевые и центробежные) площади поврежденной ватерлинии относительно осей Ox и Oy проходящих через точку F₁ равны

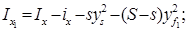(5.12)

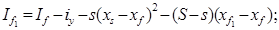(5.13)

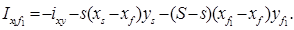(5.14)

После подстановки в формулы (5.12) – (5.14) значений координат ЦТ площади поврежденной ватерлинии согласно (5.11) выражения для моментов инерции площади поврежденной ватерлинии приобретают вид

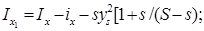(5.15)

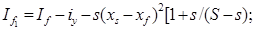(5.16)

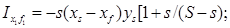(5.17)

Формула (5.17) выведена на основании допущения о том, что несимметрия потерянной площади ватерлинии относительно собственной продольной оси невелика, и центробежным моментом инерции i_xy можно пренебречь. С помощью формул (5.15) и (5.16) легко определить по перечный и продольный метацентрические радиусы судна после за топления отсека:

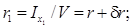
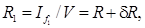
а также их изменения:

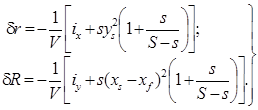(5.18)

Перейдем к определению координат ЦВ судна после затопления отсека. Как указывалось выше, приращение каждой координаты ЦВ состоит из двух составляющих;

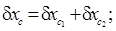
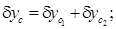
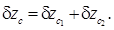(5.19)

В правых частях формул (5.19) первые члены определяют перемещение ЦВ судна, вызванное перемещением части погруженного объема в предположении отсутствия крена и дифферента, а вторые – изменение координат ЦВ, вызванное наклонением судна.

Найдем сначала первые составляющие. Как видно из рис. 5.3, исключенный объем v компенсируется объемом 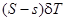, иначе говоря, объем v как бы перемещается на расстояния 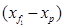, , 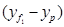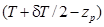. В соответствии с известной нам теоремой статических моментов получим

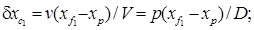(5.20)

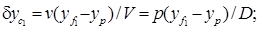(5.21)

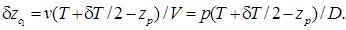(5.22)

Для приведения формул (5.20) и (5.21) к окончательному расчетному виду подставим в них в соответствии с выражениями (5.11) значения координат ЦТ поврежденной ватерлини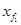и и 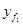. После преобразований получим

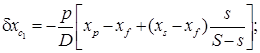(5.23)

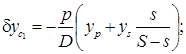(5.24)

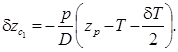(5.25)

Вторые составляющие приращений координат ЦВ обусловлены наклонением корабля, т. е. перемещением ЦВ. Для определения этих приращений воспользуемся формулами (2.14а) и (2.15), однако в качестве осей наклонения примем ос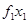и и 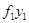, проходящие через ЦТ площади поврежденной ватерлинии:

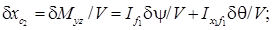(5.26)

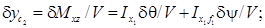(5.27)

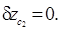(5.28)

Суммируя (5.23) и (5.26), (5.24) и (5.27) с учетом (5.25), получим полные приращения координат ЦВ, учитывающие затопление отсека и по следующее наклонение:

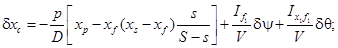(5.29)

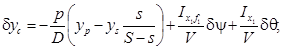(5.30)

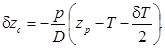(5.31)

Для определения новых значений метацентрических высот воспользуемся общими условиями равновесия (1.24) и (1.25):

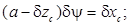(5.32)

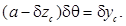(5.33)

После подстановки в (5.23) и (5.24) формул (5.32) и (5.33) с учетом (5.19) в результате преобразований получим

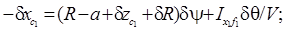(5.34)

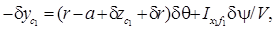(5.35)

где ;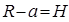

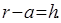
В соответствии с общей формулой для метацентрических высот их изменения могут быть представлены в виде

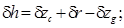(5.36)

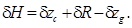(5.37)

При решении задачи способом постоянного водоизмещения изменение аппликаты ЦТ равно нулю. С учетом (5.34) и (5.35) формулы для изменения метацентрических высот легко записать в виде

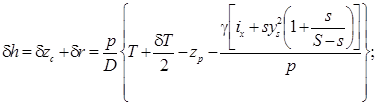(5.38)

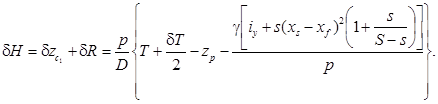(5.39)

Приращения 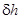и 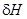отнесены к водоизмещению неповрежденного корабля и пропорциональны приращениям соответствующих коэффициентов остойчивости.

Выражения для определения углов крена и дифферента могут быть найдены из решения системы

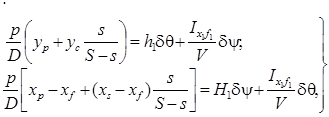(5.40)

которая получена после подстановки в левые части уравнений (5.23) и (5.24) выражений (5.34) и (5.35). Для упрощения задачи можно считать, что главные центральные оси поврежденной ватерлинии с площадью S – s параллельны осям Ox и Oy, тогда 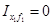и система уравнений для определения углов крена и дифферента разделится. Если, кроме того, положить, что x_p = x_s и y_p = y_s, т. е. ЦТ потерянной площади ватерлинии лежит на одной вертикали с ЦТ объема отсека, то

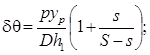
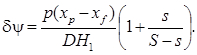(5.41)

Формулы (5.41) дают возможность рассчитать изменение остойчивости и посадки при затоплении отсека способом постоянного водоизмещения. Сравнивая эти результаты с результатами расчета непотопляемости методом переменного водоизмещения, отметим, что значения величин, характеризующих положение корабля после затопления отсека, таких, как средняя осадка, углы крена и дифферента, а также коэффициентов остойчивости, определяющих восстанавливающие моменты, не зависят от способа расчета. Что же касается других величин, например метацентрических высот, то их значения, найденные двумя разными способами, различны.

Проведем некоторые сопоставления. Рассмотрим изменение средней осадки. На основании формул (5.1) и (5.9) имеем

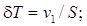
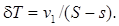(5.42)

Из рис. 5.4 видно, что 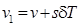. Подставим это выражение в первую из формул (5.42). Тогда получим, что 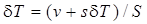, или 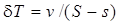, т. е. первая и вторая формулы (5.42) дают одинаковые значения .

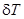Можно также априори считать, что значения восстанавливающих моментов, а также углов крена и дифферента не зависят от способа расчета. Тогда

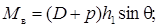
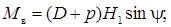(5.43)

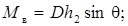
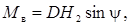(5.44)

т. е. 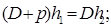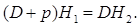(5.45)

Таким образом, коэффициенты остойчивости, вычисленные двумя различными способами, равны между собой. Из этого условия следует, что метацентрические высоты h₁ и H₁, определенные способом переменного водоизмещения, меньше метацентрических h₂ и H₂, найденных способом постоянного водоизмещения.