Проверка влияния интегрирующей цепи на коэффициенты ряда Фурье.

2.1. Ограничьтесь при моделировании сигнала четырьмя гармониками.

2.2. Пропустите сигнал с функционального генератора на осциллограф через интегрирующую цепь с указанной в табл. 5.1 постоянной времени.

2.3. Используя комплексный метод, рассчитайте коэффициенты передачи сигнала через интегрирующую цепь на частотах используемых вами генераторов и определите величины фазовой задержки при этом. Установите другие значения амплитуд используемых генераторов с учетом влияния интегрирующей цепи. Учтите при этом и влияние фазовой задержки путем вычитания из установленной фазы в 90º рассчитанного для текущей частоты значения фазы.

2.4. Подав питание, убедитесь, что вы правильно рассчитали все параметры коррекции с учетом влияния интегрирующей цепи. Если ваши расчеты и выполненные установки правильны, то вы увидите, что ваша модель хорошо подменяет моделируемый сигнал.

Контрольные вопросы

1. Проверьте справедливость утверждения, что среднее значение для выбранного сигнала равно половине амплитуды.

2. Можете ли вы объяснить отсутствие синусоидальных гармоник в ряде Фурье для выбранной функции?

3. Объясните, почему все генераторы в схеме 5.2 соединены последовательно.

4. Почему символом + генераторы подключены указанным образом, а не наоборот?

5. От чего зависит точность модели сигнала при использовании ряда Фурье?

6. Можно ли было не изменять параметры генераторов при использовании интегрирующей цепи, а использовать еще одну такую же цепь, и как ее при этом включить?

Изучение методов модуляции
электрических сигналов

Модуляция – наложение информационного сигнала на несущий сигнал. В качестве несущего сигнала может выступать гармонический или импульсный сигнал. На каждый параметр несущего сигнала можно наложить информационный, обеспечив зависимость параметра от амплитуды информационного сигнала. Параметрами гармонического сигнала являются амплитуда, частота и фазовая задержка. Это позволяет определить три разновидности модуляции гармонического сигнала: амплитудная, частотная и фазовая. Подобные варианты можно определить и для импульсного несущего сигнала, которые при этом называют амплитудно-импульсной, частотно-импульсной и фазоимпульсной модуляциями. Кроме названных разновидностей, существует множество других видов, среди которых интерес представляет широтно-импульсная модуляция, находящая широкое применение.

В данной работе обратим внимание на амплитудную и частотную модуляции (при гармонической несущей) и на широтно-им-пульсную модуляцию.

При амплитудной модуляции полезный сигнал накладывается на амплитуду гармонической несущей с частотой ω₀ следующим образом:

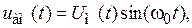
где – зависящая от полезного, модулирующего сигнала s(t) амплитуда. Коэффициент M определяет глубину модуляции и лежит в диапазоне от 0 до 1.

Рассмотрим случай, когда в качестве модулирующего сигнала выступает гармонический сигнал с частотой Ω << ω₀:

.

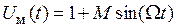Результирующий сигнал будет равен

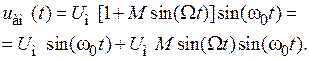
Из тригонометрии известно, что

.

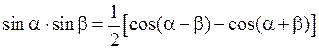Используя это выражение, получим:

.

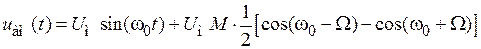Таким образом, результирующий сигнал содержит три гармоники с разными частотами и амплитудами: синусоидальный сигнал с несущей частотой и две гармоники, расположенные симметрично относительно частоты несуще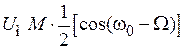й:

и .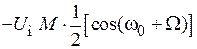

Используя три генератора синусоидальных и косинусоидальных сигналов, можно смоделировать амплитудно-модулированный сигнал. Для этого достаточно просуммировать сигналы со всех генераторов, амплитуды и фазы которых разумно определены. Суммирование можно осуществить, последовательно включив эти генераторы. Можно использовать только генераторы синусоидального сигнала, если косинусоидальные гармоники сформировать с помощью синусоидальных генераторов, включив фазовый сдвиг в аргументы информативных гармоник следующим образом:

, .

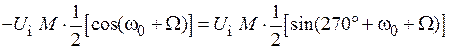Сигнал с частотной модуляцией при синусоидальном информационном сигнале может быть описан следующим уравнением:

,

где – индекс частотной модуляции, который определяет девиацию 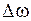, т.е. изменение несущей частоты ω относительно исходного значения.

При широтно-импульсной модуляции от текущего значения информационного сигнала зависит длительность импульса, а частота импульсного сигнала остается постоянной. Один из вариантов формирования сигнала с широтно-импульсной модуляцией может быть реализован с помощью аналогового компаратора и вспомогательного генератора пилообразного сигнала (рис. 6.1).

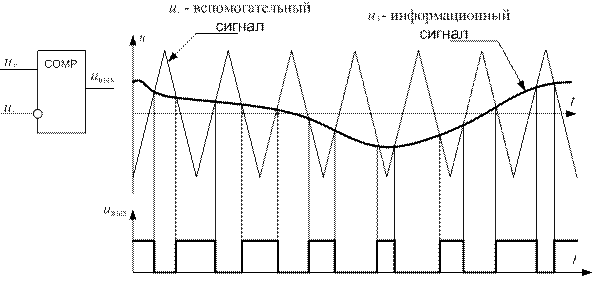
Рис. 6.1. Возможный вариант формирования цифрового сигнала
с широтно-импульсной модуляцией

Частота вспомогательного сигнала должна быть на несколько порядков выше частоты входного аналогового сигнала, несущего информацию. Если ставится задача обратного преобразования широтно-модулированного сигнала в аналоговый, достаточно использовать интегрирующую цепь с постоянной времени, значительно превышающей период несущего импульсного сигнала.

Порядок выполнения работы. Лабораторная работа выполняется на компьютере. Программа «Electronics Workbench» содержит модели генераторов, формирующих сигнал с амплитудной и частотной модуляцией, условные обозначения которых показаны на рис. 6.2. В качестве компаратора следует выбрать операционный усилитель с идеальными характеристиками, который формирует на выходе двухполярный сигнал.

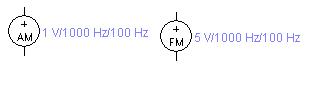
Рис. 6.2. Модели генераторов модулированных сигналов