Изучение свойств параллельного колебательного контура (резонанс токов).
|
|
добротность Q, полосу пропускания S, коэффициент прямоугольности Kп. Сравнить частотные характеристики параллельного контура с характеристиками последовательного контура.
4.1. На рабочем поле соберите схему исследования (рис. 4.10). Параметры элементов контура и генератора установите по вариантам табл. 4.3.

Рис. 4.10. Схема эксперимента
Таблица 4.3
| Вариант | C, пФ | L, мГн | Rген, МОм | R0, кОм |
| 1,6 | ||||
| 1,8 | ||||
| 0,73 | ||||
| 0,73 | ||||
| 0,73 | ||||
| 1,8 | ||||
| 1,6 | ||||
| 0,68 | ||||
| 0,68 | ||||
| 0,68 |
Настроить измеритель по осям Y и X: включить линейный масштаб, а предельные значения F и I по каналам подобрать так, чтобы характеристика размещалась в пределах экрана. Пример измерения АЧХ показан на рис. 4.11.
Провести измерение по точкам f, Ku(f), j(f) путем перемещения визирной линии по всей характеристике. Результаты измерений записать в таблицу, аналогичную табл. 4.2.
По результатам измерений построить АЧХ и ФЧХ. Показать на графиках граничные частоты fн, fвна уровне 0.7 и 0.1 от Kmax.

Рис. 4.11. Пример измерения АЧХ
Сравнить частотные характеристики параллельного контура с характеристиками последовательного контура по f0, Q, S, и Kппри одинаковых параметрах элементов L, C.
Контрольные вопросы
1. Дайте определение явления резонанса в электрической цепи. Виды резонанса.
2. Запишите параметры последовательного и параллельного колебательных контуров.
3. Как влияют Rг и Rн на параметры контура?
4. Как производится расчет АЧХ и ФЧХ коэффициента передачи по напряжению последовательного контура? Объясните форму характеристик.
5. Как определить параметры контура f0, fн,fв, S, Kп по частотным характеристикам?
6. Как отличаются по параметрам последовательный и параллельный контуры?

Моделирование электрических сигналов
с помощью ряда Фурье
В зависимости от контролируемого физического процесса, являющегося источником аналогового сигнала, поведение формируемого электрического сигнала s(t) может быть произвольным. Возникает вопрос: какими параметрами характеризовать эти процессы, чтобы можно было сравнить их между собой при необходимости, какие требования следует предъявить к аппаратуре записи этих сигналов с целью обработки, преобразования или воспроизведения с требуемой точностью? Практика показала, что наилучшим способом описания сигналов по ряду причин является применение рядов и интегралов Фурье (Жан Батист Жозеф Фурье (1768–1830) – французский математик и физик). Аппроксимация или приближенное описание исходного сигнала осуществляется с помощью гармонических сигналов с разными амплитудами, частотами и фазовыми задержками. В зависимости от того, является ли исходный сигнал периодическим или нет, для аппроксимации используют ряд или интеграл Фурье. В лабораторной работе для моделирования периодического сигнала с периодом T используется ряд Фурье. Исходный сигнал представляется в виде суммы синусоидальных и косинусоидальных гармоник с кратными частотами:
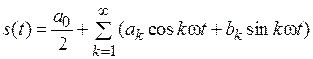 ,
,
где 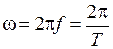 – угловая частота первой гармоники при использовании ряда Фурье; k – номер гармоники;
– угловая частота первой гармоники при использовании ряда Фурье; k – номер гармоники; 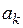 и
и 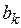 – коэффициенты ряда.
– коэффициенты ряда.
Для расчета коэффициентов 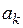 и
и 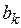 используем следующие формулы:
используем следующие формулы:
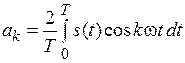 при k = 0, 1, 2, 3, …,
при k = 0, 1, 2, 3, …,
 при k = 1, 2, 3, ….
при k = 1, 2, 3, ….
Применим ряд Фурье для моделирования периодического сигнала, предложенного на рис. 5.1. Для этого сигнала можно записать выражение:
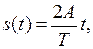 если 0 ≤ t ≤ T / 2,
если 0 ≤ t ≤ T / 2,
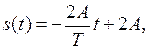 если T / 2 ≤ t ≤ T.
если T / 2 ≤ t ≤ T.
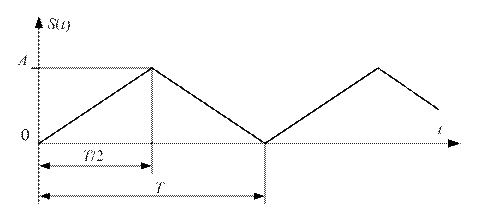
Рис. 5.1. Периодический сигнал, подлежащий моделированию
с помощью ряда Фурье
С учетом этого выражения рассчитаем коэффициенты при косинусоидальных гармониках:
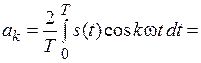
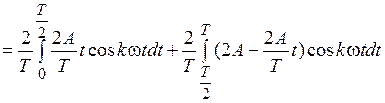 .
.
Учитывая табличные интегралы:
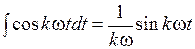 и
и 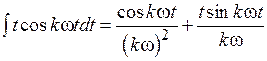 , а
, а 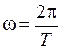 , после преобразований получим:
, после преобразований получим:
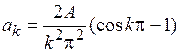 .
.
Можно заметить, что при четных значениях k величина 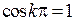 и выражение в скобках равно нулю, а при нечетных значениях k выражение в скобках равно –2. Коэффициенты bk при синусоидальных гармониках будут равны нулю, постоянная составляющая сигнала равна A/2 и ряд Фурье, соответствующий предложенной функции, будет выглядеть следующим образом:
и выражение в скобках равно нулю, а при нечетных значениях k выражение в скобках равно –2. Коэффициенты bk при синусоидальных гармониках будут равны нулю, постоянная составляющая сигнала равна A/2 и ряд Фурье, соответствующий предложенной функции, будет выглядеть следующим образом:
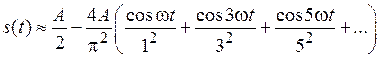
при k = 1, 3, 5, 7, 9, …. (5.1)
Количество используемых гармоник определяет величину погрешности при замене исходной функции на ряд Фурье.
Дата добавления: 2021-12-14; просмотров: 434;











