Комплексное входное сопротивление контура

Z(jw) = r(w) + jx(w) = R + j(wL – 1/wC),

где r(w) = R_Lпосл+ R_Спосл– активное сопротивлениепотерь контура, состоящее из сопротивлений потерь индуктивной катушки и конденсатора; x(w) = x_L(w) + x_C(w) = wL – 1/wC – реактивное сопротивление контура.

Если частота входного гармонического сигнала e(t) = E_mcos(wt + + y_n) примет определенное значение

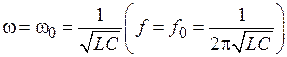, (4.1)

при котором реактивное сопротивление цепи обращается в ноль, то в контуре возникает резонанс напряжений, сопровождающийся увеличением тока в контуре.

На резонансной частоте модуль сопротивления емкости равен модулю сопротивления индуктивности

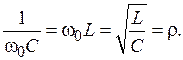
Эта величина

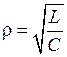(4.2)

называется характеристическимсопротивлением контура.

Амплитуды тока и напряжения реактивных элементов контура на резонансной частоте равны

.

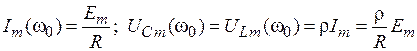Отношение напряжения на реактивном элементе к напряжению на сопротивлении потерь R на резонансной частоте называетсядобротностьюконтура:

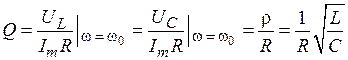, т.е. 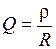. (4.3)

Величина d = 1/Q называется затуханием.

Комплексный коэффициент передачи контура по напряжению K_C(jw) для случая, когда напряжение снимают с емкости:

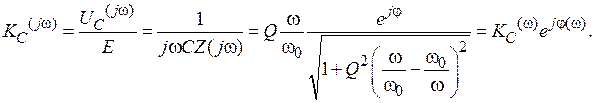
Выражение амплитудно-частотной характеристики (АЧХ) коэффициента передачи:

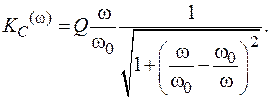(4.4)

Выражение фазочастотной характеристики (ФЧХ):

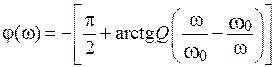. (4.5)

Максимум зависимости K_С(w) соответствует частоте w_С, назы-ваемой частотойсобственныхколебаний:

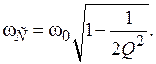
При Q > 1w_С » w₀. Например, при Q = 5, w_С = 0,99w₀.

На рис. 4.2 показаны частотные характеристики коэффициента передачи по напряжению последовательного контура.

Рис. 4.2. Частотные характеристики последовательного контура

Важнейшей особенностью колебательного контура является способность выделять из суммы гармонических колебаний различных частот входного сигнала те колебания, частота которых лежит вблизи резонансной частоты. Это свойство называется избирательностьюцепи.

Принято считать, что контур пропускает сигналы в определенном диапазоне частот, называемом полосойпропускания. В идеальном случае выходной сигнал избирательной цепи в пределах полосы пропускания должен иметь постоянное значение и быть равным нулю за пределами полосы пропускания.

Нормированная АЧХ идеальной избирательной цепи должна иметь прямоугольную форму (кривая 1 на рис. 4.3). АЧХ реальных избирательных цепей, в том числе и АЧХ колебательного контура (кривая 2 на рис. 4.3), отличаются от прямоугольной формы отсутствием резкой границы между диапазоном пропускаемых и подавляемых частот.

Рис. 4.3. Нормированные АЧХ идеальной (1) и реальной (2) цепи

Полосапропускания реальных избирательных цепей определяется как диапазон частот S = w_В – w_Н, в пределах которого амплитуда выходного сигнала не падает ниже уровня 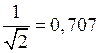от максимального значения (см. рис. 4.3).

Избирательные свойства контура определяются формой АЧХ, в частности, крутизной склонов АЧХ. Чем ближе она к прямоугольной форме, тем выше избирательность (см. рис. 4.3).

Количественно избирательность можно оценить коэффициентомпрямоугольности

Kп = Sα₁/ Sα₂,α₁ > α₂,

где Sα₁ – полоса пропускания на уровне 1/ α₁; Sα₂ – полоса пропускания на уровне 1/α₂.

Принято в технике считать 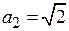, , 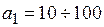т.е. полоса пропускания оценивается на уровне ≈ 0,707 и (0,1 ÷ 0,01) от максимального значения коэффициента передачи. Нижний уровень может уточняться в сторону увеличения, например, ≈ 0,1.

На границах полосы пропускания модуль коэффициента передачи колебательного контура K_С(w_В, w_Н) = 0,707K_С(w₀), а граничные частоты определяются параметрами контура w₀ и Q и не зависят от емкости C:

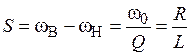. (4.6)

Чем больше Q, тем ýже полоса пропускания.