Сравнение производительности

Очевидно, что при выборе стратегии планирования критическим становится вопрос производительности. Однако точное сравнение стратегий невозможно в силу того, что относительная производительность зависит от ряда факторов, включая распределение времени обслуживания различных процессов, эффективность планирования и механизм переключения контекстов, а также природу запросов к устройствам ввода-вывода и их производительность. Тем не менее мы попытаемся сделать хотя бы самые общие выводы.

Анализ очередей

В этом разделе мы используем основные формулы, описывающие работу очередей, в предположении запуска процессов в соответствии с распределением Пуассона и экспоненциального времени обслуживания.³

³ Подробнее с терминологией, связанной с очередями, можно познакомиться во втором приложении к данной главе; материалы по анализу очередей можно найти по адресу: http://WilliamStallings.com/StudentSupport.html.

Сначала мы заметим, что любая стратегия планирования, которая выбирает очередной обслуживаемый процесс независимо от времени обслуживания, подчиняется следующему соотношению:

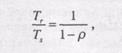
где

Т_r — время оборота (общее время пребывания в системе, ожидания плюс выполнения);

Т_s — среднее время обслуживания (среднее время нахождения в состоянии выполняющегося процесса);

r — степень использования процесса.

В частности, планирование с использованием приоритетов, при котором приоритет каждому процессу назначается независимо от ожидаемого времени обслуживания, обеспечивает то же среднее время оборота, что и простейшая стратегия FCFS. Более того, эти средние значения не зависят от наличия или отсутствия вытеснения.

За исключением стратегий FCFS и RR, рассматривавшиеся стратегии планирования осуществляют выбор процесса с учетом ожидаемого времени обслуживания. К сожалению, очень сложно разработать точные аналитические модели этих стратегий. Однако мы можем попытаться рассмотреть относительную производительность стратегий — в сравнении со стратегией FCFS, рассматривая приоритетное планирование, в котором приоритет основан на времени обслуживания.

Если планирование выполняется с учетом приоритетов и если классы приоритетов процессам назначаются на основе времени обслуживания, выявляются определенные отличия разных стратегий. В табл. 9.6 приведены формулы, получающиеся при использовании двух классов приоритетов с различным временем обслуживания для каждого класса. Я в таблице обозначает частоту поступления новых процессов в систему. Приведенные результаты могут быть обобщены для произвольного количества классов приоритетов. Обратите внимание, что для не вытесняющего и вытесняющего планирования получаются разные результаты. При вытесняющем планировании предполагается, что низкоприоритетный процесс немедленно прерывается, как только становится готов к выполнению процесс с более высоким приоритетом.

Таблица 9.6. Формулы для двух классов приоритетов

Предположения:	а) Общие формулы:
Поступление новых процессов подчиняется распределению Пуассона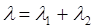
Процессы с приоритетом 1 обслуживаются перед процессами с приоритетом 2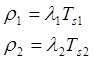
Для процессов с равным приоритетом применяется стратегия "первым вошел — первым вышел"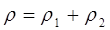
Во время обслуживания процессы не прерываются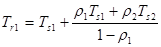
Процессы не покидают очередь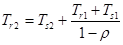
б) Экспоненциальное время обслуживания, прерывания отсутствуют	в) Экспоненциальное время обслуживания с наличием вытеснения

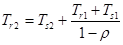
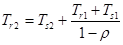
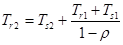
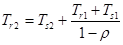
В качестве примера рассмотрим случай с двумя классами приоритетов, равным количеством поступающих в систему процессов каждого класса и средним временем обслуживания низкоприоритетного класса, в 5 раз превышающим время обслуживания высокоприоритетного класса. Тем самым мы хотим отдать предпочтение коротким процессам. На рис. 9.11 показан общий результат. При предпочтении коротких процессов среднее нормализованное время оборота уменьшается. Как и следовало ожидать, результат еще лучше при использова­нии вытеснения. Обратите, однако, внимание на то, что на общую производи­тельность это влияет не так сильно.

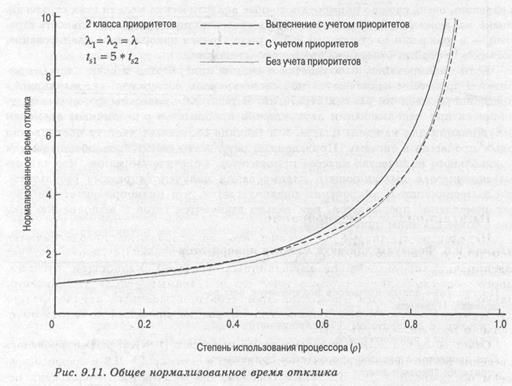
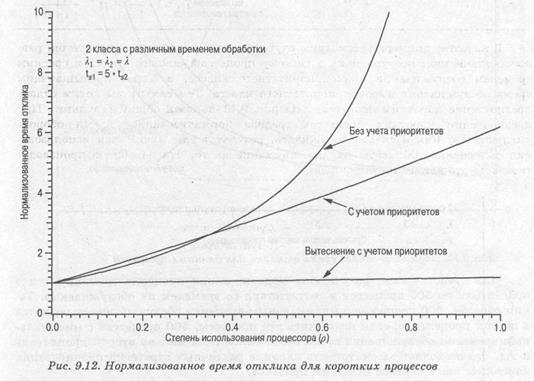
Однако при отдельном рассмотрении классов приоритетов наблюдаются значительные отличия. На рис. 9.12 показаны результаты для коротких процессов с высоким приоритетом. Для сравнения верхняя кривая на графике построена в предположении, что приоритеты не используются, и мы просто рассматриваем относительную производительность той половины процессов, продолжительность выполнения которых меньше. Две другие линии построены с учетом того, что эти процессы имеют более высокий приоритет.

На рис. 9.13 показаны результаты того же анализа для низкоприоритетных длительных процессов. Как и следовало ожидать, у этих процессов при приоритетном планировании наблюдается снижение производительности.