Очередь со многими серверами
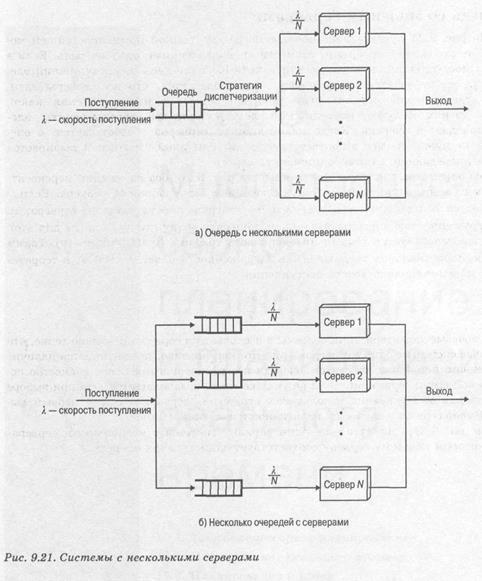
На рис. 9.21 представлено обобщение рассмотренной нами простейшей модели с несколькими серверами, совместно использующими одну очередь. Если в момент поступления элемента доступен хотя бы один сервер, поступивший элемент тут же передается этому серверу. Предполагается, что все серверы идентичны, так что если доступны несколько серверов, то не имеет значения, какой именно из них обслужит поступивший элемент. Если все серверы заняты, элемент попадает в очередь. Когда какой-либо из серверов освобождается, а очередь — не пуста, из нее в соответствии с той или иной стратегией выбирается элемент, передающийся освободившемуся серверу.
Все параметры системы, показанные на рис. 9.20, без изменений переносятся на многосерверную систему, за исключением загруженности сервера. Если у нас имеется N идентичных серверов и ρ— загруженность каждого сервера, то под загруженностью системы мы можем понимать величину Nρ; иногда для этой величины используется термин интенсивность трафика (traffic intensity). Таким образом, максимальная теоретическая загруженность равна N*l00%, а теоретическая максимальная скорость поступления
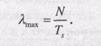
Ключевые характеристики системы с несколькими серверами обычно те же, что и в случае системы с одним сервером, так что, как правило, предполагается наличие бесконечного источника элементов, очереди неограниченного размера, совместно используемой всеми серверами. Если не указано иное, предполагается, что при выборе элемента для обслуживания используется стратегия "первым вошел — первым вышел". Выбор сервера в случае их идентичности значения не имеет.
На рис. 9.21,6 показан еще один вариант системы с несколькими серверами, в котором каждому серверу соответствует единственная очередь.
|
Дата добавления: 2016-06-05; просмотров: 1393;











