Выбор самого короткого процесса

Еще один путь к снижению перекоса в пользу длинных процессов — использование стратегии выбора самого короткого процесса (shortest process next — SPN). Это невытесняющая стратегия, при которой для выполнения выбирается процесс с наименьшим ожидаемым временем исполнения.

На рис. 9.5 и в табл. 9.5 приведены результаты применения данной стратегии к нашему примеру. Обратите внимание, что процесс Е обслуживается гораздо раньше, чем в случае применения FCFS-стратегии. В отношении времени отклика общая производительность системы также возрастает, но при этом увеличивается разброс его величины, в особенности для длинных процессов (и, соответственно, снижается предсказуемость).

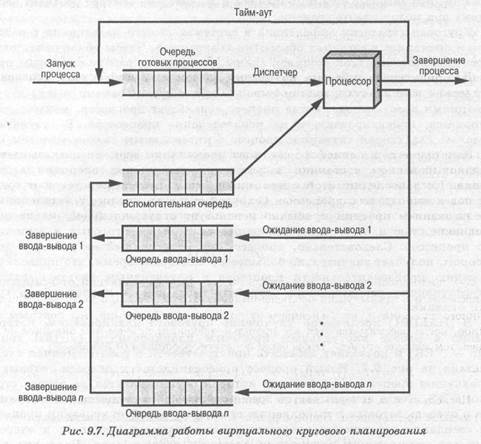
Основная трудность в применении стратегии SPN состоит в том, что для ее осуществления необходима по меньшей мере оценка времени выполнения, требующегося каждому процессу. При выполнении пакетных заданий может понадобиться оценка этого значения программистом и предоставление его операционной системе. Если оценка программиста существенно ниже реаль­ного времени выполнения, система может прекратить выполнение задания. В промышленных системах часто выполняются одни и те же задания, так что можно собрать достаточно точную статистику. В случае выполнения инте­рактивных процессов операционная система может поддерживать во время выполнения средний "разрыв" для каждого процесса. Простейшее вычисле­ние выглядит следующим образом:

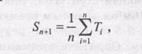(9.1)

где

T_i — время работы процессора для i-ro экземпляра данного процесса (общее время работы для пакетного задания, время разрыва при интерактивной работе);

S_t — предсказанное значение для i-гo экземпляра;

S₁ — предсказанное значение для первого экземпляра (не вычисляется).

Для того чтобы избежать повторного вычисления всей суммы, уравнение (9.1) можно записать следующим образом:

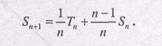(9.2)

Заметим, что в данной формуле все экземпляры при усреднении имеют одинаковый вес, хотя обычно следует дать больший вес экземплярам, выполнявшимся последними, так как они в большей степени отражают будущее поведение процесса. Обычная технология предсказания будущего значения на основе значений прошедших серий представляет собой взвешенное усреднение

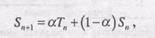(9.3)

где a— постоянный весовой множитель (0 < a < I), определяющий относительный вес последнего и предыдущих наблюдений (сравните с (9.2)). При использовании постоянного значения a, не зависящего от количества наблюдений, мы получаем ситуацию, когда рассматриваются все прошлые значения, причем чем значение более давнее, тем меньше его вес. Чтобы было понятнее, распишем (9.3) как

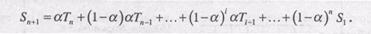(9.4)

Поскольку и a, и 1-a меньше единицы, каждый последующий множитель в (9.4) меньше предыдущего. Например, при a = 0.8 уравнение (9.4) записывается как

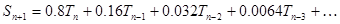
т.е. чем старее наблюдение, тем меньший вклад оно вносит в вычисляемое среднее значение.

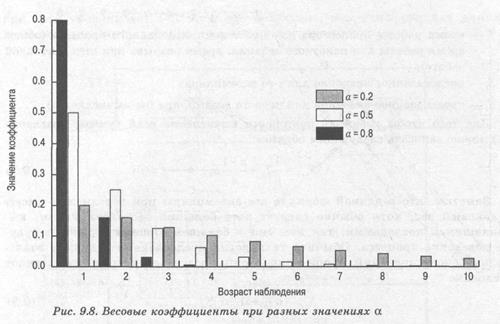
Значение коэффициента как функции от положения члена в сумме по­казано на рис. 9.8. Чем больше значение а, тем больший вес имеют последние наблюдения. При a = 0.8 в вычислении среднего значения, по сути, участвуют только три-четыре последних наблюдения, в то время как при a=0,2 заметный вклад вносят восьмое и более поздние наблюдения. Значения а, близкие к 1, позволяют нашему методу быстро реагировать на любые изменения, но при этом увеличивается и реакция на случайные отклонения от среднего значения при наблюдениях, что приводит к излишне резким изменениям вычисляемого значения.

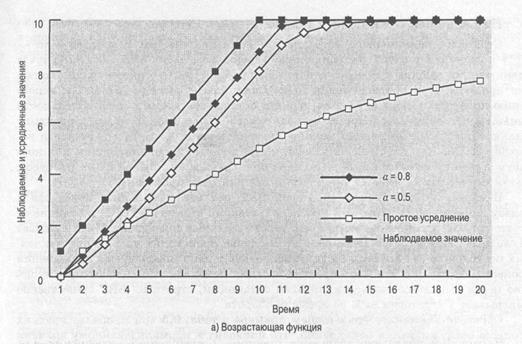
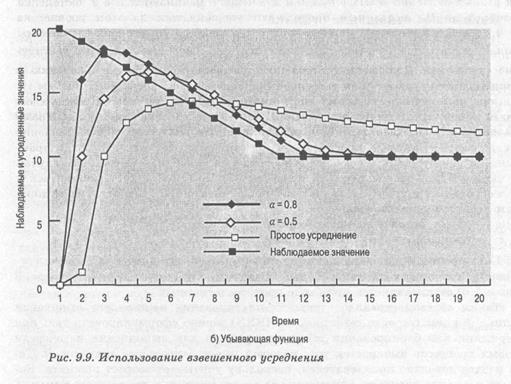
На рис. 9.9 приведено сравнение простого и взвешенного усреднения для двух разных значений а. На рис. 9.9,а значения aначинаются с 1 и постепенно вырастают до 10, после чего продолжают удерживаться на этом уровне; на рис. 9.9,6 наблюдаемые значения уменьшаются от 20 до 10. В обоих случаях мы начинаем с оценки S₁= 0. Обратите внимание на то, насколько быстрее реагирует на изменение наблюдаемых значений взвешенное среднее по сравнению с обычным средним, и чем больше значение a, тем выше скорость реакции.

Основной риск при использовании стратегии SPN заключается в возможном голодании длинных процессов при стабильной работе коротких процессов. Кроме того, хотя SPN снижает перекос в пользу длинных процессов, его применение нежелательно в системах с разделением времени или системах обработки транзакций из-за отсутствия вытеснения. Возвращаясь к анализу наихудшего случая для метода FCFS, мы увидим, что процессы W, X, Y и Z будут выполняться в том же порядке, причем обслуживание процесса Y имеет значительно худшие параметры, чем у других процессов.