Сканер с. 69 – 72 4 класс Истомина (страницы вставлены)
- Я согласна с тобой, но можно рассуждать проще. Когда мы делим на 10, то фактически узнаём, сколько в числе десятков, при делении на 100 — сколько в числе сотен, а при делении на 1000 — сколько в числе тысяч.
54 : 10 = 5 (ост. 4)
4125 : 100 = 41 (ост. 25)
251384 : 1000 =251 (ост. 384)
Выполни деление, рассуждая, как Миша или как Маша.
139)
| 8:7 | 7 :6 | 9 :8 | 12: 11 |
| 16 :7 | 14 :6 | 18 : 8 | 24 : И |
| 24 :7 | 21 :6 | 27:8 | 36: И |
| 32 :7 | 28 :6 | • • • | • • • |
По какому правилу составлены столбики выражений?
б) Выполни деление с остатком.
в) Какую закономерность ты заметил?
г) Продолжи записывать выражения в каждом
столбике по тому же правилу и выполни деление.
В каком выражении эта закономерность нарушится? Почему?
140. В книге 4 рассказа. Один рассказ занимает 17 страниц, другой — в 3 раза больше, третий — на 15 страниц больше, чем второй. Сколько страниц занимает четвёртый рассказ, если всего в книге 150 страниц?
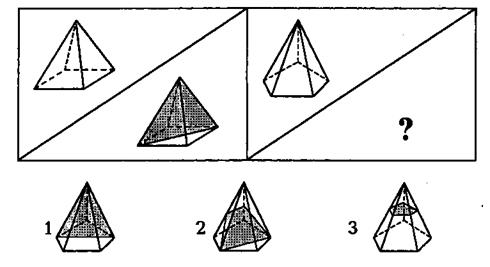
141. Выбери фигуру, которую нужно нарисовать.
|
142. В первый день в палатке продали 12 ящиков печенья, а во второй — 9 таких же ящиков. Сколько килограммов печенья продали в первый день, если всего его было 210 кг? Выбери схему, которая соответствует задаче, и запиши ее

|
решение по действиям.
70
143. Пекарня ежедневно выпекает одинаковое количество хлеба. Сколько хлеба выпекает пекарня за 9 дней, если за 3 дня она выпекает 510 кг?
144. В одном таксопарке 587 машин, в другом в 3 раза больше, а в третьем на 32 машины меньше, чем в первом. Сколько всего машин в трёх таксопарках?
Объясни, что обозначают выражения, записанные по условию задачи: 587 • 3 - 587; 587 • 3 - (587 - 32).
145. В двух хранилищах 99890 кг картофеля. Когда из каждого хранилища взяли картофеля поровну, то в первом осталось 32500 кг, а во втором 45390 кг.
Сколько картофеля было в каждом хранилище?
Нарисуй схему, она поможет тебе решить задачу.
146. В трёх ящиках 110 кг яблок. В первом на 35 кг больше, чем во втором, а во втором на 15 кг больше, чем в третьем. Сколько яблок в каждом ящике?
Нарисуй схему, она поможет тебе решить задачу.
147. За три дня выставку посетили 870 человек. В первый день 320 человек, во второй на 90 человек больше, чем в первый. Сколько человек посетило выставку в третий день?
148. Периметр прямоугольника 70 см, причём его длина на 15 см больше, чем ширина. Найди длину и ширину прямоугольника. Вычисли его площадь.
Выбери схему, которая соответствует условию задачи, и запиши её решение.
149. В то время как мама обрабатывает 17 кустов клубники, дочка успевает обработать 12 кустов, а бабушка — 10. Сколько кустов клубники они обработали все вместе, если бабушка обработала всего 80 кустов?
150. На ферме содержатся коровы, овцы, козы — всего 3320 животных. Коров на 120 меньше, чем овец, и на 100 больше, чем коз. Сколько на ферме коз?
Рассмотри схему, она поможет решить задачу.
|
Кор.
Ов. Коз.
Проведем методический анализ страниц 69 – 72, выбирая материал для построения урока решения задач:
1. Тема урока: Обучение решению задач.
2. Методическая цель урока: учить детей решать задачи, развивать анализ и синтез, моделирующую деятельность и вычислительную деятельность.
3. Анализ заданий на странице учебника: поскольку в данном учебнике нет принципа постраничного распределения материала для урока, выбираем для данного урока № 140 – 145.
Все эти задания (кроме 141) – задачи. Все задачи разного типа, поэтому их следует решать на уроке с подробным анализом решения.
Задание 141. Цель – развитие пространственного мышления, сравнения и выделения общих признаков пар объектов.
Главная дидактическая цель урока: обучающая и развивающая. Данный учебник содержит большое количество задач достаточно высокого уровня сложности. Решение с детьми таких задач при условии высокой доли их самостоятельности благотворно влияет на развитие математического мышления и формирование общего умения решать задачи.
Какие могут быть трудности и как их предупредить: трудности данного урока обусловлены объективной трудностью задач, содержащихся в уроке. Предупредить эти трудности учитель может, используя разнообразные методические приемы обучения решению задач. В данном уроке рекомендуется активное использование схематических рисунков в качестве моделей задач, помогающих детям в их решении.
Формы организации деятельности детей на уроке:фронтальная работа с элементами индивидуализации.
Наглядные материалы: рисунки схем на доске.
Приведем конспект урока по данным страницам:
Тема:Решение задач.
Цель урока:развивать умениерешать задачи с использованием схем.
Учитель сообщает, что сегодня на уроке дети будут решать различные задачи. Далее все тексты задач приводятся в данном пособии, поскольку не всегда учитель может обратиться за текстом задачи к учебнику, по которому он не работает.
Задача № 140:В книге 4 рассказа. Один рассказ занимает 17 страниц, другой – в 3 раза больше, третий – на 15 страниц больше, чем второй. Сколько страниц занимает четвертый рассказ, если всего в книге 150 страниц?
Методика работы над задачей.
Задача уже знакомой детям структуры (встречалась ранее см. № 9, 19, 27… этого учебника). Можно предложить детям самостоятельно составить к ней чертеж, а затем обсудить его, сверяя каждое данное с текстом задачи:
 I 17
I 17
II
III 15 150
IV
?
- Сравните первый и второй отрезки на чертеже. ( Второй в 3 раза длиннее, чем первый.)
- Сравните второй и третий отрезки. Учитель обводит левую часть третьего отрезка красным мелом, а правую - синим. Дети отмечают, что красный отрезок совпадает по длине со вторым отрезком.
- Если второй отрезок содержит 3 раза по 17, то что можно сказать о третьем отрезке? ( Он содержит 17 • 3 + 15 )
Учитель отмечает это на чертеже:

 17
17


 15 150
15 150

?
-Запишите выражением: как найти количество страниц в первых трех рассказах и найдите это число.
17 • 7 + 15 = 119 + 15 = 134 (с.)
- Можно ли теперь ответить на вопрос задачи? (Да. 150 – 134 = 16 с.)
Задача № 142:В первый день в палатке продали 12 ящиков печенья, а во второй — 9 таких же ящиков. Сколько килограммов печенья продали в первый день, если всего его было 210 кг?
В учебнике сказано: Выбери схему, которая соответствует задаче, и запиши ее решение по действиям.
 12 ящ. 12 ящ. 9 ящ.
12 ящ. 12 ящ. 9 ящ.

9 ящ. 210 кг
210 кг

 12 ящ. 9 ящ. 12 ящ. 9 ящ.
12 ящ. 9 ящ. 12 ящ. 9 ящ.
210 кг 210 кг
Методика работы над задачей.
Типовая задача на пропорциональное деление. В учебнике даны схемы. Задаче соответствуют две первые схемы, но на них не обозначен вопрос. Учитель предлагает объяснить, почему третья и четвертая схемы не подходят к задаче. (210 кг печень было всего – это общее количество, а не часть.)
Затем составляется план решения. Его можно составлять «от вопроса»:
- Прочитайте вопрос задачи. ( Сколько килограммов печенья продали в первый день?)
- Что нужно знать, чтобы ответить на вопрос задачи? ( Сколько продано ящиков и сколько килограммов в каждом ящике.)
- Как узнать, сколько килограммов в каждом ящике? (Разделить общую массу на количество ящиков.) Что мы знаем из этих данных? (Общую массу.)
- Как найти общее количество ящиков? ( 9 + 12 = 21 ящик)
- Запишите решение задачи по действиям.
Когда дети запишут решение задачи по действиям, учитель предлагает устно сформулировать пояснения к каждому действию:
1) 9 + 12 = 21 ( ящ. ) – всего ящиков
2) 210 : 21 = 10 ( кг) – в одном ящике
3) 10 • 12 = 120 ( кг) – продали в первый день
Анализируя последнее действие, учитель предлагает объяснить, как легче получить ответ: 10 • 12 = 12 • 10 = 120 . Повторяется правило умножения на 10.
В качестве дополнительной работы учитель предлагает подумать, на какой вопрос еще можно ответить в задаче? (Сколько кг печенья продали во 2 день? 10 • 9 = 90 или 210 – 120 = 90)
Затем, используя рис. 1 из учебника (нарисованный на доске), учитель рисует рядом такой вариант схемы:
 12 ящ.
12 ящ.
9 ящ. 30 кг ?
Учитель предлагает сравнить два рисунка и сформулировать задачу по новому рисунку. Задачи сравниваются: они взаимно-обратные. Составляется план решения новой задачи. Этот план можно составить «от данных»:
1. Узнаем, на сколько ящиков в первый день продали больше, чем во второй день?
2. Узнаем, сколько кг в одном ящике?
3. Узнаем, сколько всего ящиков продано?
4. Узнаем, сколько всего печенья продано?
Это план может быть записан на доске. Затем дети самостоятельно по плану записывают решение задачи.
Задача № 143:Пекарня ежедневно выпекает одинаковое количество хлеба. Сколько хлеба выпекает пекарня за 9 дней, если за 3 дня она выпекает 510 кг?
Нарисуй схему, она поможет тебе решить задачу.
Методика работы над задачей.
Задача на нахождение четвертого пропорционального. Если составлять к ней таблицу или краткую запись, то решать ее нужно будет в два действия
1) 510 : 3 = 170 кг 2) 170 • 9 = 1530 кг.
Иллюстрация задачи графическим рисунком позволит решить ее одним действием.
После чтения текста, учитель задает опорные вопросы для составления рисунка:
- Что дано в задаче? (За 3 дня выпекают 510 кг хлеба.)
- Обозначим это на рисунке.

510 кг
- Что спрашивается в задаче? (Сколько хлеба выпекает пекарня за 9 дней?) У нас есть отрезок, обозначающий выпечку за три дня, как его использовать для обозначения нужной величины? (Повторить его три раза.)
- Обозначим вопрос задачи на рисунке.

510 кг

?
- Сравните длины отрезков, обозначенных дугами, что можно сказать о них? ( Они равные. Второй отрезок в три раза больше первого.)
- Что обозначает первый отрезок? (Выпечку за три дня.)
- Что обозначает второй отрезок? (Выпечку за 9 дней.)
- Как найти выпечку за 9 дней? (510 • 3 = 1530 кг)
- На какой еще вопрос можно ответить по имеющимся данным? (Сколько хлеба выпекается за 1 день?)
510 : 3 = 170 (кг)
- Что нужно изменить в задаче, чтобы без выполнения этого действия ее нельзя было решить?
Это сложный аналитический вопрос, требующий понимания структуры пропорциональной связи между данными. Если количество дней не будет пропорционально, то задачу нужно будет решать обычным способом, т.е. приведением к единице. Хорошо, если дети увидят, что следует изменить данное в вопросе, т.е. вместо 9 дней взять 8 дней или 10 дней. В этом случае действие приведения к единице будет необходимо.
Задача № 144:В одном таксопарке 587 машин, в другом в 3 раза больше, а в третьем на 32 машины меньше, чем в первом. Сколько всего машин в трёх таксопарках? Объясни, что обозначают выражения, записанные по условию задачи:
587 • 3 – 587; 587 • 3 – (587 – 32);
Методика работы над задачей.
Задача знакомой, часто встречающейся в этом учебнике структуры, может быть предложена для самостоятельной работы. Выполнение задания «ответь на вопросы» не требует решения задачи. Можно после прочтения текста сразу попросить детей объяснить выражения. Для этого можно выписать на доску их конструкцию пошагово:
587 - ?
587 • 3 - ?
587 • 3 – 587 - ?
587 – 32 - ?
587 • 3 – (587 – 32) - ?
Дети дают пояснения, соотнося каждую запись с условием задачи. Учитель записывает эти пояснения рядом с выражениями:
587 – машин в 1 парке
587 • 3 – машин во 2 парке
587 • 3 – 587 – на столько машин во 2 парке больше, чем в 1 парке
587 – 32 - машин в 3 парке
587 • 3 – (587 – 32) – на столько во 2 парке больше машин, чем в 3 парке
Затем читается вопрос задачи и разбор проводится аналитически: Что нужно знать, чтобы ответить на вопрос задачи? (Количество машин во всех трех парках.)
Учитель предлагает найти на доске и подчеркнуть красным мелом нужные для ответа на вопрос компоненты. Дети отмечают их. Затем можно предложить самостоятельно записать выражение (на доске и в тетрадях):
587 + 587 • 3 + (587 – 32) =
Разумнее проанализировать это выражение с точки зрения его рационализации, чем сразу выполнять вычисления по действиям. Учитель обращает внимание детей на сумму 587 + 587 • 3 – ее можно заменить произведением 587 • 4, тогда выражение примет вид 587 • 4 + 587 – 32 в данном случае скобки можно опустить, поскольку на результат они не будут влиять (их можно было сразу не ставить вообще). Анализ этого выражения позволяет его дальнейшую рационализацию:
587 • 5 – 32 =
Далее результат можно вычислять столбиком, или применить прием рационального вычисления, если дети с ним знакомы (умножение на 5):
 587 • 5 = 587 •10 : 2 = 5870 : 2 = 2500 + 400 + 35 = 2935
587 • 5 = 587 •10 : 2 = 5870 : 2 = 2500 + 400 + 35 = 2935
5000 800 70
2935 – 32 = 2933 ( м. )
Ответ: 2933 машины в трех парках.
Задача № 145:В двух хранилищах 99890 кг картофеля. Когда из каждого хранилища взяли картофеля поровну, то в первом осталось 32500 кг, а во втором 45390 кг. Сколько картофеля было в каждом хранилище?
Нарисуй схему, она поможет тебе решить задачу.
Методика работы над задачей.
Задача такой структуры впервые встречается в этом учебнике. В связи с этим ее можно считать центральной в данном уроке и на данной странице.

 В средней школе задачи такой структуры часто встречаются в пятом классе. Ее удобно решать с помощью уравнения, обозначив через х взятое количество картофеля, что сразу приводит к уравнению:
В средней школе задачи такой структуры часто встречаются в пятом классе. Ее удобно решать с помощью уравнения, обозначив через х взятое количество картофеля, что сразу приводит к уравнению:
32500 + х + 45390 + х = 99890
было в 1 сначала было во 2 сначала
Уравнение простой структуры, легко решается даже в 4 классе. Но в данном учебнике использование уравнений при решении задач на данном этапе не предусматривается.
Составление схемы к задаче требует аналитического подхода к разбору текста (от вопроса). Поскольку данные в задаче очень громоздкие, то первое прочтение текста обычно не приводит к осмыслению сути задачи. Следует просто убедиться в том, что у детей зафиксировался сюжет: Сколько было хранилищ? (2) Что сказано о количестве взятого из них картофеля? (Взяли поровну.) Что еще известно? ( Сколько было картофеля сначала и сколько осталось картофеля в каждом хранилище.)
- Обозначим количество картофеля в каждом хранилище произвольным отрезком:
 I
I
 II
II
- Как вы думаете, почему я рисую второй отрезок длиннее первого? Есть ли для этого основания, или я делаю это случайно?
- Попробуйте найти эти основания в тексте задачи. Если дети не могут сделать это самостоятельно, учитель прямо предлагает сравнить количества остатков картофеля в каждом хранилище. (Второй остаток больше.) А брали картофель как? (Поровну.) Если во 2 хранилище при этом больше осталось, то что это значит? (Что там и сначала было больше.)
 - Обозначьте на рисунке первое данное:
- Обозначьте на рисунке первое данное:
I 99890 кг
II
- Теперь нужно отметить на рисунке взятое из каждого хранилища равное количество картофеля и остаток. Как вы думаете, где удобнее для глаз отмечать отрезки, соответствующие взятому количеству картофеля? Если дети расходятся во мнениях, следует нарисовать на доске два рисунка, чтобы дети визуально оценили, какой из них удобнее для организации решения:
взяли осталось
 I 32500 кг
I 32500 кг
II осталось 99890 кг
Взяли 45390 кг
 32500 кг взяли
32500 кг взяли
I осталось взяли 99980 кг
II
осталось 45390 кг
Сравнение рисунков показывает, что на втором рисунке не так хорошо видно равенство взятых количеств, как первом. Далее учитель использует такой прием: закрывает часть рисунка листом бумаги, чтобы акцентировать его характерные особенности.
- Если бы не было этой части рисунка, как можно было бы найти взятое из каждого хранилища количество картофеля? (Общее количество разделить пополам.)
 взяли осталось
взяли осталось
I 32500 кг
II осталось 99890 кг
Взяли 45390 кг
- Можно ли это сделать в данной задаче? (Нет.) Почему? ( Есть два остатка 32500 кг и 45390 кг)
- Что можно узнать из этих данных? (Весь остаток.)
32 500 + 45 390 = 77 890 ( кг) – весь остаток
Учитель снова закрывает ту же часто чертежа, но на листе бумаги пишет маркером это число: 77 890 кг.
- Какие данные теперь есть? (Общее количество картофеля и весь остаток.)
- Что можно найти? (Весь взятый картофель.)
- Как найти?
99 890 – 77 890 = 22 000 (кг) – весь взятый картофель
- Что можно узнать, зная количество всего взятого картофеля? (Количество картофеля, взятого из одного хранилища.)
-Почему это можно найти? (Потому, что брали поровну, значит надо весь взятый картофель разделить пополам.)
22 000 : 2 = 11 000 (кг)
- Прочитайте вопрос задачи. Можем мы теперь на него ответить? (Да.)
32 500 + 11 000 = 43 500 (кг)
45 390 + 11 000 = 56 390 (кг)
- Как вы думаете, если бы брали не одинаковое количество, смогли бы мы решить задачу? (Нет.)
- Почему? (Мы не смогли бы найти взятое из каждого хранилища количество картофеля путем деления пополам.)
Примечание: далее задач такой структуры не встречается, поэтому имеет смысл предложить детям на следующем уроке задачу того же типа для самостоятельного решения и сравнения их структур. Например: На двух полках библиотеки 218 книг. Когда с каждой из них взяли равное количество книг, то на 1 полке осталось 42 книги, а на 2 полке – 116 книг. Сколько книг было на каждой полке сначала?
Для домашней работы может быть рекомендован № 141 и задача 573.
Урок 2.
Тема:Решение задач.
Цель:та же, что и в предыдущем уроке.
Урок можно начать с рекомендованной выше задачи. Затем перейти к задачам учебника.
Задача № 146:В трёх ящиках 110 кг яблок. В первом на 35 кг больше, чем во втором, а во втором на 15 кг больше, чем в третьем. Сколько яблок в каждом ящике?
Методика работы над задачей.
Большое количество разнообразных данных и соотношений между ними требует руководства анализом текста. Дети читают задачу самостоятельно («про себя»). Учитель задает вопросы для ориентировки в условии:
- Сколько было ящиков? (3) Что лежало в ящиках? (Яблоки.) Были ли ящики равны по массе? (Нет.) Что надо узнать? (Сколько яблок в каждом ящике.)
Затем к доске вызывается ребенок, и дальнейший анализ текста сопровождается составлением схемы:
- Обозначим каждый ящик отрезком. Рисуй первый отрезок:
I
- Прочитайте, что сказано о массе второго ящика (В 1 ящике на 35 кг больше, чем во втором.)
- Какой ящик тяжелее: 1 или 2? (Первый, на 35 кг.)
 -Какой отрезок будет короче? (Тот, что соответствует второму ящику, т.к. он легче на 35 кг.)
-Какой отрезок будет короче? (Тот, что соответствует второму ящику, т.к. он легче на 35 кг.)

 I35 кг
I35 кг
II
- Что сказано о соотношении масс 2 и 3 ящика? (Во 2 ящике на 15 кг больше, чем в 3 ящике.)
- Какой ящик тяжелее, 2 или 3 ? (Второй, на 15 кг.)
- Какой отрезок длиннее 2 или 3? (Второй.)
- Рисуем 3 отрезок короче второго и обозначаем разницу 15 кг:
I 35 кг

II 15 кг
III
- Что еще известно в задаче, но не обозначено на чертеже? (110 кг – общая масса.)
-Обозначим ее.
 I 35 кг
I 35 кг
II 15 кг 110 кг
III
 Далее учитель может использовать такой прием: он прочерчивает на рисунке дополнительную вертикальную линию и предлагает детям подумать, с какой целью он это сделал:
Далее учитель может использовать такой прием: он прочерчивает на рисунке дополнительную вертикальную линию и предлагает детям подумать, с какой целью он это сделал:
I 35 кг
II 15 кг 110 кг
III
Если дети не видят равных отрезков, то, используя две указки (прикладывая их к вертикалям), учитель выделяет эти отрезки на чертеже: что можно сказать о длинах этих отрезков? (Они равны.)
- Что обозначают эти отрезки? ( Массу яблок.)
- Что означают равные длины отрезков на рисунке? (Они означают равные массы.)
Используя цветной мел, дети обозначают равные отрезки, и подписывают соответствующие им массы.
 I 15 кг 35 кг
I 15 кг 35 кг
II 15 кг 110 кг
III
- Далее может быть использован тот же прием закрывания части чертежа, что и в предыдущей задаче. Учитель закрывает все известные отрезки, и спрашивает детей о длине трех оставшихся незакрытыми. (Они раны. Если бы не было второй части чертежа, то общую массу можно было бы разделить на 3.)
Затем учитель закрывает левую часть чертежа (неизвестные длины) и предлагает ответить на вопрос: что можно найти, зная все обозначенные длины. (Это - те числа, из-за которых массы ящиков не равны. Можно найти их сумму: 15 • 2 + 35 = 65 кг)
На листе бумаги, которым закрывается правая часть чертежа, записывается маркером это число.
- Что можно найти, зная всю разницу и всю массу яблок? (Сколько яблок приходится на 3 неизвестных отрезка.)
110 – 65 = 45 (кг)
- Какие эти три неизвестных отрезка по длине? (Равные.)
- Что теперь можно найти? (Массу яблок, приходящуюся на один неизвестный отрезок, который совпадает с массой третьего ящика.)
45 : 3 = 15 (кг)
- Что это число обозначает? (Массу яблок в 3 ящике.)
- Можно теперь найти массу яблок в остальных ящиках? (Да.)
- Закончите решение задачи самостоятельно.
Учитель дает время на запись действий, а затем дети комментируют свои записи.
15 + 15 = 30 (кг) – во 2 ящике
30 + 35 = 65 (кг) – в 1 ящике
-Как проверить ответ задачи? (Сложить все полученные числа.)
15 + 30 + 65 = 110 (кг) – значит, задача решена верно.
Задача № 147:За три дня выставку посетили 870 человек. В первый день 320 человек, во второй на 90 человек больше, чем в первый. Сколько человек посетило выставку в третий день?
Методика работы над задачей.
Задача аналогичной структуры, что и №146. Работа над ней может быть в значительной мере самостоятельно. Учитель предлагает детям сделать чертеж в тетрадях. Проходя по классу, отмечает для себя, кто из детей не справился с работой. Затем можно вынести на доску ошибочный вариант (учитель рисует его сам, чтобы не акцентировать ошибки детей).
- Я рисую чертеж с ошибкой. Найдите ее.
Если все дети справились с рисунком, он анализируется и составляется план решения:
 I 320 ч.
I 320 ч.
II 90 ч. 870 ч.
III
?
- Что можно найти первым действием? (Количество посетителей во 2 день.) 320 + 90 = 410 (ч.)
- Что можно найти вторым действием? (Количество посетителей в два первых дня.) 410 + 320 = 730 (ч.)
- Что можно найти третьим действием? (Количество посетителей в третий день.) 870 – 730 = 140 (ч.)
После записи ответа можно сравнить числа количества посетителей за три дня, записать их по возрастанию: 140 410 320
- В какой день было больше всего посетителей? Меньше всего? Чем похожи все числа? (Целые десятки.)
- Посмотрите внимательно на эти три числа и подумайте, чем они еще похожи? (Сумма цифр каждого равна 5.)
- На какие числа разделятся все три числа без остатка? ( На 10, на 5 и на 2.)
- Разделятся ли они на 3? На 9? (Нет.)
Здесь можно предложить вспомнить признаки делимости на 3 и на 9 (Сумма цифр числа должна делиться на 3 и на 9 соответственно.)
Можно обсудить делимость этих чисел на 6. (Если не делятся на 3, то и на 6 не разделятся, т.к. для делимости на 6 нужна одновременная делимость на 3 и на 2.)
Можно познакомить детей с признаком делимости на 4: если две последние цифры числа образуют число, делящееся на 4, то и все число делится на 4. Следовательно, 140 и 320 разделятся на 4, а 410 не разделится без остатка. Дети по рядам выполняют проверку этих делений (три ученика у доски) и убеждаются в том, это именно так.
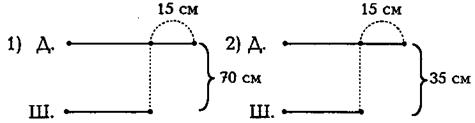
Задача № 148:Периметр прямоугольника 70 см, причем его длина на 15 см больше, чем ширина. Найди длину и ширину прямоугольника. Вычисли его площадь.
В учебнике дана рекомендация:
Выбери схему, которая соответствует условию задачи, и запиши ее решение.
 1) 15 см 2) 15 см
1) 15 см 2) 15 см
 Д. Д.
Д. Д.
Ш. 70 см Ш. 35 см
Методика работы над задачей.
В учебнике предлагается выбор одной из двух данных схем, но нагляднее эта задача выглядит на рабочем рисунке привычной формы. Поэтому, прежде чем предлагать детям выбор схемы, удобно сделать на доске рабочий рисунок. Иначе дети могут выбрать 1 схему, а не вторую, поскольку число 70 есть в условии, а числа 35 – нет в условии.
 После чтения текста, учитель предлагает обозначить на рисунке все данные: Д.
После чтения текста, учитель предлагает обозначить на рисунке все данные: Д.
Ш. Ш.
Ш. 15 см
Д.
Р = д + д + ш + ш = 70 см
Р = ( д + ш ) • 2 = 70 см, тогда
д + ш = 35 см
После получения этого вывода можно адресовать детей к учебнику с целью выбора подходящей схемы и записи решения.
Можно пойти и другим путем. Поскольку на рисунке уже обозначено, что д = ш + 15, то можно составить символическую формулу:
д + ш = ш + 15 + ш = 35 см, тогда
2 ш + 15 = 35 см, значит
2 ш = 20 см
ш = 10 см, тогда
д = 10 + 15 = 25 см
Использование рабочего рисунка подсказывает еще один способ решения задачи, который учитель может предложить поискать детям. Этот способ не короче, но остроумнее и использует не только свойство прямоугольника, но и свойство квадрата. Чтобы подтолкнуть детей к этому способу, учитель делает дополнительные построения:
 Д 15
Д 15

Ш Ш

 Ш
Ш
Д
- Что представляет собой заштрихованная фигура? (Квадрат с длиной стороны, равной ширине прямоугольника.)
- Чему равен его периметр? ( 4 ш)
- Можно ли написать, что 4ш = 70 см? (Нет, 70 см - это периметр прямоугольника, а не квадрата.)
(ш + д) • 2 = 70 см – по условию
Затем учитель обращает внимание детей на разницу в 15 см, обводя оба отрезка красным мелом. Дети замечают, что разницу можно учесть
15 • 2 = 30 см
70 – 30 = 40 см – это число соответствует периметру квадрата
4 ш = 40 см, значит ш = 10 см, д = 25 см.
В качестве работы над задачей после ее решения, учитель предлагает подумать, может ли периметр квадрата выражаться числом 70? Здесь можно вспомнить признак делимости на 4. Число, не делящееся на 4 без остатка, не может выражать периметр квадрата (в начальной школе дети работают только в области натуральных чисел, поэтому речь идет о делимости нацело).
- Может ли нечетное число выражать периметр прямоугольника? (Нет, т.к. левая часть равенства 2 • ( а + b) = Р делится на 2, значит и правая часть должна делиться на 2).
Задача № 149:В то время как мама обрабатывает 17 кустов клубники, дочка успевает обработать 12 кустов, а бабушка – 10. Сколько кустов клубники они обработали все вместе, если бабушка обработала всего 80 кустов?
Методика работы над задачей.
Задача составная, содержит три простые задачи: на кратное сравнение, на нахождение суммы и на смысл умножения. Текст задачи можно считать трансформированным, поскольку одно данное (80 кустов) содержится в вопросе.
Перед решением данной задачи, в качестве подготовительной можно предложить такую задачу:
Брат и сестра моют тарелки: пока брат моет 4 тарелки, сестра успевает вымыть 6 тарелок. Сколько тарелок они вымыли, если сестра помыла 18 тарелок?
 Для решения этой задачи учитель предлагает построить вещественную модель, используя счетные палочки. Для работы на фланелеграфе можно использовать полоски бархатной бумаги, изображающие палочки. Один ученик строит модель задачи на фланелеграфе, остальные – на столах, используя палочки.
Для решения этой задачи учитель предлагает построить вещественную модель, используя счетные палочки. Для работы на фланелеграфе можно использовать полоски бархатной бумаги, изображающие палочки. Один ученик строит модель задачи на фланелеграфе, остальные – на столах, используя палочки.
Брат
Сестра
Анализ модели показывает способ решения: 18 тарелок можно распределить на три группы по 6 тарелок, значит, брат вымыл три группы по 4 тарелки, т.е. 12 тарелок. Общее количество – 30 тарелок.
Другой способ: Можно найти число тарелок в одной группе 4 + 6 = 10т., а затем повторить это количество трижды.
Решение этой задачи подсказывает способ решения задачи 149.
Учитель может предложить нарисовать модель группы, используя отрезки:
 Мать 17 к.
Мать 17 к.
Дочь 12 к. группа 10+12 + 17 = 39 (к.)
Бабушка 10 к.
Затем проводится анализ второй половины текста:
- Какое данное мы еще не использовали при решении задачи? (Всего 80 кустов обработала бабушка.)
- Мы выделили удобную для дальнейших подсчетов группу и обозначили ее в рисунке. Какое количество кустов в этой группе обрабатывает бабушка? (10 кустов)
- Как определить, сколько таких групп мы должны учесть, при ответе на вопрос задачи? (80 : 10 = 8 групп)
- Сколько раз нужно будет повторить группу из 39 кустов? (8 раз)
- Найдите ответ задачи.
39 • 8 = 312 (кустов)
В качестве дополнительного задания, можно предложить детям подумать, как быстро («в уме») подсчитать это произведение:
40 • 8 – 8 = 312
Поскольку данная задача предварялась подготовительной задачей, вся работа над ней занимает не менее 15 минут, поэтому дополнительная работа над задачей после ее решения не нужна. Полезно предложить детям самим составить подобную задачу на другую тему, это поможет зафиксировать в памяти данный тип задач, встречаемый достаточно редко.
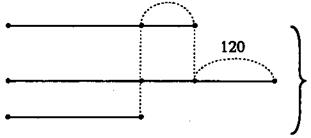
Задача № 150:На ферме содержатся коровы, овцы, козы – всего 3320 животных. Коров на 120 меньше, чем овец, и на 100 больше, чем коз. Сколько на ферме коз?
В учебнике дана схема и рекомендация:
Рассмотри схему, она поможет решить задачу.
 Кор.
Кор.
Ов. 120 3320
 Коз.
Коз.
Методика работы над задачей.
Задача уже не раз встречавшейся структуры ( ее можно задать и для домашней работы, предварительно разобрав). Учитель может предложить детям самостоятельно использовать на готовой схеме прием закрывания части чертежа полоской бумаги или рукой.
- Закройте пальцами правую часть чертежа. Что можно сказать о длинах трех отрезков, оставшихся незакрытыми? ( Они равны.)
- Закройте теперь левой рукой эти три равных отрезка. Что можно сказать о длинах незакрытых отрезков? Известны они? (Да, известны.)
- Можно ли найти их сумму? (Да.)
100 + 100 + 120 = 320 (ж.)
- Что можно найти теперь, зная разницу 320 и общую сумму 3320? (Сумму трех равных отрезков.)
3320 – 320 = 3000 (ж.)
- Что означает это число? (Число коз.)
- Найдите самостоятельно число коров и овец.
Дети выполняют действия и комментируют свои записи. Затем выполняют проверку, складывая все полученные числа.
1000 + 100 = 1100 (ж.) – коров
1000 + 100 + 120 = 1220 (ж.) – овец
1220 + 1000 + 1100 = 3320 (ж.) – всего животных
Можно выписать все числа ответов по возрастанию: 1000, 1100, 1220 и провести с ними работу, как в задаче 147, повторяя признаки делимости чисел.
***
Как видно из приводимых конспектов уроков, планирование урока – это в значительной мере творческий процесс. В принципе, приводимые уроки можно проводить при работе по любому учебнику, заменяя работу с учебником М.И. Моро на работу с тем учебником, по которому учитель работает. Суть в том, что эти уроки ориентированы на математическую суть программного материала, а не на содержание учебника, а математическая суть всех учебников едина (как показывает анализ, приведенный в главе 2). Но в то же время они показывают, что упреки учителей к традиционным учебникам в целом необоснованны, поскольку учебник – это лишь «канва» урока, и только от самого учителя зависит, что составляет его «тело», т.е. его внутреннее наполнение.
Приводя эти конспекты, мы хотели показать, что методическая фантазия учителя плюс хорошее владение содержанием и знание психологических особенностей процесса обучения младших школьников определяет качество урока математики. В конце концов, никто не запрещает учителю листать страницы этого учебника как ему удобно, и никто не запрещает ему вовсе не открывать учебник на уроке, если он не считает, что учебник на этом уроке будет необходим. Конечно, прекрасно, если учебник полностью соответствует желаниям и методическим потребностям учителя, но как показывает практика реализации альтернативных учебников по математике для начальной школы, количество которых сегодня подходит к двум десяткам, это разнообразие вовсе не облегчает жизнь учителя. И сегодня, как двадцать лет назад, учитель часто недоволен учебником, который кажется ему недостаточно разработанным, хотя двадцать лет назад у нас у всех был только один учебник, а сегодня их – множество, и новые продолжают появляться почти ежегодно. Но не всех это радует, поскольку авторы пишут учебники, не снабжая их методическими разработками уроков, а такая ситуация неминуемо требует от учителя собственной активной методической деятельности по анализу содержания учебников и соотнесению его с программой, проведения методического анализа каждой страницы учебника и активного методического творчества при разработке уроков.
Именно эту мысль подтверждают последние в данном параграфе разработки уроков по учебнику Н.Б. Истоминой, где уроки решения задач следует проводить систематически. На таком уроке учитель полностью сосредоточивает учебный процесс на решении целого комплекта непростых задач на одном уроке. Для того чтобы такой урок не превращался в мучение для учителя и непосильную проблему для детей, необходима тщательная методическая разработка каждой задачи, использование разнообразных приемов помощи детям, подведения их к пониманию способа решения той или иной задачи. Приведенные конспекты очевидно показывают, что методическая работа учителя над каждой задачей этого учебника является необходимым условием для организации деятельности детей на уроке. Эти задачи нельзя решать по шаблону, поскольку они нешаблонны. Практически все задачи – нетиповые, поэтому их нельзя «отработать»: каждая новая задача – это новая проблема как для учителя, так и для ребенка. Однако процесс преодоления этой проблемы как раз и является тем процессом, который обеспечивает обучение на высоком уровне трудности, являющееся очень сильным способом развития математического мышления учащихся.
Дата добавления: 2021-12-14; просмотров: 597;











