Кинематическое исследование механизмов

Целью кинематического исследования механики является определение положения звеньев в механизме, траектории определенных точек, определение скоростей звеньев и скоростей отдельных точек механизма, определение ускорений отдельных точек механизма.

Кинематическое исследование в механике может выполняться аналитическим методом, графическим методом и графоаналитическим способом.

Аналитический метод. Этот метод заключается в использование аналитических соотношений, связывающих кинематические параметры ведущего звена и ведомых звеньев, с помощью метрических характеристик.

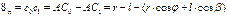
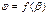
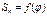
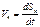
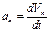
Графический метод (метод кинематической диаграммы)

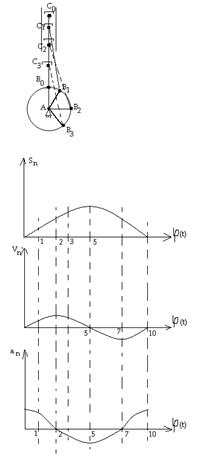
План скоростей механизма и его свойства

Для выполнения кинематического исследования любым методом должны быть заданы размеры звеньев и закон движения ведущего звена.

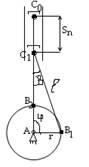
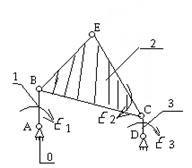
1) Вычерчивается план механизма (кинематическая схема) для исследуемого положения в масштабе 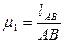, где l_AB – фактическая, натуральная дина; АВ – изображение звена на плане механизма

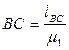
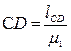
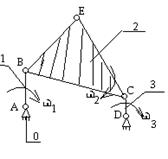
2) Определяем скорость точки В: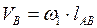

3)Записываем векторные уравнения для определения скорости т. С

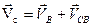
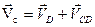
4)Для решения векторного уравнения графическим методом построим план скоростей в масштабе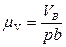

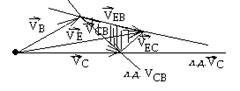
5) Определяем значение скоростей из построенного плана

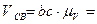
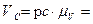
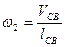
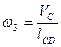
6) Записываем векторные уравнения для определения скорости т. Е и аналогично решаем

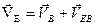
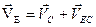
Свойства плана скоростей

1) Вектор, выходящий из полюса плана скоростей, представляет собой абсолютную скорость точек звеньев механизма (V_B; V_Е; V_С)

2) Векторы, соединяющие на плане скоростей концы векторов абсолютных скоростей, представляют собой относительные скорости (V_CB; V_EB)

3) Теорема подобия. Концы векторов абсолютных скоростей точек механизма, жёстко связанных между собой или принадлежащих одному звену, образуют подобиные фигуры, сходственно расположенные и повёрнутые на 90 в сторону вращения звена, относительно фигур, образованных этими же точками на плане механизма.

План ускорений механизма и его свойства

Для выполнения кинематического исследования любым методом должны быть заданы размеры звеньев и закон движения ведущего звена.

1) Вычерчивается план механизма (кинематическая схема) для исследуемого положения в масштабе 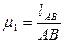, где l_AB – фактическая, натуральная дина; АВ – изображение звена на плане механизма

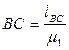
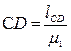
2) Определяем ускорение точки В: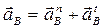

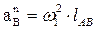
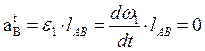, т.к.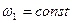

3)Записываем векторные уравнения для определения ускорения т. С

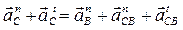
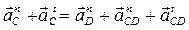
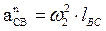
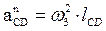
4)Для решения векторного уравнения графическим методом построим план ускорений в масштабе 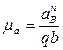. Определяем отрезки для построения известных ускорений на плане:

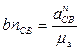
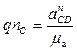
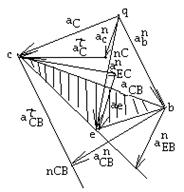
5) Определяем значение ускорений из построенного плана

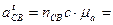
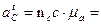
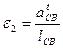
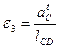
6) Записываем векторные уравнения для определения ускорения т. Е и аналогично решаем

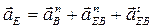
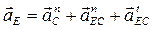
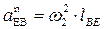
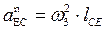
Свойства плана ускорений:

1) Вектор, выходящий из полюса плана ускорений, представляет собой абсолютное ускорение точек звеньев механизма (а_B; а_Е; а_С)

2) Отрезки, соединяющие на плане ускорений концы абсолютных ускорений, представляют собой полное относительное ускорение (a_CB; a_EB; a_EC)

3) Теорема подобия. Концы векторов абсолютных ускорений точек звеньев механизма, жёстко связанных между собой или принадлежащих одному звену, на плане ускорений изображают подобиные фигуры, сходственно расположенные и повёрнутые на угол (180-α), 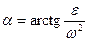, относительно фигур, образованных этими же точками на плане механизма.

Без использования угла α подобные фигуры можно построить с использованием правила обхода точек, которое должно быть одинаково на плане механизма и плане ускорений.