Пример создания модели
Создать модель движения системы (торпеды) в горизонтальном канале, состоящую из подмодели углового движения вокруг вертикальной оси и из подмодели цепи управления.
При этом подмодель углового движения может быть представлена в виде двух последовательно соединенных звеньев:
- апериодического
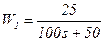 и – интегрирующего
и – интегрирующего 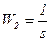 .
.
В свою очередь подмодель цепи управления может быть представлена в виде двух параллельно соединенных частей:
– части, управляемой гироскопом направления и представляющей собой обычное усилительное звено K;
- части, управляемой гиротахометром, которую можно представить как дифференцирующе-колебательное звено W3.
 Соответствующая структурная схема имеет вид, представленный на рисунке,
Соответствующая структурная схема имеет вид, представленный на рисунке,
где M – момент внешних сил относительно вертикали;
ω- угловая скорость торпеды;
ψ – угол поворота торпеды вокруг вертикали (угол рыскания).
Mу – момент управляющих сил, создаваемый при помощи рулей управления.
Решение.
Подмодель углового движения:
>> W1=tf(25,[100 50])
Transfer function:
---------------
100 s + 50
>> W2=tf(1, [1 0])
Transfer function:
---.
s
Последовательное соединение этих звеньев можно осуществить двумя способами:
– применением процедуры series:
>> W0=series(W1, W2)
Transfer function:
---------------------;
100 s^2 + 50 s
- либо просто операцией “перемножения” моделей:
>> W01=W1*W2
Transfer function:
----------------------.
100 s^2 + 50 s
Теперь сформируем цепь управления, входом которой является угол рыскания торпеды ψ, а выходом – момент Mу, накладываемый на торпеду со стороны ее рулей направления.
Усилительное звено:
>> K=tf(2,1)
Transfer function:
Дифференцирующе-колебательное звено W3:
>> W3=tf([100 0], [1 10 100])
Transfer function:
100 s
-----------------------.
s^2 + 10 s + 100
Параллельное соединение этих двух звеньев управления можно осуществить тоже двумя способами:
- либо используя процедуру parallel
>> U1=parallel(K,W3)
Transfer function:
2 s^2 + 120 s + 200
-------------------
s^2 + 10 s + 100
- либо применяя операцию “сложения” моделей
>> U=K+W3
Transfer function:
2 s^2 + 120 s + 200
------------------------.
s^2 + 10 s + 100
Теперь найдем модель всей САУ угловым движением торпеды, рассматривая цепь управления как цепь отрицательной обратной связи для торпеды, пользуясь для объединения прямой и обратной цепи процедурой feedback:
>> sys=feedback(W01,U)
Transfer function:
25 s^2 + 250 s + 2500
-------------------------------------------------------------------.
100 s^4 + 1050 s^3 + 10550 s^2 + 8000 s + 5000
После того, как система сформирована, можно ввести при помощи процедуры setнекоторые ее символьные описания. В частности присвоить названия входам и выходам системы, а также дать краткий комментарий к самой системе.
>> set(sys,'InputName','Момент сил', 'OutputName','Угол рыскания')
>> set(sys,'Notes','Угловое движение торпеды')
>> get(sys)
num: {[0 0 25 250 2.5e+003]}
den: {[100 1.05e+003 1.06e+004 8e+003 5e+003]}
Variable: 's'
Ts: 0
ioDelay: 0
InputDelay: 0
OutputDelay: 0
InputName: {'Момент сил'}
OutputName: {'Угол рыскания'}
InputGroup: [1x1 struct]
OutputGroup: [1x1 struct]
Notes: {'Угловое движение торпеды'}
UserData: []
9.3.3. Анализ системы
Пакет CONTROL предоставляет пакет процедур для осуществления анализа САУ, прежде всего, для определения отклика системы на внешние воздействия как во временной, так и в частотной областях.
Для нахождения временныхоткликов системы на внешние воздействия некоторых видов предусмотрены функции:
impulseНахождение отклика на импульсное входное воздействие.
stepНахождение реакции системы на единичный скачок входного воздействия.
initialОпределение собственного движения системы при произвольных начальных условиях.
lsimОпределение реакции системы на входное воздействие произвольной формы, задаваемое в виде вектора его значений во времени.
Группа процедур для представления реакции системы на гармонические воздействия в частотнойобласти:
bodeСтроит график АЧХ и ФЧХ (диаграмму Боде) указанной системы.
nyquistСтроит в комплексной плоскости график АФХ разомкнутой системы в полярных декартовых координатах.
nicholsСтроит карту Николса системы, т.е. график АФХ разомкнутой системы в декартовых координатах.
sigmaСтроит график зависимости от частоты сингулярных значений системы; обычно совпадает с АЧХ системы.
marginСтроит диаграмму Боде с указанием запасов по амплитуде и по фазе.
Процедуры, вычисляющие отдельные характеристики и графически показывающие расположение полюсов и нулей системы.
poleРасчет полюсов системы.
zpkdataРасчет полюсов, нулей и коэффициента передачи системы.
pzmapПостроение на комплексной плоскости карты расположения нулей и полюсов системы.
Примеры анализа во временной области
 1. Применяя процедуру step к созданной выше модели,
1. Применяя процедуру step к созданной выше модели,
>> step(sys)
можно получить график
2. Аналогично, использование процедуры impulse
>> impulse(sys)
приведет к появлению в графическом окне графика, приведенного ниже:

3. При применении процедуры initialнеобходимо в число входных параметров включить, во-первых, полный вектор всех начальных условий по переменным состояния, а, во-вторых, момент времени окончания процесса интегрирования.
>> sssys=ss(sys)
>> initial(sssys,[0 0 0 1],20)
Получим
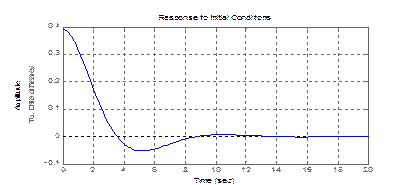
 4. Для применения процедуры lsimнеобходимо предварительно задать вектор t значений времени, в которых будут заданы значения входного воздействия, а затем задать вектор u значений входной величины в указанные моменты времени
4. Для применения процедуры lsimнеобходимо предварительно задать вектор t значений времени, в которых будут заданы значения входного воздействия, а затем задать вектор u значений входной величины в указанные моменты времени
>> t=0:0.01:40; u=sin(t); lsim(sssys,u,t);grid
 Результат представлен на следующей фигуре:
Результат представлен на следующей фигуре:
Примеры анализа в частотной области
1.>> bode(sys)
2.>> nyquist(sys)
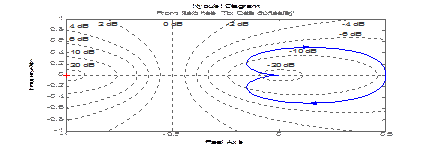
3.>> nichols(sys)
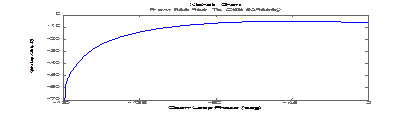
4.>> sigma(sys)
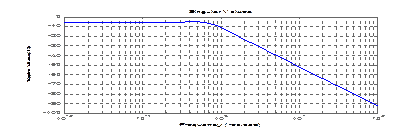
5.>> margin(sys);grid
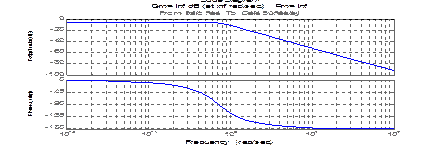
Примеры применения процедур для вычисления полюсов и нулей системы.
1.>> pole(sys)
ans =
-4.8653 + 8.5924i
-4.8653 - 8.5924i
-0.3847 + 0.6040i
-0.3847 - 0.6040i
2.>> sysz=zpk(sys)
Zero/pole/gain from input "Момент сил" to output "Угол рыскания":
0.25 (s^2 + 10s + 100)
------------------------------------------------
(s^2 + 0.7693s + 0.5128) (s^2 + 9.731s + 97.5)
3.>> [z,p,k]=zpkdata(sysz,'v')
z =
-5.0000 + 8.6603i
-5.0000 - 8.6603i
p =
-4.8653 + 8.5924i
-4.8653 - 8.5924i
-0.3847 + 0.6040i
-0.3847 - 0.6040i
k =
0.2500
4.>> pzmap(sys); grid
Результат представлен на рисунке ниже
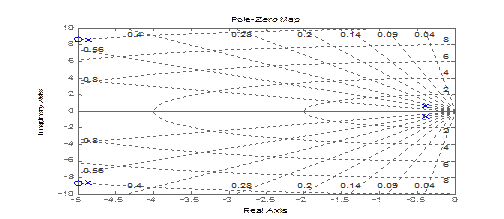
Дата добавления: 2021-12-14; просмотров: 602;











