Связь координат точек снимка и местности. Формулы взаимного перехода от одной системы координат к другой.

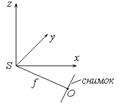
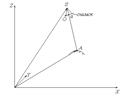Пусть из центра проекции S сделан снимок местн., на кот. отразилась т. мест-ти А в виде т. а. Вектор 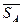обозначим через RSA. 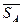= RSA. 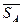= r. Введем вектор RА и RS., RSA=mr, где m – масштаб.

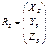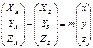RSA= RА - RS; RА - RS= mr. Это уравнение коллиниарности векторов. Перепишем его в координатном виде: ; ; XA-XS=mx; YA-YS=my; ZA-ZS=mz; Тогда, XA=XS+mx; YA=YS+my; 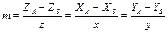; Тогда: 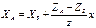; 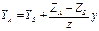Координаты точек снимка x, y, z даны в фотограмметрической системе координат, начало которой перенесено в точку фотографирования S. А снимок находится под наклоном к данной системе координат на углы α, ω, æ.

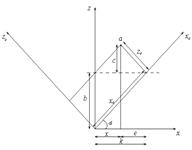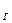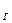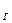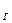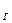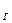В системе координат снимка координаты точки определяются следующими значениями xc, yc, zc=-f. Задача заключается в том, чтобы от координат xc, yc, zc= -f перейти к координатам x, y, z используя углы Эйлера α, ω, æ. Угол α – лежит в плоскости Z X , разворот осуществл. по осиY, угол ω – в пл-ти Y Z , разворот по оси X,угол χ - в пл-ти Y X , разворот по оси Z Покажем связь между данными системами координат на примере угла α:

Даны: xc, zс, α; Найти: x, z Решение: z=b+c , b=xcsinα , c=zccosα , z= xcsinα+ zccosα , x=k-е , k= xccosα , e= zcsinα , x= xccosα- zcsinα Таким образом: x= xccosα- zcsinα , z= xcsinα+ zccosα В общем виде это можно записать так: 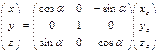Аналог данной формулы для угла ω будет следующим:

Для угла æ: 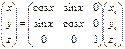Вводим обозначения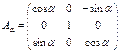

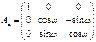
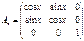
Тогда 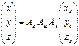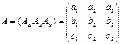Тогда вид формул связи координат соответствующих точек снимка и местности будет следующим: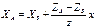 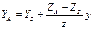Подставляя значения x, y, z в данные выражения найдем окончательный вид формул связи: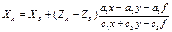

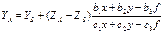
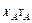-координаты точки А мест-ти, 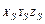- координаты центра проекции; X,Y,-f – координаты точек на наклон. снимке.