Обработка теодолитного хода
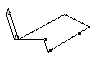 1. Обработка теодолитного хода.
1. Обработка теодолитного хода.

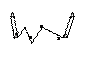 Теодолитный ход - ломаная линия, закрепленная на местности вдоль которой измерены горизонтальные углы и длины линии. Бывает замкнутый и разомкнутый. Замкнутый: измеряемыми величинами явл-я углы β1, β2… ,S1,S2… а также привязочный угол β0. Известны корд. Исходных точек А и В. Необходимо найти координаты точек 1,2,3… Разомкнутый: Измеренные величины β1, β2… ,S1,S2… Исх коорд. точек А,В,С,D. Найти корд. 1,2,3.При создании съемочного обоснования необходимо определять коорд. определяемых пунктов, в основе этого лежит прямая геодезическая задача. Даны: Ха,Уа,α,S.Определить Х,У. Решение: х1=ха+∆х,у1=уа+∆у ∆х/S=соsα, ∆х=S*cosα. ∆у=S*sinα. х1=ха+ S*cosα, у1=уа+ S*sinα.Обратная геод задача: Известны координаты точек ха,уа,хв,ув, найти дирекционный угол стороны α и длину S. tg α= ∆y/ ∆x, α=arctg(∆y/∆x),
Теодолитный ход - ломаная линия, закрепленная на местности вдоль которой измерены горизонтальные углы и длины линии. Бывает замкнутый и разомкнутый. Замкнутый: измеряемыми величинами явл-я углы β1, β2… ,S1,S2… а также привязочный угол β0. Известны корд. Исходных точек А и В. Необходимо найти координаты точек 1,2,3… Разомкнутый: Измеренные величины β1, β2… ,S1,S2… Исх коорд. точек А,В,С,D. Найти корд. 1,2,3.При создании съемочного обоснования необходимо определять коорд. определяемых пунктов, в основе этого лежит прямая геодезическая задача. Даны: Ха,Уа,α,S.Определить Х,У. Решение: х1=ха+∆х,у1=уа+∆у ∆х/S=соsα, ∆х=S*cosα. ∆у=S*sinα. х1=ха+ S*cosα, у1=уа+ S*sinα.Обратная геод задача: Известны координаты точек ха,уа,хв,ув, найти дирекционный угол стороны α и длину S. tg α= ∆y/ ∆x, α=arctg(∆y/∆x),
S= √(∆y)2+(∆x)2.
Обработка замкнутого теод.хода.В данном теод ходе измерены внутренние углыполигона. Теоретическая сумма углов:Σ 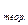 =180(n-2). Σ
=180(n-2). Σ 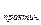 = β1+ β2+…+ β n. Разность этих значений называется невязкойтеод хода. Это угловая невязка ƒβ=Σпр.-Σтеор. ƒβдоп=1'√ n. Если ƒβ≤ƒβдоп то вычисляют поправки в углы. U β=- ƒβ/ n. Исправленные углы β'i= βi+U' β.Контроль:
= β1+ β2+…+ β n. Разность этих значений называется невязкойтеод хода. Это угловая невязка ƒβ=Σпр.-Σтеор. ƒβдоп=1'√ n. Если ƒβ≤ƒβдоп то вычисляют поправки в углы. U β=- ƒβ/ n. Исправленные углы β'i= βi+U' β.Контроль:
Σ β'i=180(n-2).По исправленным углам вычисляем дирекционные.При правых измеренных они вычисляются как α 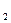 =α
=α 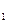 +(180-β). При левых α
+(180-β). При левых α 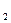 =α
=α 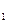 +( β-180).Увязка приращений координат:Если предположить что приращения координат ∆х1, ∆х2… безошибочны, то х
+( β-180).Увязка приращений координат:Если предположить что приращения координат ∆х1, ∆х2… безошибочны, то х 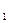 =х
=х 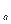 + ∆x
+ ∆x 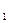 , х
, х 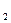 = х
= х 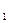 +∆ х
+∆ х 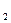 , х
, х 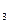 =х
=х 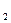 +∆x
+∆x 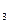 , х
, х 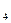 =х
=х 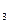 +∆x
+∆x 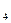 , х
, х 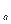 =х
=х 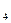 + ∆x
+ ∆x 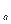 . Поскольку у нас есть вычисленные приращения координат Σ∆xпр= ∆x1+∆x2+∆x3+…, ƒх= Σ∆xпр- Σ∆xтеор=Σ∆xпр, ƒу=Σ∆yпр. ƒs=√ƒх2+ƒу2. ƒs/Σs=1/Σs:ƒs . Если ƒs допустима (f
. Поскольку у нас есть вычисленные приращения координат Σ∆xпр= ∆x1+∆x2+∆x3+…, ƒх= Σ∆xпр- Σ∆xтеор=Σ∆xпр, ƒу=Σ∆yпр. ƒs=√ƒх2+ƒу2. ƒs/Σs=1/Σs:ƒs . Если ƒs допустима (f 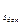 ≤
≤ 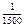 ), то вычисляем поправки в приращения корд. пропорционально длинам сторон U∆xi= - (Si/ΣS)*ƒ
), то вычисляем поправки в приращения корд. пропорционально длинам сторон U∆xi= - (Si/ΣS)*ƒ 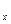 , U∆уi= - (Si/ΣS)*ƒ
, U∆уi= - (Si/ΣS)*ƒ 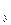 . Вычисляются исправленные приращения ∆xi'=∆xi +U∆xi, ∆уi'= ∆уi +U∆уi. По исправленным приращениям вычисляются корд.точек.Обработка разомкнутого теод. хода.Если измерены левые по ходу горизонтальные углы, то: α1=αн+β1-180,…, αк=αн-1+ βn-180, отсюда β1=α1+180-αн,…, βк= αк+180 – αn-1.Если сложить вычисленные углы, то Σ β=- αн+180*n+ αк= αк+180* n- αн. Это есть теор. сумма углов в раз. теод. ходе с левыми угл. Если рассмотреть теод. ход с правыми гориз углами. α1= αн+180- β1,…, αк= α n-1+180-β
. Вычисляются исправленные приращения ∆xi'=∆xi +U∆xi, ∆уi'= ∆уi +U∆уi. По исправленным приращениям вычисляются корд.точек.Обработка разомкнутого теод. хода.Если измерены левые по ходу горизонтальные углы, то: α1=αн+β1-180,…, αк=αн-1+ βn-180, отсюда β1=α1+180-αн,…, βк= αк+180 – αn-1.Если сложить вычисленные углы, то Σ β=- αн+180*n+ αк= αк+180* n- αн. Это есть теор. сумма углов в раз. теод. ходе с левыми угл. Если рассмотреть теод. ход с правыми гориз углами. α1= αн+180- β1,…, αк= α n-1+180-β 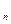 . Если вычислить углы, то β1= αн+180- α1, …, βn= α n-1+180- αк. Σβ= αн+180*n- αк.Это теор сумма углов при правых углах. Для левых и правых в дальнейшем вычисляется невязка. ƒβ= Σβпр- Σβтеор.;Σβпр= β1+β2+β3+…, Σβтеор.лев.= αк+180*n-αn, Σβтеор.прав.= αn+180*n-αк, U
. Если вычислить углы, то β1= αн+180- α1, …, βn= α n-1+180- αк. Σβ= αн+180*n- αк.Это теор сумма углов при правых углах. Для левых и правых в дальнейшем вычисляется невязка. ƒβ= Σβпр- Σβтеор.;Σβпр= β1+β2+β3+…, Σβтеор.лев.= αк+180*n-αn, Σβтеор.прав.= αn+180*n-αк, U 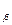 =-ƒ
=-ƒ 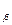 /n исправленные углы β'=β+ U
/n исправленные углы β'=β+ U 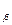 .Вычисление и увязка приращения координат.По исправленным углам вычисляем дирекционные углы. αi= αi-1+180- βi, ∆xi=Si*cosαi, ∆yi=Si*sinαi. Приращение координат м/у исходными корд. В и С можно найти дважды.1. Σ∆xпр=∆x1+∆x2+… 2. Σ∆xтеор.=Хс-Хв=Хк-Хн. Анологично по У. Соответствующие теорет. и пр. суммы должны быть м/у собой одинаковы, но из-за ошибок в измерениях, м/у ними будет разница,кот наз. невязка. ƒх= Σ∆Хпр- Σ∆Хтеор. ƒу= Σ∆Упр- Σ∆Утеор. ƒs=√ƒх2+ƒу2. Если ƒs допустима, то вычисляем поправки в приращения корд из расчета, что периметру соответствует поправка. U∆xi=-( ƒхi/ Σs)*Si, U∆уi=-( ƒуi/ Σs)*Si. ∆x'i=∆xi+U∆xi, ∆у'i=∆уi+U∆уi. Х1=Хн+∆Х1, Х2=Х1+∆Х2…контроль Хк=Хn-1+∆Хn. Анологично с У.
.Вычисление и увязка приращения координат.По исправленным углам вычисляем дирекционные углы. αi= αi-1+180- βi, ∆xi=Si*cosαi, ∆yi=Si*sinαi. Приращение координат м/у исходными корд. В и С можно найти дважды.1. Σ∆xпр=∆x1+∆x2+… 2. Σ∆xтеор.=Хс-Хв=Хк-Хн. Анологично по У. Соответствующие теорет. и пр. суммы должны быть м/у собой одинаковы, но из-за ошибок в измерениях, м/у ними будет разница,кот наз. невязка. ƒх= Σ∆Хпр- Σ∆Хтеор. ƒу= Σ∆Упр- Σ∆Утеор. ƒs=√ƒх2+ƒу2. Если ƒs допустима, то вычисляем поправки в приращения корд из расчета, что периметру соответствует поправка. U∆xi=-( ƒхi/ Σs)*Si, U∆уi=-( ƒуi/ Σs)*Si. ∆x'i=∆xi+U∆xi, ∆у'i=∆уi+U∆уi. Х1=Хн+∆Х1, Х2=Х1+∆Х2…контроль Хк=Хn-1+∆Хn. Анологично с У.
Дата добавления: 2021-12-14; просмотров: 444;











