Решения задач Главы 5
Решение задачи 9
Поскольку представлены данные по двум выборкам, мы выбираем критерий Фишера для оценки различий в процентных долях. Будем считать "эффектом" преобладание левого глаза. В исследовании Т.А. Доброхотовой и Н.Н. Брагиной высказывалось предположение о феномене предвосхищения у левшей, их способности к "зеркальному" отражению не только пространства, но и времени, выражающейся в прогностических возможностях и особого рода проницательности (Доброхотова Т.А., Брагина Н.Н., 1994). Интересно поэтому сопоставить выборки прямо по эффекту левшества.
Построим четырехпольную таблицу.
Таблица 9.20
Четырехпольная таблица для расчета критерия φ* при сопоставлении студентов-психологов (nj=14) и студентов-медиков (п2=100) по прицельной способности глаз
| Группы | "Есть эффект" преобладание левого глаза | "Нет эффекта" преобладание правого глаза | Суммы | ||
| Количество испытуемых | % доля | Количество испытуемых | % ДОЛЯ | ||
| 1 группа -студенты - психологи | 42,9% | 57,1% | |||
| 2 группа -студенты - медики | 19% | 81% | |||
| Суммы |
Сформулируем гипотезы.
H0: Доля лиц с преобладанием левого глаза в группе студентов-психологов не больше, чем в группе студентов-медиков.
H1: Доля лиц с преобладанием левого глаза в группе студентов-психологов больше, чем в группе студентов-медиков. По Табл. XII Приложения 1 определяем φ1 и φ2: Ф1(42.9%)=1.430; ф2(19%)=0,902 Подсчитываем эмпирическое значение φ *:
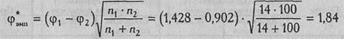
Критические значения φ * нам известны:
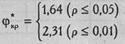
φ* эмп > φ* кр (р≤0,05)
Можно и более точно определить уровень значимости для φ эмп=1,84: р=0,033.
Ответ: H0 отклоняется. Доля лиц с преобладанием левого глаза в.группе студентов-психологов больше, чем в группе студентов-медиков (р=0,0ЗЗ).
Возможно, в данном исследовании произошло то, что называется "самоисполняющимися предсказаниями". Студенты-психологи перед началом опыта узнали об идее Брагиной и Доброхотовой о возможных прогностических способностях лиц с преобладанием левшества. Желание выявить у себя столь важные способности могло исказить результаты, несмотря на достаточную объективность карандашного теста.
Решение задачи 10
Поскольку сопоставляются две группы, мы применяем критерий φ * Фишера.
Вопрос 1: Можно ли считать, что милиционеры патрульно-постовой службы в большей степени склонны продолжить разговор с агрессором, чем другие граждане?
В данном случае нам легко определить, что будет критерием для разделения испытуемых на тех, у кого "есть эффект", и тех, у кого "нет эффекта".
Признак принимает всего два значения: разговор продолжен -разговор не продолжен. Ориентируясь на вопрос задачи, будем считать, что "эффект есть", если разговор продолжен, и что "эффекта нет", если разговор не продолжен.
Создадим четырехклеточную таблицу.
Таблица 9.21
Четырехклеточная таблица для сопоставления милиционеров (n1=25) и гражданских лиц (n 2=25) по показателю продолжения разговора с агрессором
| Группы | "Есть эффект" разговор продолжен | "Нет эффекта" разговор не продолжен | Суммы | ||
| Количество испытуемых | % ДОЛЯ | Количество испытуемых | % ДОЛЯ | ||
| 1 группа -милиционеры | 60% | 40% | |||
| 2 группа -гражданские лица | 28% | 72% | |||
| Суммы |
Сформулируем гипотезы.
H0: Доля лиц, продолживших разговор с агрессором, в группе милиционеров не больше, чем в группе гражданских лиц.
H1: Доля лиц, продолживших разговор с агрессором, в группе милиционеров больше, чем в группе гражданских лиц.
Определим значения угла φ для каждой из сопоставляемых процентных долей:
φ 1(6О%)=1,772
φ 2(28%)=1,115
Рассчитаем эмпирическое значение φ *:
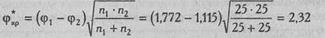
Как мы помним, критические значения φ * для всех щ, п? равны:
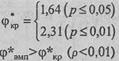
Оmвem: H0 отвергается. Принимается H1. Доля лиц, продолживших разговор с агрессором, в группе милиционеров больше, чем в группе гражданских лиц (р<0,01).
Вопрос 2: Можно ли утверждать, что милиционеры склонны отвечать агрессору более примирительно, чем гражданские лица?
Ориентируясь на вопрос задачи, будем считать, что "эффект есть", если испытуемый дал неагрессивный, примирительный ответ, и что "эффекта нет", если испытуемый дал агрессивный ответ.
Создавая четырехклеточную таблицу, мы помним о том, что объемы выборок несколько сократились, поскольку в них были испытуемые, уклонившиеся от продолжения разговора с агрессором.
Таблица 9.22
Четырехклеточная таблица для сопоставления долей неагрессивных ответов в группах милиционеров и гражданских лиц
| Группы | "Есть эффект" неагрессивный ответ | "Нет аффекта" агрессивный ответ | Суммы | ||
| 1 группа -милиционеры | (66,7%) | (33,3%) | |||
| 2 группа -гражданские лица | (42,9%) | (57,1%) | |||
| Суммы |
Мы можем далее использовать угловое преобразование Фишера, то есть критерий φ *, поскольку ни одна из сопоставляемых долей не равна 0. При уменьшении выборок угроза появления нуля в какой-либо из ячеек, естественно, возрастает, поэтому контроль необходим (см. ограничение 1).
Сформулируем гипотезы. H0: Доля неагрессивных ответов в группе милиционеров не больше, чем
в группе гражданских лиц. H1: Доля неагрессивных ответов в группе милиционеров больше, чем в
группе гражданских лиц. Определим значения φ1 и φ2 и рассчитаем эмпирическое значение φ *:
φ 1(66,7%)=1,911
φ 2(42,9%)=1,428
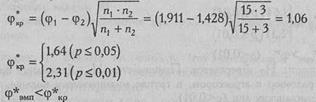
Ответ: H0 принимается. Доля неагрессивных ответов в группе милиционеров не больше, чем в группе гражданских лиц. Как свидетельствует Табл.ХШ Приложения 1, полученное значение меньше даже критического значения, соответствующего уровню значимости р<0,10.
Вспомним, однако, что мы включили в четырехклеточную таблицу только тех испытуемых обеих групп, которые вступили в разговор с агрессором. Если же подсчитывать доли агрессивных и неагрессивных реакций по отношению к общему количеству испытуемых в данной выборке, то результат получится достоверным (φ *эмп=2,34; р<0,01).
Именно так и поступил автор данного исследования. Это позволило ему сделать вывод, что милиционеры предпочитают неагрессивные ответы, поскольку, по-видимому, это дает время и возможность оценить степень опасности нападающего субъекта для окружающих. Срабатывает профессиональный инстинкт (Кузнецов А.А., 1991).
Решение задачи 11
Поскольку сравниваются две выборки, выбираем критерий φ * Фишера. Однако "на глаз" трудно решить, какая команда врачей должна считаться большей по составу, а какая - меньшей. Нам необходимо найти точку, в которой накапливаются максимальные различия между двумя распределениями, для того, чтобы применение критерия φ * было максимально эффективным. Для этого вначале используем алгоритм определения максимальной разности между накопленными частостями, используемый в критерии λКолмогорова-Смирнова (Алгоритм 15).
Результаты применения алгоритма представлены в Табл. 9.23
Таблица 9.23
Выявление точки максимальной разности между эмпирическими распределениями "количества партнеров у врачей с фондами (n1=49) и врачей без фондов (n 2=28)
| количество партнеров | Эмпирические частоты | Эмпирические частости | Накопленные эмпирические частости | Разность | ||||
| f1 | f2 | f*1 | f*2 | ∑f*1 | ∑f*2 | (∑f*1 - ∑f*2) | ||
| 2 и менее партнеров | 0,041 | 0,536 | 0,041 | 0,536 | 0,495 | |||
| 3-4 партнера 5-6 партнеров | 0,122 0,551 | 0,179 0,286 | 0,163 0,714 | 0,715 1,000 | 0,286 | |||
| 7 и более партнеров | 0,286 | 1,000 | 1,000 | |||||
| Суммы | 1,000 | 1,000 |
Как видно из Табл. 9.23, максимальная разность накопленных частостей падает на 2-й разряд (3-4 партнера). Поскольку вопрос в задаче касается предположения о том, что в приемных с фондами работают большие по составу команды врачей, чем в приемных без фондов, будем считать, что если партнеров более 4-х, то "эффект есть", а если партнеров 4 и менее, то "эффекта нет". Построим соответствующую четырехклеточную таблицу и определим % доли "эффекта" в каждой из двух выборок.
Таблица 9.24
Четырехклеточная таблица для подсчета критерия φ * при сопоставлении выборок врачей с фондами (n1=49) и врачей без фондов (п2=28) по признаку количества партнеров
| Группы | "Есть эффект" более 4 партнеров | "Нет эффекта" не более 4 партнеров | Суммы | ||
| 1 группа -врачи с фондами | (83,7%) | (16,3%) | |||
| 2 группа -врачи без фондов | (28,6%) | (71,4%) | |||
| Суммы |
Сформулируем гипотезы.
H0: Доля лиц, имеющих более 4-х партнеров, в выборке врачей с фондами не больше, чем в выборке врачей без фондов.
H1: Доля лиц, имеющих более 4-х партнеров, в выборке врачей с фондами больше, чем в выборке врачей без фондов. По Табл. XII Приложения 1 определяем углы φ:
φ 1(83,7%)=2,310
φ 2(28,6%)=1,129
Рассчитаем эмпирическое значение критерия φ *:
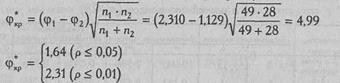
По Табл. XIII Приложения 1 определяем, какому уровню значимости соответствует эта величина φ *: р<0,001.
φ* эмп > φ* кр (p<0,001)
Ответ: H0 отклоняется. Принимается H1. Доля лиц, имеющих более 4-х партнеров, в выборке врачей с фондами больше, чем в выборке врачей без фондов (р<0,001).
Фирма с высокой степенью уверенности может ориентироваться на эту тенденцию в построении своей стратегии продвижении товара. Но то, как она будет ее учитывать, уже выходит за рамки данной статистической задачи.
Решение задачи 12
Обследована одна выборка испытуемых, поэтому останавливаем выбор на биномиальном критерии т. В параграфе 4.2, посвященному методу χ2, эта задача предположительно должна была решаться с помощью критерия χ2. Однако, поскольку количество наблюдений n<300, а вероятность выбора каждой из дорожек при равновероятном выборе составляет ½, т.е. P=Q=0,50, мы можем воспользоваться биномиальным критерием, который несравненно проще в использовании, чем критерий χ2. Воспроизведем таблицу частот.
Таблица 9.25
Эмпирические частоты выбора правой и левой симметричных дорожек (n=70)
| Выбрана правая дорожка | Выбрана левая дорожка | Суммы |
Сформулируем гипотезы.
H0: Частота выбора правой дорожки не превышает частоты, которая соответствует вероятности случайного выбора.
H1: Частота выбора правой дорожки превышает частоту, которая соответствует вероятности случайного выбора.
Определим теоретическую частоту выбора одной из дорожек при случайном выборе:
fтеор=n·р =70·0,50=35
Поскольку fэмп > fтеор, используем биномиальный критерий m, a не его "зеркальное отражение" (критерий знаков G).
По Табл. XIV Приложения 1 определяем критические значения m для n=70:
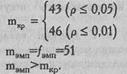
Ответ: H0 отклоняется. Принимается H1. Частота предпочтения правой дорожки превышает частоту, которая соответствует вероятности случайного выбора (р<0,01).
Наблюдатель может обоснованно утверждать, что из данных двух симметричных дорожек чаще выбирается правая. Чем это объясняется— уже другой вопрос, выходящий за рамки задачи (см. п. 4.2).
[1] Стохастическая означает вероятностная. Связи между случайными явлениями называют вероятностными, или стохастическими связями (Суходольский Г. В., 1972, с. 52). Этот термин подчеркивает их отличие от детерминированных или функциональных связей в физике или математике (связь площади треугольника с его высотой и основанием, связь длины окружности с ее радиусом и т. п.). В функциональных связях каждому значению первого признака всегда соответствует (в идеальных условиях) совершенно определенное значение другого признака (Плохинский Н.А., 1970, с. 41). В корреляционных связях каждому значению одного признака может соответствовать определенное распределение значений другого, признака, но не определенное его значение.
[2] Обычно рекомендуется всегда меньшему значению приписывать меньший ранг (см. Пример 1). В данном случае самая значимая ценность получает меньший ранг. Для подсчета коэффициента это несущественно. Главное, чтобы ранжирование было в обоих рядах однонаправленным.
[3] В исследовании М.Э. Раховой были выявлены виды страха, отсутствующие в перечне Вольпе, например, страх за благополучие близких (1-й ранг), неизвестности (5-й ранг), нападения (8-й ранг) и др. Однако в данном примере в ранжировании участвуют только 20 страхов из перечня Вольпе, поскольку мы можем подсчитывать коэффициент корреляции лишь между теми признаками, которые измерены в обеих выборках.
[4] Введение этого условия диктовалось тем, что в непосредственно предшествовавших исследованию выборах 52% электората составляли лица старше 55 лет.
Дата добавления: 2016-06-05; просмотров: 1692;











