Решения задач Главы 4
Решение задачи 6
Вопрос 1: Можно ли утверждать, что разные картины методики Хекхаузена обладают разной побудительной силой в отношении мотивов: а) "надежда на успех"; б) "боязнь неудачи"?
Для того, чтобы ответить на этот вопрос, необходимо сопоставить распределение реакций "надежда на успех" и реакций "боязнь неудачи" с равномерным распределением. Тем самым мы проверим, равномерно ли распределяются реакции "надежды на успех" по шести картинам и равномерно ли распределяются реакции "боязни неудачи" по шести картинам.
Количество наблюдений достаточно велико, чтобы мы могли использовать любой из классических критериев - χ2 или λ. Однако, как мы помним, картины в данном исследовании предъявлялись разным испытуемым в разных последовательностях, следовательно, мы не можем говорить об однонаправленном изменении признака в какую-либо одну сторону: все разряды (картины) следуют друг за другом в случайном порядке. Это является веским основанием для применения критерия χ2 и отказа от критерия λ.
Рассмотрим оба аспекта поставленного вопроса последовательно.
А) Равномерно ли распределяются реакции "надежды на успех" по шести картинам методики Хекхаузена?
H0: Распределение реакций "надежды на успех" не отличается от равномерного распределения.
H1: Распределение реакций "надежды на успех" отличается от равномерного распределения.
Рассчитаем теоретические частоты для равномерного распределения по формуле:
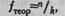
где n - количество наблюдений,
k - количество разрядов.
В данном случае количество наблюдений - это количество реакций "надежды на успех" у 113 испытуемых. Таких реакций зарегистрировано 580, следовательно, n =580. Количество разрядов - это количество стимульных картин, следовательно, k=6. Определяем fтеор:
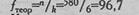
Количество степеней свободы V определяем по формуле:
v= k -l=6-l=5
Итак, поправка на непрерывность не нужна, мы можем производить все расчеты по общему алгоритму. Они представлены в Табл.9.11.
Таблица 9.11
Расчет критерия χ2 при сопоставлении распределения реакций "надежды на успех" по 6 картинам с равномерным распределением
| Разряды-картины методики | Эмпирические частоты реакций "надежды на успех" fэ | Теоретические частоты реакции "надежды на успех" fт | fэ- fт | (fэ- fт)2 | (fэ- fт)2/ fт | |
| "Мастер измеряет деталь" "Преподаватель и ученик" "В цехе у машины" "У двери директора" "Человек в бюро" "Улыбающийся юноша" | 96,67 96,67 96,67 96,67 96,67 96,67 | 9,33 5,33 11,33 -46,67 2,33 18,33 | 87,05 28,41 128,37 2178,09 5,43 335,99 | 0,90 0,29 1,33 22,53 0,06 3,48 | ||
| Суммы | 28,59 | |||||
По Табл. IX Приложения 1 определяем критические значения χ2 дляv=5:
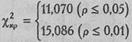
Построим "ось значимости".
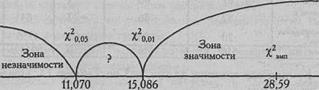
χ2эмп = 28,59
χ2эмп > χ2кр
Ответ: H0 отклоняется. Принимается H1. Распределение реакций "надежды на успех" по шести картинам методики Хекхаузена отличается от равномерного распределения (р<0,01).
Б) Равномерно ли распределяются реакции "боязни неудачи" по шести картинам методики Хекхаузена?
H0: Распределение реакций "боязни неудачи" не отличается от равномерного распределения.
H1: Распределение реакций "боязни неудачи" отличается от равномерного распределения.
В данном случае количество наблюдений - это число реакций "боязни неудачи", следовательно, n=516; количество разрядов - это число стимульных картин, как и в предыдущем случае, следовательно, k=6. Определяем fтеор
fтеор =516/6=86
Количество степеней свободы v=k—1=6—1=5. Поправка на непрерывность здесь тоже, естественно, не нужна.
Все дальнейшие расчеты проделаем по алгоритму в таблице.
Таблица 9.12
Расчет критерия при сопоставлении распределения реакций "боязни неудачи" по 6 картинам с равномерным распределением
| Разряды-картины методики | Эмпирические частоты реакций "боязни неудачи" fэ | Теоретические частоты реакции "боязни неудачи" fт | fэ- fт | (fэ- fт)2 | (fэ- fт)2/ fт | |
| "Мастер измеряет деталь" "Преподаватель и ученик" "В цехе у машины" "У двери директора" "Человек в бюро" "Улыбающийся юноша" | -52 -29 -66 | 31,44 102.74 31,44 0.01 9.78 50,65 | ||||
| Суммы | 226,06 | |||||
Критические значения χ2при v=5 по Таблице IX Приложения 1 нам уже известны:
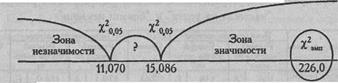
χ2эмп > χ2кр
Ответ: H0 отклоняется. Принимается H1. Распределение проявлений "боязни неудачи" по шести стимульным картинам отличается от равномерного распределения (р<0,01).
Итак, реакции "надежды на успех" и реакции "боязни неудачи" неравномерно проявляются в ответ на 6 стимульных картин. Однако это еще не означает, что эти картины являются неуравновешенными по направленности воздействия. Может оказаться так, по крайней мере теоретически, что одни и те же картины вызывают большинство реакций обоих типов, а другие картины почти не вызывают реакций или вызывают их достоверно меньше. В этом случае оба эмпирических распределения отличались бы от равномерного, но не различались бы между собой.
Проверим, различаются ли картины теперь уже не по количеству вызываемых реакций, а по их качеству, то есть вызывают ли одни картины скорее реакции "надежды на успех", а другие - реакции "боязни неудачи"
Вопрос 2: Можно ли считать стимульный набор методики Хекхаузена неуравновешенным по направленности воздействия?
Решим эту задачу двумя способами: а) путем сравнения распределения реакций "надежда на успех" с распределением реакций "боязнь неудачи" по 6-и картинам; б) путем сопоставления распределения реакций на каждую картину с равномерным распределением.
Выясним, совпадают ли распределения реакций по двум картинам. Для этого сформулируем гипотезы.
H0: Распределения реакций "надежда на успех" и реакций "боязнь неудачи" не различаются между собой.
H1: Распределения реакций "надежда на успех" и "боязнь неудачи" различаются между собой.
Для того, чтобы облегчить себе задачу подсчета теоретических частот, воспроизведем таблицу эмпирических частот и дополним ее.
Таблица 9.13
Эмпирические и теоретические частоты распределения реакций "надежда на успех" и "боязни неудачи"
| Разряды - картины | Эмпирические частоты | Суммы | Теоретические частоты | Суммы | |||||||
| Реакций "надежда на успех" | Реакций "боязнь неудачи" | Реакций "надежда на успех" | Реакций "боязнь неудачи" | ||||||||
| "Мастер измеряет деталь" "Преподаватель и ученик" "В цехе у маши- "У двери директора" "Человек в бюро" "Улыбающийся юноша" | А В д ж и л | Б Г Е К M | 129,1 149,2 75,1 72,5 82,6 71,4 | А В Д Ж И Л | 114,9 132,8 66,9 64,5 73,4 63,6 | Б Г Е К М | |||||
| Суммы | |||||||||||
Расчет теоретических частот осуществляется по известной нам формуле:

Произведем расчеты.
fА теор=244·580/1096=129,1
fБ теор=244·516/1096=114,9
fВ теор=282·580/1096=149,2
fГ теор=282·516/1096=132,8
fД теор=142·580/1096=75,1
fЕ теор=142·516/1096=66,9
fЖ теор=137·580/1096=72,5
fЗ теор=137·516/1096=64,5
fИ теор=156·580/1096=82,6
fК теор=156·516/1096=73,4
fЛ теор=135·580/1096=71,4
fМ теор=135·516/1096=63,6
По Табл. 9.13 мы видим, что сумма всех теоретических частот равна общему количеству наблюдений, а попарные суммы теоретических частот по строкам равны суммам наблюдений по строкам.
Расчеты критерия χ2будем производить по известному алгоритму. Поправка на непрерывность не вносится, так как v>1:
v=(r-l)(c-l)=(6-l)(2-l)=5
Результаты всех операций по Алгоритму 13 представлены в Табл. 9.14.
Таблица 9.14
Расчет критерия χ2при сопоставлении эмпирических распределений реакций "надежды на успех" (НУ) и "боязни неудачи" (БН)
| Ячейки таблицы частот | Эмпирическая частота fэ | Теоретическая частота fт | fэ- fт | (fэ- fт)2 | (fэ- fт)2/ fт | |
| А | 129,1 | -23,1 | 533,61 | 4,13 | ||
| Б | 114,9 | 23,1 | 533,61 | 4,64 | ||
| В | 149,2 | -47,2 | 2227,84 | 14,93 | ||
| Г | 132,8 | 47,2 | 2227,84 | 16,78 | ||
| Д | 75,1 | 32,9 | 1082,41 | 14,41 | ||
| Е | 66,9 | -32,9 | 1082,41 | 16,18 | ||
| Ж | 72,5 | -22,5 | 506,25 | 6,98 | ||
| 64,5 | 22,5 | 506,25 | 7,85 | |||
| И | 82,6 | 16,4 | 268,96 | 3,26 | ||
| К | 73,4 | -16,4 | 268,96 | 3,66 | ||
| Л | 71,4 | 43,6 | 1900,96 | 26,62 | ||
| М | 63,6 | -43,6 | 1900,96 | 29,89 | ||
| Суммы , | 149,33 |
Критические значения χ2при v=5 нам уже известны:
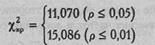
Построим "ось значимости".
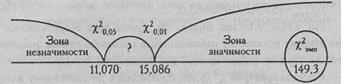
χ2эмп > χ2кр
Ответ: H0 отвергается. Принимается H1. Распределения реакций "надежды на успех" и "боязни неудачи" различаются между собой.
Теперь выясним, совпадают ли распределения реакций по каждой картине. Сформулируем гипотезы.
H0: Реакции двух видов в ответ на картину №1 (№2, №3 ... №6) распределяются равномерно.
H1: Реакции двух видов в ответ на картину №1 (№2, №3 ... №6) распределяются неравномерно.
Реакции "надежды на успех" будем обозначать как НУ, реакции "боязни неудачи" - как БН.
Подсчитаем теоретические частоты для каждой из шести картин, по формуле:
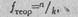
где n общее количество реакций обоих направлений на данную картину; k - количество разрядов, в данном случае количество видов реакции (k =2).
f1 теор =244/2=121;
f2 теор =282/2=141;
f3 теор =142/2=71;
f4 теор =137/2=68,5
f5 теор =156/2=78
f6 теор =135/2=67,5
В данном случае число степеней свободы v=l:
v=k—1=2—1=1.
Следовательно, мы должны сделать во всех шести случаях поправку на непрерывность. Проведем расчеты отдельно для каждой картины (см. Табл. 9.15).
Таблица 9.15
Расчет критерия χ2при сопоставлении распределений реакций на каждую из шести картин с равномерным распределением
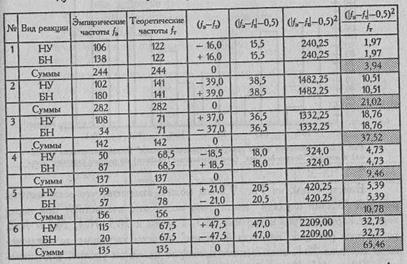
Определим по Табл. IX Приложения 1 критические значения для v=l:
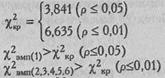
Ответ: H0 отклоняется для всех картин. H1принимается для картин 2, 3, 4, 5 и 6: реакции двух видов в ответ на эти картины распределяются неравномерно.
Если представить данные графически (Рис. 9.2), то легко можно видеть, что картины №6, №3 и №5 вызывают достоверно больше реакций "надежды на успех", а картины №2, №1 и №4 - достоверно больше реакций "боязни неудачи".
Стимульный набор методики Х. Хекхаузена оказался неуравновешенным по направленности стимулирующего воздействия.
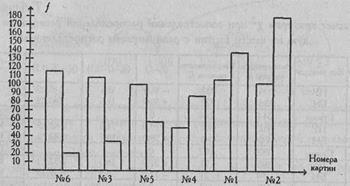
Рис. 9.2. Соотношения частот реакций "надежда на успех" (незаштрнхованные столбн-ки) н реакций "боязнь неудачи" (заштрихованные столбики) по разным картинам методики Х.Хекхаузена
Вместе с тем, из Рис. 9.2 мы можем заметить, что если частоты реакций "боязни неудачи" достаточно монотонно возрастают при переходе от картины №6 к картине №3, а затем к №5, №4, №1 и №2, то частоты реакций "надежда на успех" по всем картинам, за исключением картины №4, оказываются примерно на одном уровне, в диапазоне от 99 до 115. Каждый исследователь сам для себя решает вопрос о том, что для него важнее - абсолютные показатели стимулирующего воздействия или их соотношения. Метод у} поможет ему решить задачи и первого, и второго типа.
Решение задачи 7
Вопрос 1: Можно ли утверждать, что распределение запретов не является равномерным?
Поскольку количество разрядов (запретов) k>3, иперечень из пяти запретов представляет собой номинативную шкалу, мы можем использовать только критерий χ2.
Если бы участники тренинга называли разные запреты с одинаковой частотой, то каждый из пяти запретов встречался бы равновероятно с остальными.
Сформулируем гипотезы.
H0: Распределение частот встречаемости пяти запретов не отличаетсяот равномерного распределения.
H1: Распределение частот встречаемости пяти запретов отличается от равномерного распределения.
Определим fтеор по формуле:
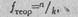
где n - общее количество наблюдений, в данном случае названных запретов (n =281); k - количество категорий запретов (k =5).
fтеор =281/5=56,2
Определим число степеней свободы v:
v = k -l=5-l=4.
Поправки на непрерывность делать не требуется. Все расчеты представим в таблице, строго следуя Алгоритму 13.
Таблица 9.16
Расчет критерия χ2при сопоставлении эмпирического распределения частот встречаемости 5-и психологических запретов с равномерным распределением
| Разряды - вид запрета | Эмпирическая частота fэ | Теоретическая частота fт | fэ- fт | (fэ- fт)2 | (fэ- fт)2/ fт |
| 1, Не давай психологических поглаживаний 2. Не принимай... 3. Не проси... 4. Не отказывайся... 5. Не давай себе... | 56,2 56,2 56,2 56,2 56,2 | -12,2 -11,2 +41,8 +1,8 -20,2 | 148,8 125,4 1747,2 3,2 408,0 | 2,65 2,23 31,09 0,06 7,26 | |
| Суммы | 43,29 |
Определим критические значения χ2по Таблице IX Приложения 1 для v=4:
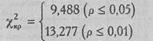
Построим "ось значимости"
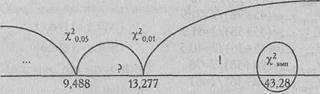
Ответ: χ2эмп > χ2кр (р≤0,01)
H0 отклоняется. Принимается H1. Распределение частот встречаемости пяти психологических запретов отличается от равномерного распределения (р<0,01).
Вопрос 2: Можно ли утверждать, что запрет "Не проси" встречается достоверно чаще остальных?
Для того, чтобы ответить на этот вопрос, мы можем попробовать сопоставить запрет "Не проси" последовательно со всеми остальными запретами, объединяя их попарно.
H0: Распределение выборов между запретами "Не проси" и "Не давай" не отличается от равномерного распределения.
H1: Распределение выборов между запретами "Не проси" и "Не давай" отличается от равномерного распределения.
Аналогичные гипотезы могут быть сформулированы для всех остальных пар запретов.
При сопоставлении двух запретов число разрядов k=2, следовательно, количество степеней свободы v=k—1=1. Это означает, что нам необходимо делать поправку на непрерывность.
Рассчитаем теоретические частоты для каждой из сопоставляемых пар запретов.
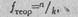
где п - сумма частот, приходящихся на данную пару запретов; k - количество сопоставляемых категорий запретов (k=2).
Определим теоретические частоты для всех возможных пар запретов.
fтеор 1-2=(44+45)/2=44,5
fтеор 1-3=(44+98)/2=71
fтеор 1-4=(44+58)/2=51
fтеор 1-5=(44+36)/2=40
fтеор 2-3=(45+98)/2=71,5
fтеор 2-4=(45+58)/2=51,5
fтеор 2-5=(45+36)/2=40,5
fтеор 3-4=(98+58)/2=78
fтеор 3-5=(98+36)/2=67
fтеор 4-5=(58+36)/2=47
Теперь подсчитаем значения критерия χ2 (Табл. 9.17).
Таблица 9.17. Расчет значений критерия при попарном сопоставлении частот запретов
| Сопоставляемые виды запретов | Эмпирические частоты fэ | Теоретические частоты fт | (fэ – fт) | (|fэ – fт| -O,5) | (|fэ – fт| -O,5)2 | (|fэ – fт| -O,5)2 __________ fт | |
| «Не давай» «Не принимай Суммы | 44,5 44,5 99,0 | -0,5 + 0,5 | |||||
| «Не давай» «Не проси» Суммы | 71,0 71,0 142,0 | -27,0 + 27,0 | 26,5 26,5 | 702,25 702,25 | 9,89 9,89 19,78 | ||
| «Не давай» «Не отказывайся» Суммы | 51,0 51,0 102,0 | -7,0 + 7,0 | 6,5 6,5 | 42,25 42,25 | 0,83 0,83 1.66 | ||
| «Не давай» «Не давай себе» Суммы | 40,0 40,0 80,0 | + 4,0 -4,0 | 3,5 3,5 | 12,25 12,25 | 0,31 0,31 0,62 | ||
| «Не принимай» «Не проси» Суммы | 71,5 71,5 143,0 | -26,5 +26,5 | 26,0 26,0 | 676,00 676,00 | 9,45 9,45 18,90 | ||
| «Не принимай» «Не отказывайся» Суммы | 51,5 51,5 103,0 | -6,5 + 6,5 | 6,0 6,0 | 36,00 36,00 | 0,70 0,70 1,40 | ||
| 2 5 | «Не принимай» «Не давай себе» Суммы | 40,5 40,5 81,0 | + 4,5 -4,5 | 4,0 4,0 | 16,00 16,00 | 0,40 0,40 0,80 | |
| 3 4 | «Не проси» «Не отказывайся» Суммы | 78,0 78,0 156,0 | + 20,0 -20,0 | 19,5 19,5 | 380,25 380,25 | 4,88 4,88 9,76 | |
| 3 5 | «Не проси» «Не давай себе* Суммы | 67,0 67,0 134,0 | + 31,0 -31,0 | 30,5 30,5 | 930,25 930,25 | 13,88 13,88 27,76 | |
| 4 5 | «Не отказывайся» «Не давай себе» Суммы | 47,0 47,0 94,0 | + 11,0 -11,0 | 10,5 10,5 | 110,25 110,25 | 2,35 2,35 4,70 |
Определим критические значения χ2для v =l:

Построим "ось значимости".
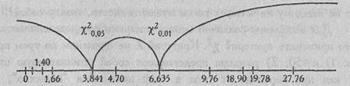
Мы видим, что в некоторых случаях χ2эмп > χ2кр, а в некоторых - χ2эмп < χ2кр.
Мы можем суммировать полученные данные, построив матрицу, в которой какими-либо знаками будет отмечено, являются ли различия между данной парой запретов достоверными или недостоверными. Например, это могут быть указания на уровень значимости различий.
| Запреты | 1 запрет 2 запрет 3 запрет 4 запрет 5 запрет | ||||
| 1 запрет | — | — | p<0,01 | — | — |
| 2 запрет | — | р<0,01 | — | — | |
| 3 запрет | — | р<0,01 | р<0,01 | ||
| 4 запрет | — | p<0,05 | |||
| 5 запрет | — |
Итак, выявлены достоверные различия в частоте встречаемости запрета 3 по сравнению со всеми остальными запретами (р<0,01 во всех четырех случаях) и запрета 4 по сравнению с запретом 5 (р<0,05).
Ответ: Hq отклоняется для пар запретов 1—3, 2—3, 3—4, 3—5 (р<0,01) и пары 4—5 (р<0,05). Запрет "Не проси психологических поглаживаний от других людей" встречается достоверно чаще, чем все остальные четыре запрета (р<0,01). Запрет "Не давай психологических поглаживаний самому себе" встречается реже, чем запрет "Не отказывайся от психологических поглаживаний, даже если они тебе не нравятся" (р<0,05). Обсуждение этих данных представлено в другой работе (Сидоренко Е. В., 1995, с. 65-67).
Решение задачи 8
Вопрос 1: Различаются ли распределения предпочтений, выявленные по каждому из четырех типов мужественности, между собой?
Для выявления различий между четырьмя распределениями лучше всего применить критерий χ2. Критерий λне применим по трем причинам: 1) n<50; 2) разряды представляют собой номинативную шкалу, так как при переходе от типа к типу изменяется "качество", а не "количество" мужественности; 3) критерий λ позволяет сопоставлять только 2 распределения одновременно, а в нашу задачу входит одновременное сопоставление четырех распределений.
Сформулируем гипотезы.
H0: Распределения предпочтений, выявленные по четырем типам мужественности, не различаются между собой.
H1: Распределения предпочтений, выявленные по четырем типам мужественности, различаются между собой.
Рассчитаем теоретические частоты для каждой ячейки таблицы эмпирических частот (Табл. 9.18) по формуле:

fА теор =31-31/124=7.75
fБ теор =31-31/124=7,75 и т. д.
Поскольку суммы по всем строкам и столбцам таблицы равны, теоретические частоты для всех 16-ти ячеек таблицы будут одинаковыми. Равенство же по строкам и столбцам объясняется тем, что каждая испытуемая совершала принужденный выбор, так что каждый из типов мужественности был выбран 31 раз (даже если он был "выбран на последнее место).
Эта задача напоминает шутливый литературный пример, в котором одна невеста совершала выбор из четырех женихов. В данном же случае у нас 31 испытуемая, и каждая совершает выбор из четырех типов мужественности, распределяя их по четырем позициям.
Определим количество степеней свободы V для четырех типов мужественности (k) и четырех позиций выбора (с):
v=(k-l)-(c-l)=(4-l) (4-l)=3·3=9
Все дальнейшие расчеты произведем в таблице по Алгоритму 13 без поправки на непрерывность, так как при v>1 она не требуется.
Таблица 9.18
Расчет критерия χ2при сопоставлении распределений четырех типов мужественности по четырем позициям (n=31)
| Разряды- типы мужественности | Позиции выбора | Эмпирическая частота fэ | Теоретическая частота fт | fэ- fт | (fэ- fт)2 | (fэ- fт)2/ fт |
| 1. Мифологически тип | 7,75 | -5,75 | 33,063 | 4,266 | ||
| 7,75 | -1,75 | 3,063 | 0,395 | |||
| 7,75 | -3,75 | 14,063 | 1,815 | |||
| 7,75 | +11,25 | 126,563 | 16,331 | |||
| 2. Национальный ТИП | 7,75 | +11,25 | 126,563 | 16,331 | ||
| 7,75 | -3,75 | 14,063 | 1,815 | |||
| 7,75 | -0,75 | 0,563 | 0,073 | |||
| 7,75 | -6,75 | 45,563 | 5,879 | |||
| 3, Современный ТИП | 7,75 | -0,75 | 0,563 | 0,073 | ||
| 7,75 | +2,25 | 5,063 | 0,653 | |||
| 7,75 | +4.25 | 18,063 | 2,331 | |||
| 7,75 | -5,75 | 33,063 | 4,266 | |||
| 4, Религиозный ТИП | 7,75 | -4,75 | 22,563 | 2,911 | ||
| 7,75 | +3,25 | 10,563 | 1,362 | |||
| 7,75 | +0,25 | 0,063 | 0,008 | |||
| 7,75 | +1,25 | 1,563 | 0,202 | |||
| Суммы | 124,0 | 58,711 |
По Табл. IX Приложения 1 определяем критические значения χ2 при V=9:

Ответ: H0 отвергается. Принимается H1. Распределения предпочтений по четырем типам мужественности различаются между собой.
Вопрос 2. Можно ли утверждать, что предпочтение отдается какому-то одному или двум типам мужественности? Наблюдается ли какая-либо групповая тенденция предпочтений?
В данном случае удобнее всего применить критерий χ2r Фридмана (см. Главу 3). Как мы помним, он позволяет выявить изменения в величине признака при переходе от одного условия к другому. По-видимому, еще более целесообразным было бы применить тест тенденций L Пейджа, но при n>12 это можно сделать только с помощью специальных ухищрений (см. Задачу 4 и ее решение).
Критерий χ2r позволяет определить, достоверным ли образом различаются суммы рангов, полученные по каждому из рассматриваемых условий, в данном случае - по каждому типу мужественности.
При этом ранги начисляются отдельно по каждому испытуемому, а суммируются - по каждому условию. В нашем случае нет необходимости что-то ранжировать, так как каждая испытуемая своими выборами фактически уже проранжировала четыре исследуемых типа мужественности. Суммы рангов по каждому типу мужественности можно подсчитать, умножая значение ранга на количество рангов с данным значением. Например, из Табл. 9.18 следует, что Мифологический тип 2 раза оказался в первой позиции. Значит, сумма рангов по 1-й позиции будет равна: 1·2=2. На второй позиции он оказался 6 раз, следовательно, сумма рангов по 2-й позиции равна: 2·6=12 и т. д. Произведем расчеты в таблице. Для 3-й позиции Мифологического типа сумма рангов составит 3·4=12, а для 4-й: 4·19=76. Теперь определяем общую сумму рангов Мифологического типа: 2+12+12+76=102.
Таблица 9.19
Расчет ранговых сумм по четырем типам мужественности (n=31) для подсчета критерия χ2r.
| Значение ранга | Типы мужественности | |||||||
| Мифологический | Национальный | Современный | Религиозный | |||||
| faj | faj·rj | faj | faj·rj | faj | faj·rj | faj | faj·rj | |
| Суммы рангов |
Сформулируем гипотезы.
H0: Различия в позициях, которые занимают каждый из четырех типов мужественности, случайны,
H1: Различия в позициях, которые занимают каждый из четырех типов мужественности, неслучайны. Определим эмпирическую величину χ2r по формуле:
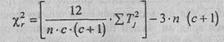
где с - количество условий, в данном случае типов мужественности; п - количество испытуемых; Тj - суммы рангов по каждому из условий.
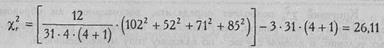
Критические значения определяем по Табл. IX Приложения 1, поскольку при больших п χ2r имеет распределение, сходное с распределением χ2, а существующие таблицы χ2r предназначены только для n≤9.
Количество степеней свободы определим так же, как мы это делали при расчете критерия χ2:
v =( k -l)(c-l)=(4-l) (4~l)=3·3=9
При v=9 критические значения χ2r составляют:
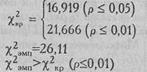
Ответ: Но отвергается. Принимается H1. Различия в позициях, которые занимает каждый из четырех типов мужественности, неслучайны (р<0,01). При этом на первом месте оказывается Национальный тип, на втором - Современный, на третьем - Религиозный и на четвертом - Мифологический тип. На Рис. 9.3. групповая система предпочтений представлена графически.
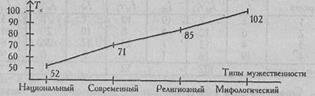
Рис. 9.3. Графики изменения ранговых сумм в последовательности: Национальный тип, Современный тип. Религиозный тип. Мифологический тип; меньшая сумма рангов указывает на большую предпочтительность типа, большая сумма - на меньшую предпочтительность
Итак, различия в ранговых местах каждого из рассматриваемых типов мужественности неслучайны. Наблюдается определенная групповая тенденция предпочтений. Судя по достаточно монотонному повышению кривой на Рис. 9.3, мы вряд ли можем говорить о резком преобладании какого-либо одного из двух типов мужественности. Для статистически достоверного ответа на этот вопрос необходимо сопоставить попарно все типы мужественности по схеме, использованной при решении Задачи 7.
Дата добавления: 2016-06-05; просмотров: 1869;











