Лабораторная работа №15
Тема: Обработка графов в C#. Двойная буферизация графики.
Цель: освоение составления программ с графическим интерфейсом Windows для работы с простыми и ориентированными графами, с реализацией дополнительного буфера для обеспечения плавности анимации.
Теоретические положения
Двойнаябуферизация графики
Для включения двойной буферизации, необходимо при загрузке формы активировать это свойство на самой форме.
private void Form1_Load(object sender, EventArgs e)
{
this.DoubleBuffered = true;
}
При редактировании формы, в Панели элементов нужно добавить на форму объекты PictureBox - поле для рисования и Timer – таймер для обеспечения перерисовки формы.
Для таймера свойство Enabled устанавливается True, а свойство Interval устанавливается 1. Затем если кликнуть два раза по нему, то создастся метод обработки события тика таймера. Добавим в него вызов метода Refresh для перерисовки формы.
private void timer1_Tick(object sender, EventArgs e)
{
Refresh();//перерисовка формы
}
Затем в методе Paint самой формы нужно создать дополнительный буфер с помощью объекта Bitmap.
private void Form1_Paint(object sender, PaintEventArgs e)
{
Bitmap buffer = new Bitmap(Width, Height);//Дополнительный буфер
Graphics gfx = Graphics.FromImage(buffer);//Двойная буферизация
SolidBrush myBrush = new SolidBrush(Color.Black);//кисть
Pen myPen = new Pen(Color.Black);//ручка
gfx.Clear(Color.White);//очистка поверхности
//Здесь можно описать код для отображения того, что необходимо будет анимировать
//Все методы рисования нужно вызывать через gfx – экземпляр объекта Graphics
pictureBox1.Image = buffer;//Двойная буферизация убирает мерцание, так как рисование происходит сначала в буфер, а не напрямую в pictureBox.
myBrush.Dispose();
myPen.Dispose();//Не забыть освободить память от неиспользуемых объектов
}
Таким образом на экране можно будет рисовать не только статичные, но и динамично передвигающиеся элементы с плавной анимацией и без эффекта “мерцания” при смене кадров.
Пример использования данного кода:
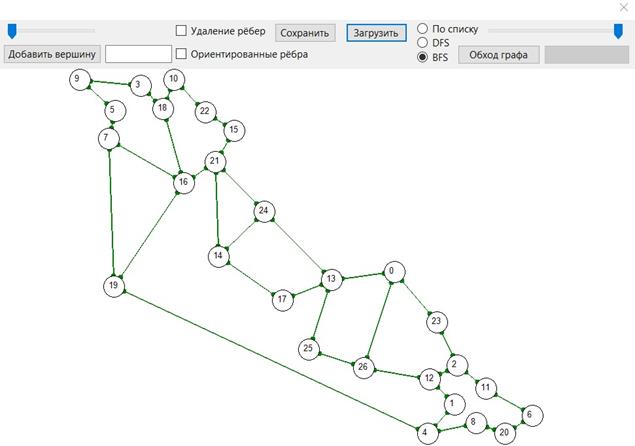
Вершины графа, представленные в этом приложении можно свободно передвигать по области рисования, при этом перемещение происходит плавно и без “мерцания” кадров.
Простой граф
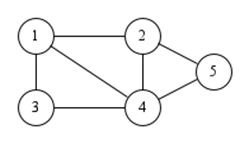
Простой граф (неориентированный граф) G(V,E) состоит из двух множеств. Множество V называется множеством вершин, множество E называется множеством рёбер (E ⊆ V x V). Будем обозначать буквой n количество вершин графа, а буквой m – количество рёбер. Вершины нумеруются числами 1,2 ... n. На рисунке изображён граф с 5 вершинами и 7 рёбрами.
Реализация класса простого графа зависит от выбранного способа представления графа и хранения информации о ребрах. Но в любом случае как минимум необходимо будет внутри класса граф реализовать класс для вершины графа, а затем определить динамический список для экземпляров этого класса. Для работы алгоритмов обработки графа необходимо будет отличать вершины, поэтому в каждой вершине нужно хранить её уникальный идентификатор. Так как в данной работе мы планируем графически отображать граф на экране, стоит заранее позаботиться об координатах отрисовки для каждой вершины, а также другой информации, которая (возможно) понадобится, например, имя вершины.
public class Graph
{
public class Node
{
public int id;//уникальный идентификатор узла
public int x;//координаты
public int y;//для отрисовки вершины
public string name;//отображаемое имя
}
public List<Node> nodes = new List<Node>();//узлы графа
}
Путь в графе
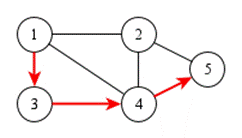
Путь (или маршрут) в графе – это конечная последовательность вершин, в которой каждая вершина (кроме последней) соединена со следующей в последовательности вершиной ребром. Цепью называется маршрут без повторяющихся рёбер. Простой цепью называется маршрут без повторяющихся вершин (откуда следует, что в простой цепи нет повторяющихся рёбер). Путь ведёт из одной вершины в другую и проходит по рёбрам графа. Длиной пути называется количество рёбер в нём. На рисунке показан путь 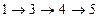 длины 3 из вершины 1 в вершину 5. Циклом называется путь, в котором последняя вершина совпадает с первой. На рисунке изображён цикл
длины 3 из вершины 1 в вершину 5. Циклом называется путь, в котором последняя вершина совпадает с первой. На рисунке изображён цикл 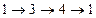 .
.
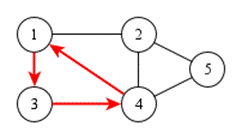
Ориентированный граф
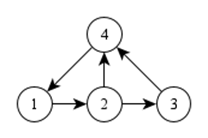
Ориентированный граф G(V,E) по строению схож с простым, однако его множество ребер E имеет два отображения на множество V. Для каждой {v1,v2}, где v1,v2 принадлежат V, v1 – называется начальная вершина, v2 – называется конечная вершина. В ориентированном графе по каждому ребру можно проходить только в одном направлении. На рисунке показан пример ориентированного графа. В нём имеется путь 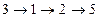 из вершины 3 в вершину 5, но не существует пути из вершины 5 в вершину 3.
из вершины 3 в вершину 5, но не существует пути из вершины 5 в вершину 3.
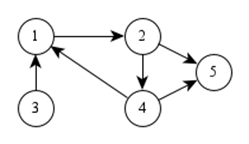
Представление графа
Есть несколько способов представить граф в алгоритмах. Выбор структуры зависит от размера графа и способа его обработки в алгоритме. Далее будут рассмотрены три популярных представления.
Списки смежности
В этом случае каждой вершине x сопоставляется список смежности, включающий вершины, соединённые с x вершиной. Список смежности – самый популярный способ представления графов, они позволяют эффективно реализовать большинство алгоритмов.
Списки смежности удобно хранить в массиве списков, который объявлен следующим образом:
List<int>[] g = new List<int>[n];
Граф на рисунке можно сохранить так:
g[0].Add(1);
g[1].Add(2);
g[1].Add(3);
g[2].Add(3);
g[3].Add(0);
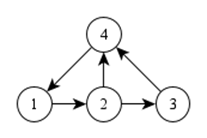
Неориентированные графы можно хранить аналогично, только каждое ребро нужно учитывать в двух списках смежности (для обоих направлений).
Для взвешенных графов структуру следует дополнить:
List<Pair<int>>[] g = new List<Pair<int>>[n];
В этом случае список смежности вершины 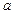 содержит пару
содержит пару 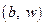 , если существует ребро с весом
, если существует ребро с весом 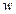 , направленное от
, направленное от 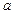 к
к 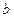 .
.
Списки смежности позволяют эффективно находить вершины, в которые можно перейти из данной по одному ребру. Следующий цикл обходит все вершины, в которые можно попасть из вершины 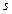 :
:
foreach (int u in g[s]) {
// обработать вершину u
}
Матрица смежности
Матрица смежности показывает, какие рёбра есть в графе. С её помощью можно эффективно проверить, существует ли ребро между двумя вершинами. Матрицу можно хранить в виде массива
int[,] g = new int[n, n];
где элемент 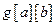 равен 1, если существует ребро, ведущее из вершины
равен 1, если существует ребро, ведущее из вершины 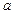 в вершину
в вершину 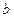 , а в противном случае равен 0.
, а в противном случае равен 0.
Так, матрица смежности для графа на рисунке имеет вид
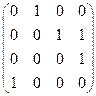
Если граф взвешенный, то представление в виде матрицы смежности можно обобщить: если две вершины соединены ребром, то в матрице хранится вес этого ребра.
Так, граф на рисунке представляется следующей матрицей:
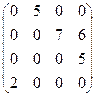
Недостаток матрицы смежности заключается в том, что она содержит 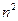 элементов, большая часть которых обычно равна 0. Поэтому такое представление не годится для больших графов.
элементов, большая часть которых обычно равна 0. Поэтому такое представление не годится для больших графов.
Список рёбер
Список рёбер содержит все рёбра графа в некотором порядке. Это представление удобно, если алгоритм обрабатывает все рёбра и не требуется находить рёбра, начинающиеся в заданной вершине.
Список рёбер можно хранить в списке
List<Pair<int>> g = new List<Pair<int>>();
где наличие пары 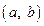 означает, что существует ребро из вершины
означает, что существует ребро из вершины 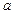 в вершину
в вершину 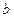 .
.
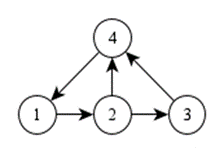
Граф на рисунке можно представить следующим образом:
g.Add(new Pair<int>(0, 1));
g.Add(new Pair<int>(1, 2));
g.Add(new Pair<int>(1, 3));
g.Add(new Pair<int>(2, 3));
g.Add(new Pair<int>(3, 0));
Для взвешенных графов структуру можно обобщить:
List<Triple<int>> g = new List<Triple<int>>();
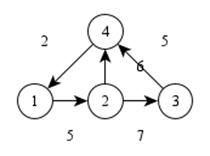
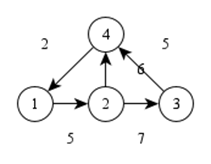
Например, граф на рисунке можно представить следующим образом:
g.Add(new Triple<int>(0, 1, 4));
g.Add(new Triple<int>(1, 2, 6));
g.Add(new Triple<int>(1, 3, 5));
g.Add(new Triple<int>(2, 3, 4));
g.Add(new Triple<int>(3, 0, 1));
Дополнительные характеристики графов
Граф называется:
1) связным, если для любых вершин u, v есть путь из u в v.
2) сильно связным или ориентированно связным, если он ориентированный, и из любой вершины в любую другую имеется ориентированный путь.
3) деревом, если он связный и не содержит нетривиальных циклов.
4) полным, если любые его две (различные, если не допускаются петли) вершины соединены ребром.
Обход графа
Поиск в глубину
Поиск в глубину (depth-first search – DFS) – прямолинейный способ обхода графа. Алгоритм начинает работу в начальной вершине и перебирает все вершины, достижимые из неё по рёбрам графа.
Поиск в глубину всегда следует по одному пути, пока на нём ещё имеются вершины. После этого он возвращается назад и начинает исследовать другие части графа. Алгоритм запоминает посещённые вершины, так что каждая обрабатывается только один раз.
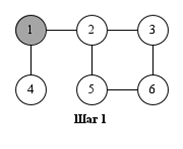
На рисунке показан порядок обработки вершин при поиске в глубину.
Поиск может начинаться с любой вершины: в данном случае – с вершины 1.
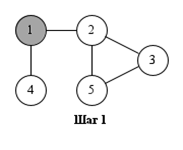
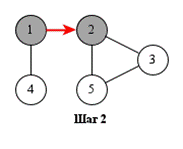
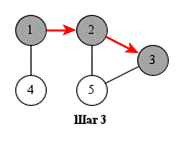
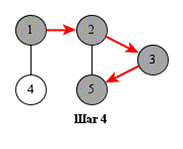
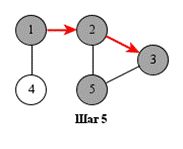
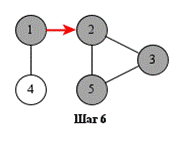
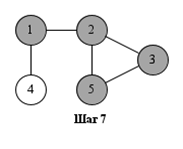
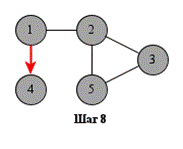
Поиск в глубину удобно реализовать рекурсивно. Показанная ниже функция dfs начинает поиск с заданной вершины. Предполагается, что граф представлен списками смежности, хранящимися в массиве
List<int>[] g = new List<int>[n];
Кроме того, используется массив
bool[] used = new bool[n];
в котором запоминаются посещенные вершины. В начальный момент все элементы этого массива равны 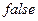 , но когда алгоритм заходит в вершину
, но когда алгоритм заходит в вершину 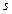 , в элемент
, в элемент 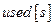 записывается
записывается 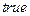 .
.
Функцию можно реализовать следующим образом:
void dfs(int s)
{
if (used[s]) return;
used[s] = true;
// обработать вершину s
foreach (int u in g[s])
dfs(u);
}
Временная сложность поиска в глубину равна 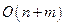 , где
, где 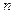 – число вершин, а
– число вершин, а 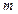 – число рёбер, поскольку алгоритм обрабатывает каждую вершину и каждое ребро ровно один раз.
– число рёбер, поскольку алгоритм обрабатывает каждую вершину и каждое ребро ровно один раз.
Поиск в ширину
При поиске в ширину (breadth-first search – BFS) вершины графа посещаются в порядке возрастания расстояния от начальной вершины. Следовательно, используя поиск в ширину, можно будет вычислить расстояния от начальной вершины до всех остальных. Однако реализовать поиск в ширину труднее, чем поиск в глубину.
В процессе поиска в ширину вершины обходятся уровень за уровнем. Сначала посещаются вершины, отстоящие от начальной на расстояние 1, затем – на расстояние 2 и т. д. Процесс продолжается, пока не останется непосещённых вершин.
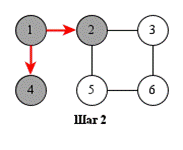
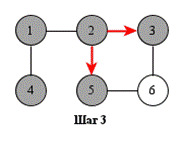
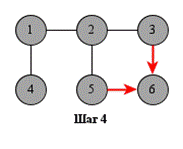
Поиск в ширину труднее реализовать, чем поиск в глубину, потому что алгоритм посещает вершины, находящиеся в разных частях графа. Типичная реализация основана на очереди вершин. На каждом шаге обрабатывается следующий узел из очереди.
Предполагается, что граф представлен списками смежности и что определены следующие структуры данных:
Queue<int> q = new Queue<int>();
bool[] used = new bool[n];
int[] d = new int[n];
Очередь 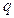 содержит вершины, подлежащие обработке в порядке возрастания расстояния. Новые вершины добавляются в конец очереди, а обрабатывается вершина, находящаяся в начале очереди. В массиве
содержит вершины, подлежащие обработке в порядке возрастания расстояния. Новые вершины добавляются в конец очереди, а обрабатывается вершина, находящаяся в начале очереди. В массиве 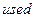 хранится информация о том, какие вершины уже посещались, а в массиве
хранится информация о том, какие вершины уже посещались, а в массиве 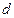 – расстояния от начальной вершины до всех остальных вершин графа.
– расстояния от начальной вершины до всех остальных вершин графа.
Поиск, начинающийся в вершине 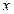 , реализуется следующим образом:
, реализуется следующим образом:
used[x] = true;
d[x] = 0;
q.Enqueue(x);
while (q.Count > 0)
{
int s = q.Peek(); q.Dequeue();
// обработать вершину s
foreach (int u in g[s])
{
if (used[u]) continue;
used[u] = true;
d[u] = d[s] + 1;
q.Enqueue(u);
}
}
Временная сложность поиска в ширину, как и поиска в глубину, равна 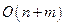 , где
, где 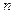 – число вершин, а
– число вершин, а 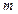 – число ребер.
– число ребер.
Стенд с примером реализации приложения с графическим интерфейсом, в котором есть анимированные методы обхода графов DFS и BFS: https://github.com/Mistral-war2ru/Graph.
Задание
1. Написать программную реализацию класса графа с возможностью добавления элементов во множество вершин и во множество ребер. Способ представления ребер зависит от варианта индивидуальной задачи (списки смежности, матрица смежности, список ребер). Реализовать графический интерфейс с двойной буферизацией, в котором элементы графа можно свободно перемещать по области рисования.
2. Разработать метод класса для обработки данных графа согласно индивидуальному заданию из табл. 16. Результат обработки отражать графически и выводить посредством элементов управления TextBox согласно индивидуальному заданию из табл. 16.
3. Операции загрузки, сохранения и обработки графа инициировать посредством элементов управления Button.
4. Разработать модульный тест для метода обработки графа. При проверке читать граф из файла G.grf.
5. При программировании задачи выполнять обработку исключительных ситуаций.
6. Представить результаты выполнения программы и сделать выводы по работе.
Таблица 16. Варианты индивидуальных заданий к лабораторной работе №15
| № вар. | Задание | Вид* графа | Способ представления | Метод обхода |
| Топологическая сортировка. Вывести последовательно названия вершин в TextBox через запятую. | Н | Списки смежности | DFS | |
| Найдите степени всех вершин графа. Графически рядом с каждой вершиной вывести на картинке число – степень этой вершины. | Н | Список ребер | Любой | |
| Нахождение кратчайших путей. Обеспечить возможность пользователю выбрать две вершины (кликами мышки либо вводом названий в TextBox). Графически отобразить путь из первой во вторую, если он есть, иначе вывести в TextBox, что путь не существует. | Н | Любой | Алгоритм Дейкстры | |
| Поиск всех вершин графа, которые являются истоками, и всех вершин графа, которые являются стоками. Графически отобразить истоки синим цветом, а стоки красным. Либо вывести в TextBox, что таких вершин в графе нет. | О | Матрица смежности | Любой | |
| Нахождение отрицательного цикла в графе Графически отобразить вершины, входящие в найденный цикл красным цветом, либо вывести в TextBox, что цикл не найден. | Н | Списки смежности | Любой | |
| Проверить является ли граф регулярным. Вывести в TextBox результат проверки как NO или YES. | О | Списки смежности | Реализовать и сравнить DFS и BFS. | |
| Поиск мостов. Графически отобразить найденные вершины синим цветом, либо вывести в TextBox сообщение о том, что таких вершин нет. | Н | Любой | DFS | |
| Нахождение эйлеровых путей. Графически отобразить начальную вершину желтым, а конечную фиолетовым, если они совпали, то коричневым. Либо вывести в TextBox, что такого пути не существует. | Н | Матрица смежности | Любой | |
| Нахождение эйлеровых циклов. Графически отобразить первое ребро из цикла красным, второе и далее синим, последнее оранжевым. Либо вывести в TextBox, что такого цикла не существует. | О | Списки смежности | Любой | |
| Нахождение параллельных (кратных) ребер. Обеспечить возможность добавления большего количества ребер между двумя одинаковыми вершинами (убрать проверку на совпадения при добавлении нового). Графически отобразить коричневым ребра с кратностью больше 1. Вывести в TextBox максимальную кратность среди всех ребер. | О | Список ребер | Любой | |
| Построение минимального остовного дерева Графически отобразить синим цветом ребра, принадлежащие дереву. Вывести в TextBox количество ребер, оставшихся в дереве. | Н | Любой | Алгоритм Краскала | |
| Нахождение компонент сильной связности. Графически отобразить вершины для каждого компонента разными цветами (использовать Random). Вывести в TextBox количество таких компонентов. | О | Любой | Алгоритм Косарайю | |
| Поиск точек сочленения Графически отобразить эти вершины красным цветом, либо вывести в TextBox, что таких вершин нет. | О | Любой | DFS | |
| Проверить является ли граф деревом. Вывести в TextBox результат YES или NO. | Н | Матрица смежности | Реализовать и сравнить DFS и BFS. | |
| Раскраска двудольного графа. Графически отобразить красные и синие вершины. | Н | Любой | BFS | |
| Нахождение кратчайшего цикла. Графически отобразить вершины из найденного цикла оранжевым цветом. Либо вывести в TextBox, что в графе нет циклов. | О | Любой | BFS | |
| Нахождение гамильтоновых путей. Графически отобразить ребра фиолетовым цветом. Вывести в TextBox длину пути. | Н | Матрица смежности | Любой | |
| Нахождение гамильтоновых циклов. Графически отобразить ребра серым цветом. Либо вывести в TextBox, что такого цикла не существует. | О | Списки смежности | Любой | |
| Нахождение компонентов связности. Графически отобразить вершины для каждого компонента разными цветами (использовать Random). Вывести в TextBox количество таких компонентов. | О | Список ребер | Любой | |
| Нахождение кратчайших путей. Обеспечить возможность пользователю выбрать две вершины (кликами мышки либо вводом названий в TextBox). Графически отобразить путь из первой во вторую, если он есть, иначе вывести в TextBox, что путь не существует. | Н | Любой | Алгоритм Флойда-Уоршелла |
* Н – Неориентированный, О – Ориентированный
Контрольные вопросы.
1. Что такое простой граф? Что такое ориентированный граф?
2. Что такое путь в графе?
3. Способы представления графа в памяти средствами языка С#.
4. Использование поиска в глубину для обхода графа.
5. Использование поиска в ширину для обхода графа.
6. Свойства объекта Timer.
7. Как вызвать перерисовку формы?
8. Как создать и использовать двойной буфер для графики?
9. Что такое взвешенный граф?
10. Дополнительные свойства графов: связность, полнота, вершина исток, вершина сток, компоненты связности, степень вершины.
Дата добавления: 2021-12-14; просмотров: 650;











