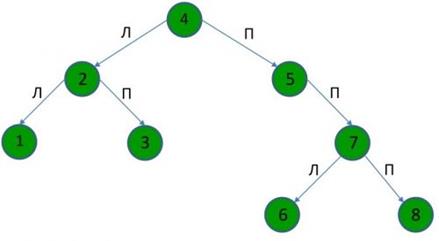
Симметричный порядок
Порядок следования при обратном обходе дерева: 1, 2, 3, 4, 5, 6, 7, 8
Задание
1. Дана последовательность целых чисел, оканчивающаяся нулем. Написать программную реализацию класса для внесения и хранения данной последовательности в виде дерева двоичного поиска. Реализовать графический интерфейс.
2. Разработать два метода обработки данных исходного дерева согласно индивидуальному заданию из табл. 15. Преобразованное дерево сохранить в файл tree.res. После преобразования проверить, осталось ли дерево деревом двоичного поиска. Результат этой проверки, а также число, возвращенное методом вычисления показателя, выводить посредством элементов управления TextBox.
3. Операции построения и обработки дерева инициировать посредством элементов управления CommandButton.
4. Для прорисовки исходного и результатного бинарного дерева использовать элементы управления PictureBox. Использовать классы Graphics, Pen и Brush пространства имен System.Drawing.
5. Рассчитанные скалярные значения выводить посредством элемента управления TextBox.
6. Разработать модульный тест для метода преобразования дерева. При проверке читать дерево из файла tree.res.
7. При программировании задачи выполнять обработку исключительных ситуаций.
8. Представить результаты выполнения программы и сделать выводы по работе.
Таблица 15. Варианты индивидуальных заданий к лабораторной работе №10
| № вар. | Задание на преобразование дерева | Задание на вычисление показателя |
| Обнулить все совершенные листья дерева, большие разности максимального и минимального значения элементов дерева | Найти сумму элементов, расположенных на максимальном уровне от корня | |
| Поменять знак элементов дерева, меньших среднего арифметического листьев дерева | Найти разность суммы элементов, расположенных на четных уровнях, и суммы элементов – на нечетных уровнях дерева | |
| Все отрицательные элементы дерева заменить их квадратами | Найти сумму элементов на каждом уровне дерева | |
| Обнулить листья дерева с нечетным количеством цифр | Найти уровень с максимальной суммой элементов | |
| Если в дереве встречаются числа Фибоначчи, то все отрицательные элементы заменить их модулем | Найти уровень с максимальным количеством листьев | |
| Даны два дерева двоичного поиска. Все простые элементы второго дерева добавить в первое | Найти уровень, элементы которого наименее отличаются от среднего арифметического значения этого уровня | |
| Обнулить узлы, имеющие ровно два потомка со значениями разного знака | Найти уровень с максимальным количеством простых элементов | |
| Обнулить узлы, имеющие потомка с простым значением | Найти среднее значение элементов для каждого уровня бинарного дерева | |
| Заменить значения простых элементов дерева максимальным значением всех простых листьев дерева | Найти сумму левых элементов нечетных уровней дерева | |
| Удалить все листья дерева, являющиеся правыми потомками | Найти уровень, на котором больше всего узлов с двумя потомками | |
| Удалить все листья дерева, являющиеся левыми потомками | Найти количество уровней дерева, на которых встречаются отрицательные элементы | |
| Поменять местами корень дерева и элемент, наиболее близкий к среднему арифметическому элементов дерева | Найти номера двух уровней бинарного дерева, сумма элементов которых максимальна | |
| Поменять местами элементы с максимальным и минимальным значением | Найти номер уровня бинарного дерева с максимальной суммой элементов | |
| Обнулить элементы, являющиеся совершенным числом и среди потомков которых также есть совершенные числа | Найти наибольший элемент дерева из числа правых элементов | |
| Обнулить элементы дерева, потомки которых являются числами Фибоначчи | Найти уровень бинарного дерева с одинаковым количеством положительных и отрицательных элементов | |
| Заменить четные элементы дерева нулём | Найти наименьший четный элемент среди ветвей дерева | |
| Удвоить значение каждой положительной вершины дерева | Найти среднее арифметическое всех листьев дерева | |
| Поменять знак каждой ветви дерева с нечетным значением | Определить глубину заданного элемента дерева, равного заданному значению n, либо возвратить –1, если такого элемента нет | |
| Даны два дерева двоичного поиска. Все совершенные элементы второго дерева добавить в первое | По заданному числу n определить количество всех вершин, находящихся на уровне с номером n в дереве. | |
| Даны два дерева двоичного поиска. Построить дерево двоичного поиска, содержащее все простые элементы двух деревьев. | Найти количество вершин дерева, значение которых не кратно заданному числу n |
Дата добавления: 2021-12-14; просмотров: 393;
Поиск по сайту
Узнать еще
- II. Види виробничої документації та порядок її ведення
- II. Порядок разработки, утверждения, внесения изменений в Инструкцию по делопроизводству
- III. Порядок присвоения спортивных званий
- IV. Движение поездов при неисправности электрожезловой системы и порядок регулировки количества жезлов в жезловых аппаратах
- IV. Порядок выполнения работы
- IV. Порядок присвоения спортивных разрядов
- V. Порядок лишения, восстановления спортивных званий
- VI. Порядок лишения, восстановления спортивных разрядов
Публикации по технике и механике
Публикации по биологии
Публикации по информатике
Публикации по строительству
Публикации по физике
Публикации по химии
Публикации по электронике
Публикации по искусству
Публикации по истории
Публикации по медицине
