Принятие решения о задаче и методе обработки на стадии, когда данные уже получены

1. По первому столбцу Табл. 1.2 определить, какая из задач стоит в вашем исследовании.

2. По второму столбцу Табл. 1.2 определить, каковы условия решения вашей задачи, например, сколько выборок обследовано или на какое количество групп вы можете разделить обследованную выборку.

3. Обратиться к соответствующей главе и по алгоритму принятия решения о выборе критерия, приведенного в конце каждой главы, определить, какой именно метод или критерий вам целесообразно использовать.

Если вы еще находитесь на стадии планирования исследования, то лучшее заранее подобрать математическую модель, которую вы бу­дете в дальнейшем использовать. Особенно необходимо планирование в тех случаях, когда в перспективе предполагается использование крите­риев тенденций или (в еще большей степени) дисперсионного анализа. , В этом случае алгоритм принятия решения таков:

АЛГОРИТМ 2

Принятие решения о задаче и методе обработки на стадии планирования исследования

1. Определите, какая модель вам кажется наиболее подходящей для доказательства] ваших научных предположений.

2. Внимательно ознакомьтесь с описанием метода, примерами и задачами для самостоятельного решения, которые к нему прилагаются.

3. Если вы убедились, что это то, что вам нужно, вернитесь к разделу "Ограничения критерия" и решите, сможете ли вы собрать данные, которые будут отвечать этим ограничениям (большие объемы выборок, наличие не­скольких выборок, монотонно различающихся по какому-либо признаку, напри­мер, по возрасту и т.п.).

4. Проводите исследование, а затем обрабатывайте полученные данные по заранее! выбранному алгоритму, если вам удалось выполнить ограничения.

5. Если ограничения выполнить не удалось, обратитесь к алгоритму 1.

В описании каждого критерия сохраняется следующая последова­тельность изложения:

· назначение критерия;

· описание критерия;

· гипотезы, которые он позволяет проверить;

· графическое представление критерия;

· ограничения критерия;

· пример или примеры.

Кроме того, для каждого критерия создан алгоритм расчетов. Ес­ли критерий сразу удобнее рассчитывать по алгоритму, то он приводит­ся в разделе "Пример"; если алгоритм легче можно воспринять уже после рассмотрения примера, то он приводится в конце параграфа, со­ответствующего данному критерию.

Список обозначений

Латинские обозначения:

А - показатель асимметрии распределения

с - количество групп или условий измерения

d - разность между рангами, частотами или частостями

df - число степеней свободы в дисперсионном анализе

Е - показатель эксцесса

F - критерий Фишера для сравнения дисперсий

f - частота

f* - частость, или относительная частота

G - критерий знаков

Н - критерий Крускала-Уоллиса

i - индекс, обозначающий порядковый номер наблюдения

j - индекс, обозначающий порядковый номер разряда, класса, группы

k - количество классов или разрядов признака

L - критерий тенденций Пейджа

М - среднее значение признака или средняя арифметическая; то же, что и ^х

m - биномиальный критерий

n - количество наблюдений (испытуемых, реакций, выборов и т.п.)

N - общее количество наблюдений в двух или более выборках

Р - вероятность того, что событие произойдет

р - вероятность ошибки 1 рода (то же, что и а), уровень статисти­ческой значимости

Q - 1) вероятность того, что событие не произойдет; 2) критерий Розенбаума

r_s - коэффициент ранговой корреляции Спирмена

S - критерий Джонкира

S² - оценка дисперсии

S_i - количество значений, которые выше или ниже данного значения

SS - суммы квадратов (в дисперсионном анализе)

Т - критерий Вилкоксона

Т_с - суммы рангов по столбцам

Т_к - большая сумма рангов в критерии U

U - критерий Манна-Уитни

Wn - размах вариативности, или диапазон значений от наименьшего до

наибольшего

х_i - текущее наблюдение; каждое наблюдение по порядку

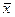- среднее значение признака (то же, что и М)

Греческие обозначения:

α(альфа) - вероятность ошибки I рода (отклонения H₀, которая верна)

β (бета) - вероятность ошибки II рода (принятия H₀, которая неверна)

λ, (ламбда) - критерий Колмогорова-Смирнова

v (ню) - число степеней свободы в непараметрических критериях

σ (сигма) - стандартное отклонение

φ (фи) - центральный угол, определяемый по процентной доле в критерии φ*

φ* (фи) - критерий Фишера с угловым преобразованием

χ² (хи-квадрат) - критерий Пирсона

χ²_r (хи-ар-квадрат) - критерий Фридмана.

ГЛАВА 2