Распределение признака. Параметры распределения

ОСНОВНЫЕ ПОНЯТИЯ, ИСПОЛЬЗУЕМЫЕ

В МАТЕМАТИЧЕСКОЙ ОБРАБОТКЕ

ПСИХОЛОГИЧЕСКИХ ДАННЫХ

Признаки и переменные

Признаки и переменные - это измеряемые психологические явле­ния. Такими явлениями могут быть время решения задачи, количество допущенных ошибок, уровень тревожности, показатель интеллектуаль­ной лабильности, интенсивность агрессивных реакций, угол поворота корпуса в беседе, показатель социометрического статуса и множество других переменных.

Понятия признака и переменной могут использоваться как взаи­мозаменяемые. Они являются наиболее общими. Иногда вместо них используются понятия показателя или уровня, например, уровень на­стойчивости, показатель вербального интеллекта и др. Понятия показа­теля и уровня указывают на то, что признак может быть измерен коли­чественно, так как к ним применимы определения "высокий" или "низкий", например, высокий уровень интеллекта, низкие показатели тревожности и др.

Психологические переменные являются случайными величинами, поскольку заранее неизвестно, какое именно значение они примут.

Математическая обработка - это оперирование со значениями признака, полученными у испытуемых в психологическом исследовании. Такие индивидуальные результаты называют также "наблюдениями", "наблюдаемыми значениями", "вариантами", "датами", "индивидуальны­ми показателями" и др. В психологии чаще всего используются терми­ны "наблюдение" или "наблюдаемое значение".

Значения признака определяются при помощи специальных шкал измерения.

Шкалы измерения

Измерение - это приписывание числовых форм объектам или собы­тиям в соответствии с определенными правилами (Стивене С, 1960, с.60). С.Стивенсом предложена классификация из 4 типов шкал измерения:

1) номинативная, или номинальная, или шкала наименований;

2) порядковая, или ординальная, шкала;

3) интервальная, или шкала равных интервалов;

4) шкала равных отношений.

Номинативная шкала- это шкала, классифицирующая по назва­нию: потеп (лат.) - имя, название. Название же не измеряется количе­ственно, оно лишь позволяет отличить один объект от другого или од­ного субъекта от другого. Номинативная шкала - это способ классифи­кации объектов или субъектов, распределения их по ячейкам классифи­кации.

Простейший случай номинативной шкалы - дихотомическая шка­ла, состоящая всего лишь из двух ячеек, например: "имеет братьев и сестер - единственный ребенок в семье"; "иностранец - соотечествен­ник"; "проголосовал "за" - проголосовал "против"" и т.п.

Признак, который измеряется по дихотомической шкале наимено­ваний, называется альтернативным. Он может принимать всего два значения. При этом исследователь зачастую заинтересован в одном из них, и тогда он говорит, что признак “проявился”, если тот принял ин­тересующее его значение, и что признак “не проявился” , если он при­нял противоположное значение. Например: "Признак леворукости про­явился у 8 испытуемых из 20". В принципе номинативная шкала может состоять из ячеек "признак проявился - признак не проявился .

Более сложный вариант номинативной шкалы - классификация из трех и более ячеек, например: "экстрапунитивные - интрапунитивные -импунитивные реакции" или "выбор кандидатуры А - кандидатуры Б -кандидатуры В - кандидатуры Г" или "старший - средний - младший -единственный ребенок в семье" и др.

Расклассифицировав все объекты, реакции или всех испытуемых по ячейкам классификации, мы получаем возможность от наименований перейти к числам, подсчитав количество наблюдений в каждой из ячеек.

Как уже указывалось, наблюдение - это одна зарегистрированная реакция, один совершенный выбор, одно осуществленное действие или результат одного испытуемого.

Допустим, мы определим, что кандидатуру А выбрали 7 испы­туемых, кандидатуру Б - 11, кандидатуру В - 28, а кандидатуру Г -всего 1. Теперь мы можем оперировать этими числами, представляю­щими собой частоты встречаемости разных наименований, то есть час­тоты принятия признаком "выбор" каждого из 4 возможных значений. Далее мы можем сопоставить полученное распределение частот с рав­номерным или каким-то иным распределением.

Таким образом, номинативная шкала позволяет нам подсчитывать частоты встречаемости разных "наименований", или значений признака, и затем работать с этими частотами с помощью математических методов.

Единица измерения, которой мы при этом оперируем - количест­во наблюдений (испытуемых, реакций, выборов и т. п.), или частота. Точнее, единица измерения - это одно наблюдение. Такие данные могут быть обработаны с помощью метода χ², биномиального критерия m и углового преобразования Фишера φ*.

Порядковая шкала- это шкала, классифицирующая по принци­пу "больше - меньше". Если в шкале наименований было безразлично, в каком порядке мы расположим классификационные ячейки, то в по­рядковой шкале они образуют последовательность от ячейки "самое ма­лое значение" к ячейке "самое большое значение" (или наоборот). Ячейки теперь уместнее называть классами, поскольку по отношению к классам употребимы определения "низкий", "средний" и "высокий" класс, или 1-й, 2-й, 3-й класс, и т.д.

В порядковой шкале должно быть не менее трех классов, напри­мер "положительная реакция - нейтральная реакция - отрицательная реакция" или "подходит для занятия вакантной должности - подходит с оговорками - не подходит" и т. п.

В порядковой шкале мы не знаем истинного расстояния между классами, а знаем лишь, что они образуют последовательность. Напри­мер, классы "подходит для занятия вакантной должности" и "подходит с оговорками" могут быть реально ближе друг к другу, чем класс "подходит с оговорками" к классу "не подходит".

От классов легко перейти к числам, если мы условимся считать, что низший класс получает ранг 1, средний класс - ранг 2, а высший класс - ранг 3, или наоборот. Чем больше классов в шкале, тем больше у нас возможностей для математической обработки полученных данных и проверки статистических гипотез.

Например, мы можем оценить различия между двумя выборками испытуемых по преобладанию у них более высоких или более низких рангов или подсчитать коэффициент ранговой корреляции между двумя переменными, измеренными в порядковой шкале, допустим, между оценками профессиональной компетентности руководителя, данными ему разными экспертами.

Все психологические методы, использующие ранжирование, по­строены на применении шкалы порядка. Если испытуемому предлагает­ся упорядочить 18 ценностей по степени их значимости для него, проранжировать список личностных качеств социального работника или 10 претендентов на эту должность по степени их профессиональной при­годности, то во всех этих случаях испытуемый совершает так называе­мое принудительное ранжирование, при котором количество рангов со­ответствует количеству ранжируемых субъектов или объектов (ценностей, качеств и т.п.).

Независимо от того, приписываем ли мы каждому качеству или испытуемому один из 3-4 рангов или совершаем процедуру принуди­тельного ранжирования, мы получаем в обоих случаях ряды значений, измеренные по порядковой шкале. Правда, если у нас всего 3 возмож­ных класса и, следовательно, 3 ранга, и при этом, скажем, 20 ранжи­руемых испытуемых, то некоторые из них неизбежно получат одинако­вые ранги. Все многообразие жизни не может уместиться в 3 градации, поэтому в один и тот же класс могут попасть люди, достаточно серьез­но различающиеся между собой. С другой стороны, принудительное ранжирование, то есть образование последовательности из многих ис­пытуемых, может искусственно преувеличивать различия между людь­ми. Кроме того, данные, полученные в разных группах, могут оказаться несопоставимыми, так как группы могут изначально различаться по уровню развития исследуемого качества, и испытуемый, получивший в одной группе высший ранг, в другой получил бы всего лишь средний, и т.п.

Выход из положения может быть найден, если задавать доста­точно дробную классификационную систему, скажем, из 10 классов, или градаций, признака. В сущности, подавляющее большинство психологи­ческих методик, использующих экспертную оценку, построено на изме­рении одним и тем же "аршином" из 10, 20 или даже 100 градаций разных испытуемых в разных выборках.

Итак, единица измерения в шкале порядка - расстояние в 1 класс или в 1 ранг, при этом расстояние между классами и рангами может быть разным (оно нам неизвестно). К данным, полученным по поряд­ковой шкале, применимы все описанные в данной книге критерии и ме­тоды.

Интервальная шкала- это шкала, классифицирующая по прин­ципу "больше на определенное количество единиц - меньше на опреде­ленное количество единиц". Каждое из возможных значений признака отстоит от другого на равном расстоянии.

Можно предположить, что если мы измеряем время решения за­дачи в секундах, то это уже явно шкала интервалов. Однако на самом деле это не так, поскольку психологически различие в 20 секунд между испытуемым А и Б может быть отнюдь не равно различию в 20 се­кунд между испытуемыми Б и Г, если испытуемый А решил задачу за 2 секунды, Б - за 22, В - за 222, а Г - за 242.

Аналогичным образом, каждая секунда после истечения полутора минут в опыте с измерением мышечного волевого усилия на динамомет­ре с подвижной стрелкой, по "цене", может быть, равна 10 или даже более секундам в первые полминуты опыта. "Одна секунда за год идет" - так сформулировал это однажды один испытуемый.

Попытки измерять психологические явления в физических едини­цах - волю в секундах, способности в сантиметрах, а ощущение собст­венной недостаточности - в миллиметрах и т. п., конечно, понятны, ведь все-таки это измерения в единицах "объективно" существующего времени и пространства. Однако ни один опытный исследователь при этом не обольщает себя мыслью, что он совершает измерения по психо­логической интервальной шкале. Эти измерения принадлежат по-прежнему к шкале порядка, нравится нам это или нет (Стивене С, 1960, с.56; Паповян С.С., 1983, с.63; Михеев В.И.: 1986, с.28).

Мы можем с определенной долей уверенности утверждать лишь, что испытуемый А решил задачу быстрее Б, Б быстрее В, а В быстрее Г.

Аналогичным образом, значения, полученные испытуемыми в баллах по любой нестандартизованной методике, оказываются измерен­ными лишь по шкале порядка. На самом деле равноинтервальными можно считать лишь шкалы в единицах стандартного отклонения и про-центильные шкалы, и то лишь при условии, что распределение значений в стандартизующей выборке было нормальным (Бурлачук Л. Ф., Мо­розов С. М., 1989, с. 163, с. 101).

Принцип построения большинства интервальных шкал построен на известном правиле "трех сигм": примерно 97,7-97,8% всех значений признака при нормальном его распределении укладываются в диапазоне М±3σ[1] Можно построить шкалу в единицах долей стандартного откло­нения, которая будет охватывать весь возможный диапазон изменения признака, если крайний слева и крайний справа интервалы оставить открытыми.

Р.Б. Кеттелл предложил, например, шкалу стенов - "стандартной десятки". Среднее арифметическое значение в "сырых" баллах прини­мается за точку отсчета. Вправо и влево отмеряются интервалы, равные 1/2 стандартного отклонения. На Рис. 1.2 представлена схема вычисле­ния стандартных оценок и перевода "сырых" баллов в стены по шкале N 16-факторного личностного опросника Р. Б. Кеттелла.

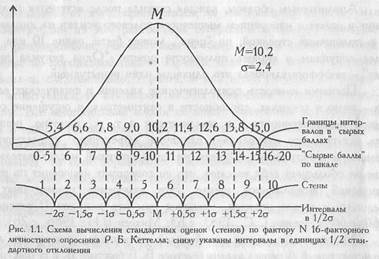
Справа от среднего значения будут располагаться интервалы, равные 6, 7, 8, 9 и 10 стенам, причем последний из этих интервалов открыт. Слева от среднего значе­ния будут располагаться интервалы, равные 5, 4, 3, 2 и 1 стенам, и крайний интервал также открыт. Теперь мы поднимаемся вверх, к оси "сырых баллов", и размечаем границы интервалов в единицах "сырых" баллов. Поскольку М=10,2; σ=2,4, вправо мы откладываем 1/2σ, т.е. 1,2 "сырых" балла. Таким образом, гра­ница интервала составит: (10,2 + 1,2) = 11,4 "сырых" балла. Итак, границы ин­тервала, соответствующего 6 стенам, будут простираться от 10,2 до 11,4 баллов. В сущности, в него попадает только одно "сырое" значение - 11 баллов. Влево от средней мы откладываем 1/2 σ и получаем границу интервала: 10,2-1,2=9. Таким образом, границы интервала, соответствующие 9 стенам, простираются от 9 до 10,2. В этот интервал попадают уже два "сырых" значения - 9 и 10. Если испы­туемый получил 9 "сырых" баллов, ему начисляется теперь 5 стенов; если он по­лучил 11 "сырых" баллов - 6 стенов, и т. д.

Мы видим, что в шкале стенов иногда за разное количество "сырых" баллов будет начисляться одинаковое количество стенов. Например, за 16, 17, 18, 19 и 20 баллов будет начисляться 10 стенов, а за 14 и 15 - 9 стенов и т. д.

В принципе,шкалу стенов можно построить по любым данным, измеренным по крайней мере в порядковой шкале, при объеме выборки п>200 и нормальном рас­пределении признака[2].

Другой способ построения равноинтервальной шкалы - группировка интервалов по принципу равенства накопленных частот. При нормальном распределении при­знака в окрестности среднего значения группируется большая часть всех наблюде­ний, поэтому в этой области среднего значения интервалы оказываются меньше, уже, а по мере удаления от центра распределения они увеличиваются, (см. Рис. 1.2). Следовательно, такая процентильная шкала является равноинтервальной толь­ко относительно накопленной частоты (Мельников В.М., Ямпольский Л.Т., 1985, с. 194).

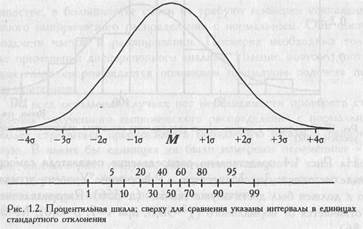
Построение шкал равных интервалов по данным, полученным по шкале порядка, напоминает трюк с веревочной лестницей, на который ссылался С. Стивене. Мы сначала поднимаемся по лестнице, которая ни на чем не закреплена, и добираемся до лестницы, которая закрепле­на. Однако каким путем мы оказались на ней? Измерили некую психо­логическую переменную по шкале порядка, подсчитали средние и стан­дартные отклонения, а затем получили, наконец, интервальную шкалу. "Такому нелегальному использованию статистики может быть дано из­вестное прагматическое оправдание; во многих случаях оно приводит к плодотворным результатам" (Стивене С, 1960, с. 56).

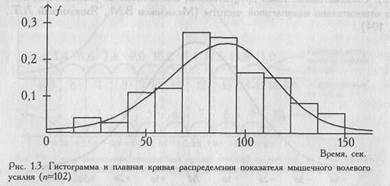
Многие исследователи не проверяют степень совпадения получен­ного ими эмпирического распределения с нормальным распределением, и тем более не переводят получаемые значения в единицы долей стан­дартного отклонения или процентили, предпочитая пользоваться "сырыми" данными. "Сырые" же данные часто дают скошенное, срезан­ное по краям или двухвершинное распределение. На Рис. 1.3 представле­но распределение показателя мышечного волевого усилия на выборке из 102 испытуемых. Распределение с удовлетворительной точностью мож­но считать нормальным (χ²=12,7, при v=9, M=89,75, σ= 25,1).

На Рис. 1.4 представлено распределение показателя самооценки по шкале методики Дж. Менестера - Р.Корзини "Уровень успеха, ко­торого я должен был достичь уже сейчас" (n=356). Распределение зна­чимо отличается от нормального (χ²=58,8, при v=7; p<0,01; М=80,64; σ =16,86).

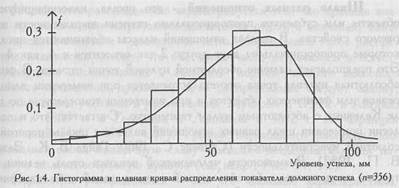
С такими "ненормальными" распределениями приходится встре­чаться очень часто, чаще, может быть, чем с классическими нормаль­ными. И дело здесь не в каком-то изъяне, а в самой специфике психо­логических признаков. По некоторым методикам от 10 до 20% испы­туемых получают оценку "ноль" - например, в их рассказах не встреча­ется ни одной словесной формулировки, которая отражала бы мотив "надежда на успех" или "боязнь неудачи" (методика Хекхаузена). То, что испытуемый получил оценку "ноль", нормально, но распределение таких оценок не может быть нормальным, как бы мы ни увеличивали объем выборки (см. п. 5.3).

Методы статистической обработки, предлагаемые в настоящем руководстве, в большинстве своем не требуют проверки совпадения по­лученного эмпирического распределения с нормальным. Они построены на подсчете частот и ранжировании. Проверка необходима только в случае применения дисперсионного анализа. Именно поэтому соответст­вующая глава сопровождается описанием процедуры подсчета необхо­димых критериев.

Во всех остальных случаях нет необходимости проверять степень совпадения полученного эмпирического распределения с нормальным, и тем более стремиться преобразовать порядковую шкалу в равноинтервальную. В каких бы единицах ни были измерены переменные - в се­кундах, миллиметрах, градусах, количестве выборов и т. п. - все эти данные могут быть обработаны с помощь непараметрических критери­ев[3], составляющих основу данного руководства.

Шкала равных отношений- это шкала, классифицирующая объекты или субъектов пропорционально степени выраженности изме­ряемого свойства. В шкалах отношений классы обозначаются числами, которые пропорциональны друг другу: 2 так относится к 4, как 4 к 8. Это предполагает наличие абсолютной нулевой точки отсчета. В физике абсолютная нулевая точка отсчета встречается при измерении длин от­резков или физических объектов и при измерении температуры по шка­ле Кельвина с абсолютным нулем температур. Считается, что в психо­логии примерами шкал равных отношений являются шкалы порогов аб­солютной чувствительности (Стивене С, 1960; Гайда В. К., Захаров В. П., 1982). Возможности человеческой психики столь велики, что трудно представить себе абсолютный нуль в какой-либо измеряемой психологической переменной. Абсолютная глупость и абсолютная чест­ность - понятия скорее житейской психологии.

То же относится и к установлению равных отношений: только метафора обыденной речи допускает, чтобы Иванов был в 2 раза (3, 100, 1000) умнее Петрова или наоборот.

Абсолютный нуль, правда, может иметь место при подсчете ко­личества объектов или субъектов. Например, при выборе одной из 3 альтернатив испытуемые не выбрали альтернативу А ни одного раза, альтернативу Б - 14 раз и альтернативу В - 28 раз. В этом случае мы можем утверждать, что альтернативу В выбирают в два раза чаще, чем альтернативу Б. Однако при этом измерено не психологическое свойст­во человека, а соотношение выборов у 42 человек.

По отношению к показателям частот возможно применять все арифметические операции: сложение, вычитание, деление и умножение. Единица измерения в этой шкале отношений - 1 наблюдение, 1 выбор, 1 реакция и т. п. Мы вернулись к тому, с чего начали: к универсальной шкале измерения в частотах встречаемости того или иного значения признака и к единице измерения, которая представляет собой 1 наблю­дение. Расклассифицировав испытуемых по ячейкам номинативной шка­лы, мы можем применить потом высшую шкалу измерения - шкалу от­ношений между частотами.

Распределение признака. Параметры распределения

Распределением признака называется закономерность встречаемо­сти разных его значений (Плохинский Н.А., 1970, с. 12).

В психологических исследованиях чаще всего ссылаются на нор­мальное распределение.

Нормальное распределение характеризуется тем, что крайние зна­чения признака в нем встречаются достаточно редко, а значения, близ­кие к средней величине - достаточно часто. Нормальным такое распре­деление называется потому, что оно очень часто встречалось в естест­веннонаучных исследованиях и казалось "нормой" всякого массового случайного проявления признаков. Это распределение следует закону, открытому тремя учеными в разное время: Муавром в 1733 г. в Англии, Гауссом в 1809 г. в Германии и Лапласом в 1812 г. во Франции (Плохинский Н.А., 1970, с.17). График нормального распределения представляет собой привычную глазу психолога-исследователя так на­зываемую колоколообразную кривую (см. напр., Рис. 1.1, 1.2).

Параметры распределения - это его числовые характеристики, указывающие, где "в среднем" располагаются значения признака, на­сколько эти значения изменчивы и наблюдается ли преимущественное появление определенных значений признака. Наиболее практически важными параметрами являются математическое ожидание, дисперсия, показатели асимметрии и эксцесса.

В реальных психологических исследованиях мы оперируем не па­раметрами, а их приближенными значениями, так называемыми оценка­ми параметров. Это объясняется ограниченностью обследованных выбо­рок. Чем больше выборка, тем ближе может быть оценка параметра к его истинному значению. В дальнейшем, говоря о параметрах, мы будем иметь в виду их оценки.

Среднее арифметическое (оценка математического ожидания) вы­числяется по формуле:

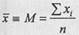
где x_i - каждое наблюдаемое значение признака;

i - индекс, указывающий на порядковый номер данного зна­чения признака;

п - количество наблюдений;

∑- знак суммирования.

Оценка дисперсии определяется по формуле:

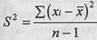
где x_i - каждое наблюдаемое значение признака;

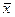- среднее арифметическое значение признака;

n - количество наблюдений.

Величина, представляющая собой квадратный корень из несме­щенной оценки дисперсии (S), называется стандартным отклонением или средним квадратическим отклонением. Для большинства исследова­телей привычно обозначать эту величину греческой буквой σ (сигма), а не S. На самом деле, σ - это стандартное отклонение в генеральной совокупности, a S - несмещенная оценка этого параметра в исследован­ной выборке. Но, поскольку S - лучшая оценка σ (Fisher R.A., 1938), эту оценку стали часто обозначать уже не как S, а как σ:

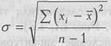
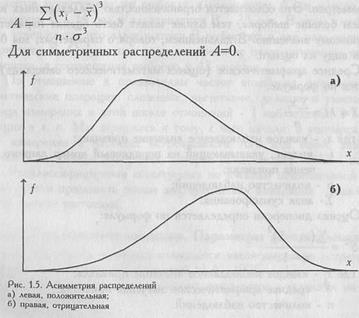
В тех случаях, когда какие-нибудь причины благоприятствуют более частому появлению значений, которые выше или, наоборот, ниже среднего, образуются асимметричные распределения. При левосторон­ней, или положительной, асимметрии в распределении чаще встречаются более низкие значения признака, а при правосторонней, или отрица­тельной - более высокие (см. Рис. 1.5).

Показатель асимметрии (A)вычисляется по формуле:

В тех случаях, когда какие-либо причины способствуют преиму­щественному появлению средних или близких к средним значений, об­разуется распределение с положительным эксцессом. Если же в рас­пределении преобладают крайние значения, причем одновременно и бо­лее низкие, и более высокие, то такое распределение характеризуется отрицательным эксцессом и в центре распределения может образоваться впадина, превращающая его в двувершинное (см. Рис. 1.6).

Показатель эксцесса (E) определяется по формуле:

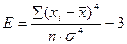
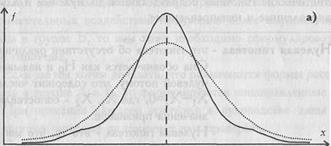
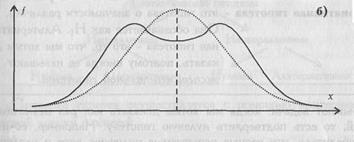
Рис. 1.6. Эксцесс: а) положительный; 6) отрицательный

В распределениях с нормальной выпуклостью E=0.

Параметры распределения оказывается возможным определить только по отношению к данным, представленным по крайней мере в интервальной шкале. Как мы убедились ранее, физические шкалы длин, времени, углов являются интервальными шкалами, и поэтому к ним применимы способы расчета оценок параметров, по крайней мере, с формальной точки зрения. Параметры распределения не учитывают истинной психологической неравномерности секунд, миллиметров и других физических единиц измерения.

На практике психолог-исследователь может рассчитывать пара­метры любого распределения, если единицы, которые он использовал при измерении, признаются разумными в научном сообществе.