Несимметричные режимы работы. Переходные процессы в трансформаторах

Несимметричный режим работы трансформаторов — это режим, когда токи в фазах первичной и вторичной обмот­ках трансформатора неодинаковы. Различают два вида не­симметричных режимов: либо вследствие несимметрии пер­вичных напряжений, либо вследствие несимметрии сопротив­лений вторичных или первичных цепей трансформаторов.

Несимметричный режим является наиболее общим случа­ем работы электрических машин и трансформаторов на прак­тике, поскольку в любой электрической системе имеется тот или иной вид несимметрии. В общем случае могут иметь мес­то одновременно оба вида несимметрии: несимметрия пер­вичных напряжений и несимметрия сопротивления цепи обмо­ток нагрузки трехфазного трансформатора. Симметричные режимы являются идеализированным случаем, удобным для теоретического анализа электрических машин и трансформа­торов, получаемым при известных допущениях.

Несимметричный режим возникает при подключении трех­фазного трансформатора к электрической системе с несим­метричной системой напряжений, а также при подключении к трехфазному трансформатору значительной однофазной на­грузки: электротермических печей, тяговых подстанций, освети­тельной нагрузки и др. При анализе несимметричных режимов трансформаторов учитывается схема соединения первичной и вторичной обмоток.

Предельными режимами несимметрии для трансформато­ров являются одно- или двухфазные короткие замыкания вто­ричной обмотки. К несимметричным режимам относятся также неполнофазные режимы, которые возникают при обрыве одного из фазных проводов.

Режимы короткого замыкания и неполнофазные режимы связаны с появлением недопустимо больших токов и являются аварийными, и трансформаторы, оказавшиеся в таких режимах, отключают от энергосистемы.

Как было показано выше, в симметричном режиме процес­сы в каждой фазе трансформатора происходят одинаково, поэтому их анализ для одной фазы дает полное представле­ние о процессах в трансформаторе в целом. В несимметрич­ных режимах различны не только фазные токи, но и магнит­ные потоки стержней, поэтому необходимо составлять и ре­шать одновременно уравнения для всех трех фаз. Поскольку в общем случае несимметричного режима сумма магнитных потоков фаз не равна нулю, картина распределения магнитно­го поля в сердечнике трансформатора разная в различных несимметричных режимах. Это делает неопределенной задачу определения взаимных индуктивностей фаз трансформатора в несимметричных режимах. Использование для решения этой задачи параметров и уравнений, характерных для симметрич­ного режима, приводит к недопустимым ошибкам.

Для анализа несимметричных режимов электрических ма­шин и трансформаторов, включая анализ режимов короткого замыкания, используют метод симметричных составляющих. В случае несимметрии первичного напряжения его разлагают на симметричные системы напряжений прямой и обратной последовательности. При несимметрии вторичных токов их разлагают на симметричные системы токов прямой, обратной и нулевой последовательности.

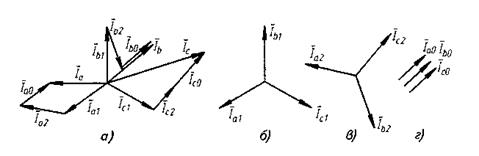
На рис. 2.25,a представлено разложение сугубо несиммет­ричной системы токов Ī_a, Ī_Ь и Ī_c на симметричные токи пря­мой (рис. 2.25,б), обратной (рис 2.25,в) и нулевой последова­тельности (рис. 2.25,г), которые отличаются друг от друга по­следовательностью прохождения токов через максимумы.

Рис. 2.25. Разложение несимметричной системы токов (а) на симметричные (б, в) и токи нулевой последовательности (г)

Токи, образующие систему прямой последовательности, достигают максимумов последовательно в фазах а, Ь, с. Токи, образующие систему обратной последовательности, достигают максимумов последовательно в фазах а, с, Ь. Токи же нулевой последовательности во всех трех фазах имеют одно направ­ление (нулевой сдвиг). В трансформаторе магнитные потоки разных последовательностей не влияют друг на друга, если не учитывать насыщение и гистерезис стали сердечника. Следо­вательно, для определения симметричной составляющей лю­бой переменной достаточно решить уравнения одной фазы трансформатора. Составляют уравнения:

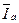⁼ Ī_а1+Ī_а2⁺Ī_а0,

Ī_b = Ī_b1+Ī_b2 +Ī₀, (2.50)

Ī_c = Ī_c1+Ī_c2+Ī_c0.

Вводится комплексный коэффициент а = е^j2π/3 .Умножение вектора на этот коэффициент не изменяет его абсолютного значения, но изменяет его аргумент на 2π/3, т. е. поворачивает вектор на угол 2π/3 = 120° в сторону вращения векторов. Умножение вектора на а² поворачивает вектор на угол 4π/3 — 240° в ту же сторону.

Полагают Ī_a0 = Ī_b0 = Ī_c0 = Ī_0П и, введя в уравнения (2.50) коэффициенты а и а¹, получают систему уравнений:

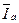⁼ Ī_а1⁺Ī_а2⁺Ī_0П,

Ī_b = a² Ī_а1⁺Ī_а2⁺Ī_0П , (2.51)

Ī_c = a Ī_а1⁺Ī_а2⁺Ī_0П.

После определения симметричных составляющих резуль­тирующие значения переменных находят их геометрическим сложением. Токи прямой, обратной и нулевой последователь­ностей можно выразить по системе уравнений (2.51) через несимметричные токи:

Ī_a1 = 1/3(Ī_a + aĪ_b + a²Ī_c),

I_a2 =1/3(Ī_a + a²Ī_b + aĪ_c), (2.52)

Ī_0П=1/3(Ī_a + Ī_b + Ī_c).

Достоинство метода состоит в том, что с симметричной системой каждой последовательности можно оперировать независимо от системы других последовательностей обычны­ми методами математического и графического анализа. Сле­дует, однако, учитывать, что метод симметричных составля­ющих основан на использовании принципа наложения, кото­рый справедлив только для линейных систем, поэтому прини­мается допущение, что сталь магнитопровода имеет линейные характеристики.

Далее, в отличие от вращающихся электрических машин в трансформаторе сопротивления прямой последовательности равны сопротивлениям обратной последовательности. Чтобы убедиться в этом, достаточно у трансформатора, работающего с симметричной нагрузкой, изменить порядок чередования фаз, т. е. поменять местами два провода из трех, с помощью кото­рых к первичной обмотке подводится напряжение сети. Тогда изменится на обратное чередование токов фаз трансформато­ра, однако, внутренние сопротивления трансформатора оста­ются неизменными. Поэтому токи обратной последовательно­сти трансформируются из вторичной обмотки в первичную так же, как и токи прямой последовательности и имеют те же схемы замещения, что и при анализе работы трансформатора в симметричных режимах. Это упрощает исследования работы трансформатора в несимметричных режимах, поскольку вмес­то отдельного рассмотрения составляющих прямой и обрат­ной последовательностей можно рассматривать их геометри­ческую сумму.

Сопротивления нулевой последовательности отличаются от сопротивлений прямой и обратной последовательностей по значению и по характеру, так как токи нулевой последо­вательности во всех трех фазах равны между собой, имеют одинаковое направление и их сумма не равна нулю. Сопротив­ления нулевой последовательности и схемы замещения для токов нулевой последовательности зависят как от схемы со­единения обмоток, так и от конструкции магнитной системы трансформатора.

При исследовании несимметричных режимов работы транс­форматора при всех соединениях его обмоток пренебрегают током холостого хода, и считают, что известны линейные пер­вичные напряжения, геометрическая сумма которых равна нулю, а также известны полные сопротивления нагрузки Z_a, Z_b, Z_c,

Рассмотрим в качестве примеров несимметричные режимы при соединении трансформаторов по схемам Y/Y₀.

С учетом этого обстоятельства, пренебрегая падениями напря­жений в первичной обмотке, уравнения для фазных напряже­ний первичной обмотки можно записать в виде:

Ū_A ^=-Ē_A-Ē₀,

Ū_B =-Ē_B-Ē₀, (2.53)

Ū_C = -Ē_C-Ē₀.

ЭДС Ē_A, Ē_B, Ē_C наведены симметричными системами по­токов прямой и обратной последовательности, в несимметрич­ном режиме они не равны, однако их геометрическая сумма равна нулю.

С учетом изложенного, на основании (2.53) можно по­строить векторную диаграмму первичных напряжений и ЭДС (рис. 2.26,б).

Искажение симметрии звезды первичных фазных ЭДС вы­зовет искажение симметрии вторичных фазных напряжений и ЭДС, поскольку их отношение всегда равно коэффициенту трансформации. Следовательно, на сопротивлениях нагрузки Z_a, Z_b, Z_c будут разные фазные напряжения. Во вторичной обмотке и в нулевом проводе проходит ток Ī₀ тем больший, чем больше величина несимметрии. Напряжение нулевой пос­ледовательности вторичной обмотки U₀ можно найти в ре­зультате разложения на симметричные составляющие систе­мы вторичных фазных напряжений.

Следует отметить, что несимметрия нагрузки возникает и в том случае, когда при прочих равных условиях различается характер сопротивлений нагрузки, например, преобладание в одной фазе активной нагрузки, в другой — индуктивной и т. д. Таким образом, токи нулевой последовательности, проходя по вторичным обмоткам, вызывают их дополнительный нагрев, тем больший, чем больше степень несимметрии. Поэтому при ожи­дании несимметричной нагрузки не следует соединять обмот­ки трансформатора по схеме Y/Y₀.

Схема ∆/Y₀ с нулевым проводомпредпочтительна при наличии ожидаемой значительной несимметрии нагрузки трансформатора. Покажем это. Во вторичной обмотке транс­форматора как и в предыдущем случае, вследствие несиммет­рии сопротивлений нагрузки возникает ток нулевой последова­тельности, создающий поток нулевой последовательности Ф_0Y. Этот поток индуцирует в фазах первичной обмотки одинаково направленные ЭДС

нулевой последовательности Ē_0∆. Их сумма равна 3 Ē_0∆. Под воздействием этой ЭДС в первичной обмотке, соединенной в ∆, будет циркулировать ток нулевой по­следовательности Ī_0∆, создающий поток Ф_0∆.

Суммарный поток от токов нулевой последовательности невелик, поскольку Ф_0∆ и Ф_0Y в значительной мере компенсиру­ют друг друга. Кроме того, результирующий поток нулевой последовательности по рассмотренным выше причинам будет замыкаться не по ярму магнитопровода, а по воздуху и по конструктивным стальным элементам трансформатора. Поэтому ЭДС нулевой последовательности, наводимые в обмотках малы, они практически не приводят при несимметричной нагрузке к искажению симметрии вторичных ЭДС.

По этой причине схема соединения обмоток трансформатора ∆/Y₀ рекомендуется ГОСТом как предпочтительное при ожидаемой существенной несимметрии нагрузки.