Замечательные точки треугольников

Теорема: Во всяком треугольнике перпендикуляры, восстановленные в серединах сторон пересекаются в одной точке.

Доказательство: Пусть дан треугольник DАВС. m^AB и проходит через середину АВ, l^AC и проходит через середину АС. Они пересекаются в точке О, так как не могут быть параллельны (почему?

)

Докажем, что прямая, проходящая через середину ВС перпендикулярно ей, проходит через точку О.

Т.к. точка О принадлежит прямой l, то она равноудалена от точек А и С, следовательно, ОА=ОС. Аналогично ОА=ОВ. Но тогда и ОС=ОВ, значит точка О равноудалена от точек В и С, т.е. лежит на серединном перпендикуляре к отрезку ВС.

Замечание: Точка пересечения серединных перпендикуляров – центр описанной окружности.

Теорема: Во всяком треугольнике все высоты пересекаются в одной точке

Доказательство: Пусть дан треугольник DАВС. Через вершину В проведем А'С'//АС. Через вершину А - В'С'//ВС. Через С - А'В'//АВ. Получим треугольник DА'В'С'. Докажем, что высоты треугольника DАВС являются серединными перпендикулярами DА'В'С'.

Пусть АD^ВС. По построению ВС// В'С', значит AD^ В'С'. Аналогично можно показать, что другие высоты перпендикулярны сторонам треугольника DА'В'С'. Покажем, что AD проходит через середину стороны В'С'. Действительно, т.к. четырехугольник С'ВСА – параллелограмм (почему?

),

то ВС=С'А, ВС'=АС. Изпараллелограмма АВСВ' аналогично получаем АВ=СВ' и ВС=АВ'.

Отсюда С'А=АВ', т.е. точка А – середина стороны С'В'. Значит, АD – серединный перпендикуляр к С'В'. Аналогично остальные высоты треугольника DАВС являются серединными перпендикулярами к сторонам треугольника DА'В'С', а значит, пересекаются в одной точке.

Замечание: Точка пересечения высот треугольника – ортоцентр треугольника.

Теорема: Биссектрисы внутренних углов треугольника пересекаются в одной точке

Доказательство: самостоятельно

Замечание: Точка пересечения биссектрис внутренних углов треугольника – центр вписанной окружности.

Теорема: Обобщенная теорема о биссектрисах углов треугольника

6 биссектрис внутренних и внешних углов треугольника пересекаются по три в четырех точках:

в одной из этих четырех точек пересекаются биссектрисы внутренних углов треугольника(1),

а в каждой из трех других – биссектрисы внешних углов при двух вершинах и биссектриса внутреннего угла при третьей вершине(2).

Доказательство: То, что биссектрисы внутренних углов треугольника пересекаются в одной точке, доказано в предыдущей теореме.

Рассмотрим второй случай.

Пусть n – биссектриса угла ÐDBC(ее точки равноудалены от сторон угла BD и BC)

l – биссектриса угла ÐBАC(ее точки равноудалены от сторон угла АB и АC)

m – биссектриса угла ÐЕCВ(ее точки равноудалены от сторон угла ЕС и CВ). Лучи n и m пересекутся в точке О, которая будет равноудалена от AD и АЕ ( почему?

)

т.е. точка О будет лежать на луче l, биссектрисе угла ÐВАС. Аналогично проводится доказательство для оставшихся двух случаев.

Теорема: Три медианы треугольника пересекаются в одной точке. Эта точка отсекает от любой медианы 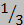часть, считая от соответствующей стороны.

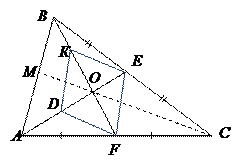Доказательство: Пусть ВК=КО и AD=DO. Тогда соединим отрезками точки DK и EF. В треугольнике DАВО DK – средняя линия. По свойству средней линии DK//AB и .

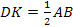EF – средняя линия треугольника DАВС, По свойству средней линии EF//AB и 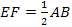. Отсюда DK= EF, т.е. DKEF – параллелограмм. Отсюда КО=ОF, DO=OE. Но КО=КВ, DO=AD. Значит, медианы разделены на три равные части и, в частности, 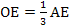, 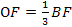. Аналогично рассматривается, что медианы АЕ и СМ пересекаются и отсекают точкой пересечения 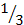, следовательно, СМ проходит через точку О.

Замечание: Точка пересечения медиан треугольника – центр тяжести треугольника.

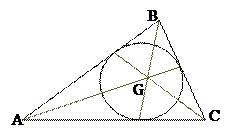
Прямые, соединяющие вершины треугольника с точками касания вписанной окружности проходят через одну точку, которая называется точкой Жергона