Треугольник и его элементы.

Треугольником называется множество трех точек, не лежащих на одной прямой, и трех отрезков, попарно соединяющих эти точки.

Элементами треугольника являются три стороны, три угла, три тройки отрезков: биссектрисы, медианы, высоты. Иногда к ним присоединяют еще серединные перпендикуляры к сторонам.

Высотой треугольника, опущенной из данной вершины, называется перпендикуляр, проведенный из этой вершины к прямой, содержащей противоположную сторону.

Биссектрисой треугольника называется отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны.

Медианой треугольника, проведенной из данной вершины, называется отрезок, соединяющий данную вершину с серединой противоположной стороны.

Средней линией треугольника называется отрезок, соединяющий середины двух его сторон.

Внешним углом треугольника при данной вершине называется угол, смежный с углом треугольника при этой вершине. Сами углы треугольника называют внутренними.

Теорема: Свойство средней линии треугольника

Средняя линия треугольника, соединяющая середины двух сторон треугольника, параллельна третьей стороне и равна ее половине

Доказательство: самостоятельно

Теорема: Сумма углов треугольника равна 180°

Доказательство: самостоятельно

Теорема: Внешний угол треугольника равен сумме двух внутренних углов треугольника, несмежных с ним

Доказательство: самостоятельно

Следствие: Внешний угол треугольника больше любого внутреннего угла треугольника, несмежного с ним.

Доказательство: самостоятельно

Треугольник называется равнобедренным, если у него две стороны равны.

Свойства равнобедренного треугольника:

1) В Равнобедренном треугольнике углы при основании равны

(обратно: Если в треугольнике два угла равны, то он равнобедренный)

2) Медиана, проведенная к основанию равнобедренного треугольника, является биссектрисой и высотой

(без доказательства)

Прямоугольным называется треугольник, у которого один угол прямой.

Теорема Пифагора

В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов

(без доказательства)

Два треугольника называются равными, если стороны и углы обоих треугольников соответственно равны

Основное свойство существования равных треугольников задается аксиомой:

· Каков бы ни был треугольник, существует равный ему треугольник в заданном расположении относительно данной полупрямой.

Предложения, известные как признаки равенства треугольников, дают необходимые и достаточные условия для того, чтобы два треугольника были равны.

(Сформулировать и доказать самостоятельно три признака равенства треугольников):

1)

2)

3)

4) Если два угла и сторона противолежащая одному из этих углов данного треугольника соответственно равны двум углам и стороне другого треугольника, то такие треугольники равны.

Доказательство:

ÐА=ÐА'

ÐВ=ÐВ'

ВС=В'С'

т.к. ÐА=ÐА'

ÐВ=ÐВ', то ÐС=ÐС'. Таким образом, по второму признаку равенства треугольников они равны.

5) Если две стороны и угол, лежащий против большей из этих сторон одного треугольника соответственно равен двум сторонам и углу другого треугольника, то такие треугольники равны.

Доказательство:

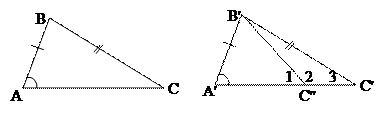АВ=А'В'

ВС=В'С'

ВС>АВ

В'С'>А'В'

ÐА=ÐА'

Методом от противного докажем, что АС=А'С'. Предположим, что АС≠А'С' и для определенности будем считать, что АС<А'С'. Тогда выберем на А'С' такую точку С'', что АС=А'С''. Тогда треугольник DА'В'С''=DАВС (почему?

)

. Отсюда ВС= В'С'', но по условию ВС= В'С', таким образом, треугольник В'С'С'' – равнобедренный, а по свойству равнобедренного треугольника углы Ð2=Ð3. Но Ð1>Ð3 (почему?

)

и Ð2>ÐA' ( почему? )

Таким образом, Ð1>Ð3, но Ð3=Ð2, а Ð2>ÐA', т.е. получаем, что Ð1>ÐA'. из чего следует, что

А'В'> В'С''(почему? ).

Но В'С''=ВС, следовательно, А'В'>ВС что невозможно по условию. Таким образом, АС= А'С' и треугольники DА'В'С'=DАВС равны по первому признаку.