Теорема умножения вероятностей независимых событий

Сформулируем теорему умножения вероятностей независимых событий.

Теорема. Вероятность совместного появления двух независимых событий А и В равна произведению вероятностей этих событий:

Для того чтобы обобщить теорему умножения на несколько событий, введем понятие независимости событий в совокупности.

Определение. Несколько событий называют независимыми в совокупности, если каждое из них и любая комбинация остальных событий (содержащих либо все остальные события, либо часть из них) есть события независимые.

Например, если события А₁, А₂ и А₃ независимые в совокупности, то независимыми являются события: А₁ и А₂, А₁ и А₃, А₂ и А₃, А₁А₂ и А₃, А₁А₃ и А₂, А₂А₃ и А₁.

Подчеркнем, что если несколько событий независимы попарно, то из этого еще не следует их независимость в совокупности. В этом смысле требование независимости событий в совокупности сильнее требования их попарной независимости.

Теперь мы можем сформулировать следствие из теоремы умножения вероятностей, обобщающее теорему умножения на несколько событий.

Следствие. Вероятность совместного появления нескольких событий, независимых в совокупности, равна произведению вероятностей этих событий.

Пример 2.4. Имеется три урны, содержащих по 10 шаров. В первой урне 5 шаров красного цвета, во второй – 4, в третьей – 6. Из каждой урны наудачу вынимают по одному шару. Найти вероятность того, что все три шара окажутся красного цвета.

Решение. Вероятность того, что из первой урны вынут шар красного цвета (событие А) Р(А) = 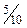= 0,5. Вероятность того, что из второй урны вынут шар красного цвета (событие В) Р(В) = 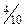= 0,4. Вероятность того, что из третьей урны вынут шар красного цвета (событие С) Р(С) = 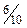= 0,6.

Так как события А, В и С независимые в совокупности, то искомая вероятность (по теореме умножения) равна

Р(АВС) = Р(А)·Р(В)·Р(С) = 0,5·0,4·0,6 = 0,12. ◄