Теорема сложения вероятностей несовместных событий
Теорема. Вероятность суммы несовместных событий равна сумме вероятностей этих событий:
| Р(А1 + А2 + … + Аn) = Р(А1) +Р(А2) + … + Р(Аn). | (2.1) |
Пример 2.2. В урне 10 шаров: 2 красных, 3 зеленых и 5 белых. Найти вероятность появления цветного шара.
Решение. Появление цветного шара означает появление либо красного (событие А), либо зеленого шара (событие В). Вероятность появления красного шара Р(А) = 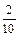 , вероятность появления зеленого шара Р(В) =
, вероятность появления зеленого шара Р(В) = 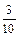 . События А и В несовместны, т.к. появление шара одного цвета исключает появление шара другого цвета. Следовательно, теорема сложения применима. Искомая вероятность
. События А и В несовместны, т.к. появление шара одного цвета исключает появление шара другого цвета. Следовательно, теорема сложения применима. Искомая вероятность
Р(А + В) = Р(А) +Р(В) = 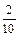 +
+ 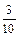 =
= 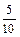 = 0,5. ◄
= 0,5. ◄
Отметим следствия, вытекающие из теоремы сложения вероятностей несовместных событий.
Следствие 1. Сумма вероятностей событий А1, А2, …Аn, образующих полную группу, равна единице.
| Р(А1) +Р(А2) + … + Р(Аn) = 1. | (2.2) |
Следствие 2. Сумма вероятностей противоположных событий равна единице:
Р(А) + Р( 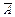 ) = 1. ) = 1.
| (2.3) |
Это следствие есть частный случай следствия 1. Оно выделено ввиду его большой важности для практического применения. При решении задач часто оказывается легче вычислить вероятность противоположного события 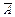 , чем прямого события А. В этом случае следствие 2 используется в виде
, чем прямого события А. В этом случае следствие 2 используется в виде
Р(А) = 1 – Р( 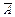 ). ).
| (2.4) |
Пример 2.3. Бросаются три игральных кости. Какова вероятность того, что сумма выпавших очков меньше 18?
Решение. В результате бросания трех игральных костей могут появиться 16 различных сумм очков от 3 до 18, которые образуют полную группу событий. Для решения задачи следует вычислить вероятность появления 15-ти сумм очков от 3 до 17, а затем сложить их. Это довольно трудоемкая операция. Поступим по-другому. Событие «сумма выпавших очков меньше 18» и событие «сумма выпавших очков равна 18» являются противоположными. Обозначим их А и 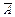 . Очевидно, что проще найти вероятность противоположного события.
. Очевидно, что проще найти вероятность противоположного события.
При бросании трех игральных костей общее число исходов n = 6·6·6 = 216. 18 очков могут выпасть только в одном случае, когда на всех костях выпадет по 6 очков, т.е. число благоприятных исходов m = 1. Таким образом, вероятность противоположного события Р( 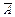 ) =
) = 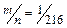 .
.
Зная вероятность противоположного события, находим вероятность интересующего нас события:
Р(А) = 1 – Р( 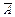 ) = 1 –
) = 1 – 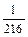 =
= 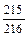 . ◄
. ◄
Прежде чем сформулировать теорему умножения вероятностей, введем понятие зависимых и независимых событий.
Дата добавления: 2021-12-14; просмотров: 490;











