ТЕМА 7. Семь новых инструментов контроля качества

План

Диаграмма сродства

Диаграмма зависимостей

Системная (древовидная) диаграмма

Матричная диаграмма

Стрелочная диаграмма

7.6 Диаграмма планирования оценки процесса

Анализ матричных данных

Схема потока

Диаграмма сродства

Эта диаграмма служит для определения причин нарушения процесса и их систематизации для облегчения поиска мер, направленных на их исключение. Например, важной задачей является нахождение правильных методов осуществления научных исследований и разработок с учетом условий, складывающихся в современном обществе в «эпоху высокоэффективных технологий». При этом важным оказывается вопрос, как изменить существующую систему обеспечения качества, чтобы она соответствовала новым требованиям. Каждая такая тема характеризуется множеством словесных данных. Диаграмма сродства представляет собой метод систематизации основных проблем, требующих решения, подобранных по принципу сродства того количества словесных данных, которое относится к этим проблемам.

Диаграмма зависимостей

Эта диаграмма составляется для того, чтобы проблемам, требующим разрешения, зафиксированным в диаграмме сродства, поставить в соответствие основные причины, вызвавшие их появление, например, диаграмма зависимостей, указывающая причины несовпадения параметров опытных образцов изделия по его проекту.

На диаграмме, показанной на рисунке 8.2 приведено 30 факторов, которые рассматриваются как первичные и вторичные причины несовпадения: зависимости между ними показаны стрелками. Классификация этих причин по важности осуществляется с учетом используемой технологии, числовых данных, характеризующих причины и т.д.

Чтобы оценить значимость взаимного влияния подсчитывают количество входящих и выходящих стрелок на каждом факторе.

Системная (древовидная) диаграмма

Диаграмма дерева исследует все возможные причины на основании множества последовательных шагов.

Эта диаграмма используется в качестве метода системного определения оптимальных средств решения возникших проблем и строится в виде многоступенчатой древовидной структуры, элементами которой являются различные средства и способы решения. Как правило, иерархические структуры типа «дерево». Применяется для анализа возможности решения некоторой сложной проблемы.

Анализ может осуществляться в разных аспектах, например, для:

- выявления тех подпроблем, совокупность которых отражает сущность сложной исходной проблемы (в этом случае дерево представляет собой дерево проблем);

- определения набора средств, с помощью которых может быть обеспечено решение исходной проблемы (дерево становится деревом средств или деревом мероприятий);

- обозначения или иерархического упорядочения тех целей, для достижения которых выполняется некоторый проект или программа (дерево целей);

- выбора оптимального набора средств, обеспечивающих решение исходной сложной проблемы (дерево решений);

- распространения ресурсов (например, финансовых), выделяемых для решения отдельных подпроблем сложной проблемы (дерево относительных важностей);

- прогнозирование возможности решения отдельных подпроблем сложной проблемы (дерево прогнозов).

Применяются и другие виды деревьев: дерево свойств, дерево показателей, дерево классификационное, дерево дефектов, дерево полезностей, дерево функций, дерево взаимосвязей, дерево ресурсов.

Практически все перечисленные выше виды деревьев могут рассматриваться как частные случаи дерева проблем. Поскольку оно наиболее часто используется на практике, последующий материал будет излагаться на наиболее часто встречающемся дереве проблем.

В современных условиях древовидные структуры наиболее часто и широко используются в системном анализе, прогнозировании, квалиметрии и в теории принятия решений.

Основное понятие – свойство (представлено одной из ветвей дерева).

Свойства бывают сложные (делимые на менее сложные) и простые (элементарные, неделимые).

В дереве проблем аналогом свойства является – проблема, в дереве целей – цель, в дереве ресурсов – ресурс и т.д.

Кроме сложных и простых в дереве свойств могут присутствовать так называемые квазипростые свойства. Это свойства, которые в силу того, что они являются сложными, могут быть разделены на группы менее сложных, однако нет необходимости подвергать их такому делению, поскольку известна функциональная или корреляционная зависимость между таким сложным свойством и группой менее сложных свойств.

В дереве свойств качество, как наиболее сложное свойство рассматривается в виде ствола дерева, который условно считают расположенным в 0-м ярусе дерева (рис. 6.1). Это сложное свойство делится на менее сложные свойства, каждое из которых, в свою очередь, делится на еще менее сложные и т.д. Причем свойства более низкого (К-1)-го яруса являются обобщающимися для соответствующих свойств последующего К-го яруса (К=1,2,…m, где m – номер самого высокого (последнего) яруса дерева свойств).

Рис. 6.1. Схема разделения свойств на более простые

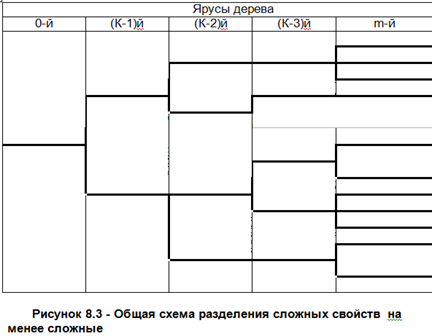
Кроме приведенных выше, в дереве свойств применяются и другие термины. Например:

- группа свойств – совокупность менее сложных свойств, на которую непосредственно раскладывается сложное свойство;

- высота дерева - общее число ярусов в дереве;

- полное дерево – такое дерево, на самом высоком ярусе которого расположены только простые или сверхпростые свойства;

- неполное дерево – дерево, разветвленное не до самого высокого яруса (т.е., имеющее на нем хотя бы одно сложное свойство);

- усеченное дерево – это полное или неполное дерево, из которого, в соответствии со спецификой конкретной, решаемой с помощью дерева задачи можно исключить одно или несколько свойств.

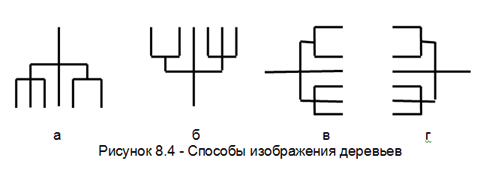
При построении (синтезе) деревьев в системном анализе, исследовании операций, чаще всего используют так называемое нижестороннее дерево (т.е. дерево, растущее вниз (рис. 6.2 а)). Реже верхнестороннее дерево (рис. 6.2 б) или правостороннее (растущее слева направо рис. 6.2 в). Совсем редко применяют левосторонее (т.е. растущее влево рис. 6.2 г).

Рис. 6.2. Способы построения деревьев

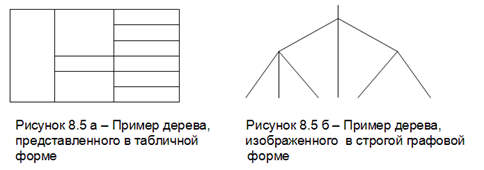
На практике применяются три основные формы изображения дерева: табличная форма (рис. 6.3 а), дающая возможность компактно (но не совсем наглядно) изобразить взаимосвязи элементов дерева и две так называемые графовые формы, менее компактные по сравнению с табличной, но обеспечивающие лучшую наглядность. Эти разновидности графовых форм: строгая графовая форма рис. 6.3 б).

Строгая графовая форма используется чаще всего в прогнозировании и исследовании операций.

Правила, регламентирующие выбор типа дерева:

- полное дерево при применении точного метода решения задачи (решение задачи количественного сравнения двух объектов по их качеству с минимальной погрешностью);

- усеченное дерево при применении шкалы рангов (если количественные результаты сравнения объектов по качеству допустимо выразить в шкале рангов).

- неполное дерево при применении упрощенного метода решения задачи.

Рис. 6.3. Примеры построения деревьев

Каждое свойство, входящее в группу свойств должно быть необходимым для адекватного описания связанного с этой группой сложного свойства, расположенного на дереве свойств на один ярус ниже, и, одновременно, количество этих свойств должно быть достаточным для обеспечения выше адекватного описания.

Число свойств в группе должно быть минимальным, не более семи-девяти.

Правильное построение дерева – важное условие, в решающей степени влияющее на достоверность получаемой при оценивании качества объекта информации.

Предположим, что фактор «много бракованных деталей, получаемых по внешнему заказу» на диаграмме зависимостей является наиболее важным фактором. В этом случае проблемой, требующей решения, будет «Снижение брака деталей, получаемых по внешнему заказу». Меры, применяемые для решения возникшей проблемы, выбираются с учетом самых разных факторов, таких как руководство фирмой, на которой размещен заказ, уровень техники на фирме-заказчике, уровень техники контроля и т.д.

В правой части диаграммы обычно приводится оценка мер по их важности и подробное пояснение способа выполнения намеченной меры.