Определение аналогов ускорений в механизме

Рассмотрим построение плана аналогов ускорений для кривошипно-ползунного механизма, (рис. 30)

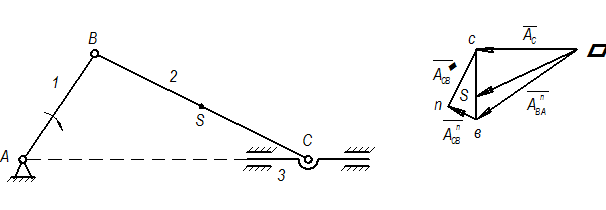
Рис. 2.30

Определяем сначала аналоги угловых скорости звеньев. Они могут быть определены с помощью МЦВ звена, либо с помощью построения полярного плана аналогов скоростей.

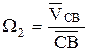
Затем строим план аналогов ускорений в такой последовательности:

От произвольно выбранного полюса откладываем вектор центростремительного ускорения точки В 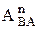в размере кривошипа АВ в направлении от В к А.

Для определения вектора аналога абсолютного ускорения точки С решаем совместно 2 векторных уравнений

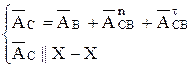
(2.5)

Здесь вектор аналога центростремительного относительного ускорения 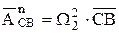и направление его совпадает с направлением СВ от С к В (центру вращения звена). Конец вектора обозначаем "n". Из n проводим вектор аналога тангенциального ускорения до пересечения с направлением вектора аналога абсолютного ускорения 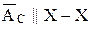. Точка пересечения этих двух направлений и даст нам конец вектора аналога абсолютного ускорения точки С ( ).

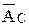Величина аналога ускорения определится так

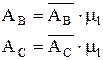
Величина ускорения определится так

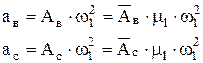
Вектор аналога ускорений точки 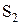определится построением точки 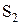на плане аналогов ускорений.

Аналоги угловых ускорений звеньев определятся из равенств

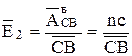
Угловое ускорение звена определится как

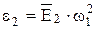
Рассмотрим построение плана ускорений для кулисного механизма, (рис. 2.31).

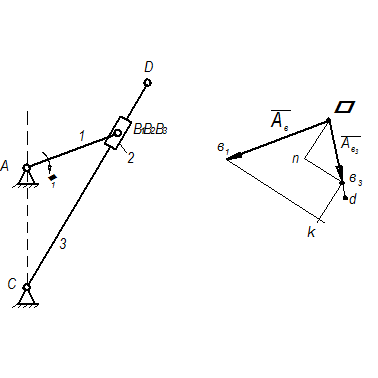
Рис. 2.31

Порядок построения плана:

Из полюса 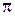откладываем вектор аналога центростремительного ускорения точку 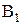, направление которого совпадает с направлением кривошипа, а длина равна радиусу кривошипа

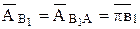
Аналог ускорение точки 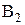ползуна равен ускорению точки 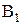, т.к. они соединены вращательной парой.

Ускорение точки 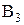, принадлежащей кулисе, находим, решив совместно два векторных уравнения

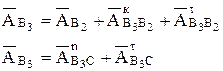
где, 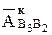- изображение на чертеже аналога кориолисова ускорения.

Аналог кориолисова ускорения находится по формуле

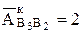
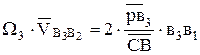
Вектор кориолисова ускорения всегда перпендикулярен кулисе и направлен в ту же сторону, что и аналог повернутой относительной скорости 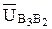, если 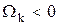. Если 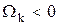(то есть вектор 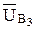направлен от центра вращения), то кориолисово ускорение направлено в сторону противоположную .

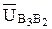Если пользоваться полярным планом аналогов скоростей, то для нахождения направления 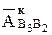нужно аналог относительной скорости 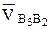повернуть на 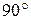в сторону вращения кулисы.

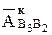- изображение аналога релятивного ускорения, направленного по кулисе.

Из конца вектора 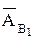проводим вектор 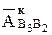. Из конца последнего проводим прямую линию, параллельную кулисе. Эта прямая определяет геометрическое место релятивного ускорения .

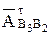В соответствии со вторым векторным уравнением из полюса 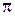откладываем вектор аналога центростремительного ускорения точки 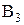относительно С, причем

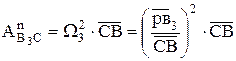
и совпадает с кулисой, то есть 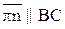. Затем из конца вектора 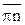проводим прямую линию перпендикулярно кулисе, эта прямая является направлением аналога вращательного ускорения .

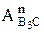Точку пересечения последней линии с направлением релятивного ускорения обозначим " 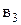". Таким образом, отрезки

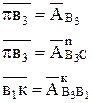
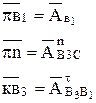
Аналоги ускорения найдутся следующим образом

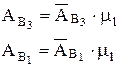и т.д.

Величина ускорений найдется так

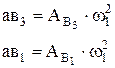и т.д.

Аналог углового ускорения кулисы

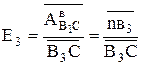
величина углового ускорения равна