Кинематическое исследование рычажных механизмов аналитическим методом
Аналитическое исследование дает возможность получить зависимости кинематических параметров механизма и, следовательно, достичь более точных результатов, чем при графическом методе. В настоящее время этот метод получает все большее распространение благодаря внедрению в практику ЭВМ.
Аналогии скоростей и ускорений, при кинематическом исследовании механизмов, скорости и ускорения ведомых звеньев и точек, удобно выражать в функции поворота 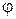 или перемещения S ведущего звена.
или перемещения S ведущего звена.
Функцией положения ведомого звена называется зависимость его перемещения от перемещения ведущего звена. Вид функции положения зависит от схемы механизма, а значения постоянных, которые входят в нее - от размерных параметров механизма. Для того чтобы составить функцию положения механизма, следует рассмотреть фигуру, которую образуют оси его звеньев. Из геометрических свойств этой фигуры находят искомую зависимость.
Аналогом скорости точки называется первая производная радиуса - вектора точки по обобщенной координате.
Аналогом ускорением точки называется вторая производная радиуса - вектора точки по обобщенной координате механизма.
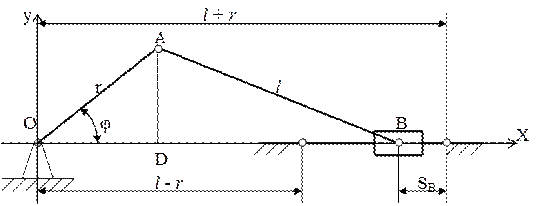
Кинематическое исследование проведем на примере кривошипно-ползунного механизма (рис 2.33).
Пусть заданы размеры центрального кривошипно-ползунного механизма
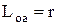 ;
; 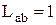 ;
;
и угловая скорость 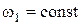 .
.
Независимым параметром является угол поворота
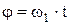 .
.
|
| Рис. 2.33 |
Выведем формулы для определения скорости 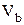 , и ускорения
, и ускорения 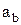 ползуна.
ползуна.
За время поворота кривошипа на угол 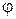 перемещение т. B будет:
перемещение т. B будет:
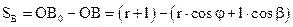
или
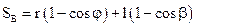
| (2.8) |
по теореме синусов можно написать: 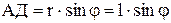
откуда
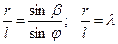 - коэффициент шатуна
- коэффициент шатуна
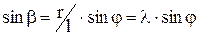 , a
, a
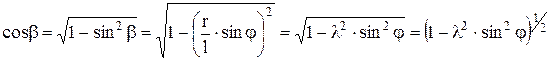
Разложим двучлен в ряд по формуле Бинома Ньютона
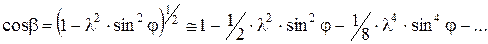
тогда
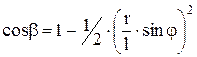
Пренебрегаем всеми членами, начиная с третьего в виду их малости. Подставляем значение 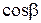 в формулу для перемещения S, получим:
в формулу для перемещения S, получим:
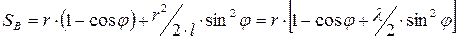
Последовательно дифференцируя получим скорость т.В
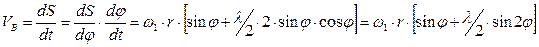
Ускорение т. В
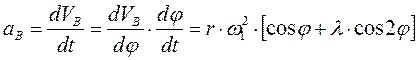
Формулы для шатуна
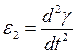
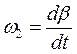
Дата добавления: 2021-12-14; просмотров: 543;











