Основное уравнение динамики вращающегося тела
Пусть твердое тело под действием внешних сил  (эти силы на рисунке не показаны) вращается около оси OZ с угловым ускорением
(эти силы на рисунке не показаны) вращается около оси OZ с угловым ускорением  . Алгебраическая сумма моментов всех сил (активных сил и сил сопротивления) относительно оси OZ ,
. Алгебраическая сумма моментов всех сил (активных сил и сил сопротивления) относительно оси OZ ,
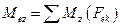
называется вращающим моментом.
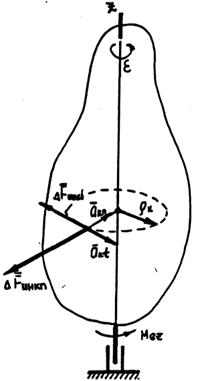
Рассматривая твердое тело как механическую систему, разобьем его на множество материальных точек с массами 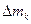 . Каждая из этих точек движется по окружности радиуса
. Каждая из этих точек движется по окружности радиуса 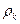 , с ускорением
, с ускорением  , которое разложим на касательное
, которое разложим на касательное 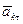 . и нормальное
. и нормальное  ускорения.
ускорения.
Приложим к каждой материальной точке элементарные силы инерции: касательную 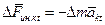 и нормальную
и нормальную  . Согласно принципу Даламбера, активные силы, силы реакции связей и силы инерции образуют уравновешенную систему. Поэтому алгебраическая сумма моментов всех этих сил относительно оси OZ должна быть равна нулю, т.е.
. Согласно принципу Даламбера, активные силы, силы реакции связей и силы инерции образуют уравновешенную систему. Поэтому алгебраическая сумма моментов всех этих сил относительно оси OZ должна быть равна нулю, т.е.

(моменты сил 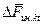 относительно оси OZ равны нулю, т. к. линии действия этих сил пересекают ось).
относительно оси OZ равны нулю, т. к. линии действия этих сил пересекают ось).
У любой точки вращающегося тела числовое значение касательного ускорения 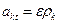 , поэтому значение
, поэтому значение 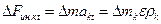 , где
, где 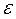 – угловое ускорение тела.
– угловое ускорение тела.
 .
.
Величина  равная сумме произведений масс всех точек тела на квадраты их расстояний от оси вращения, называется моментом инерции тела (системы) относительно этой оси.
равная сумме произведений масс всех точек тела на квадраты их расстояний от оси вращения, называется моментом инерции тела (системы) относительно этой оси.
Основное уравнение динамики вращающегося тела:
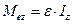
В СИ момент инерции тела выражается в 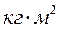 .
.
Дата добавления: 2021-12-14; просмотров: 403;











