Уравнение центральной винтовой оси

Пусть в центре приведения, принятом за начало координат, получены главный вектор 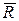с проекциями на оси координат R_х, R_у, R_z и главный момент 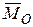с проекциями М_х, М_у, М_z. При приведении системы сил к центру приведения О₁ (рис.9.9) пусть получается динама с главным вектором 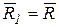и главным моментом 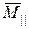. Векторы, образующие динаму, параллельны и поэтому могут отличаться только скалярным множителем p – шагом динамы . Имеем

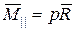. (9.6)

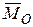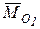Главные моменты и , согласно (9.2), удовлетворяют соотношению

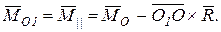
Подставляя 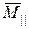из (9.2) в (9.6), получим

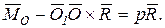(9.6 ^' )

Координаты точки О, в которой получена динама, обозначим через х, у, z. Тогда проекции вектора 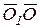на оси координат равны координатам х, у, z. Учитывая это, (9.6 ^' ) можно выразить в форме

,

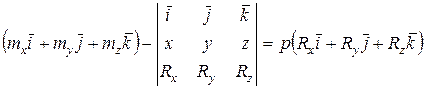где 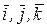- единичные векторы осей координат, а векторное произведение представлено определителем. Проецируя векторное уравнение (9.6 ^' ) на оси X, Y, Z, получим три скалярных уравнения, которые можно представить в виде

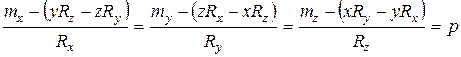. ( 9.7)

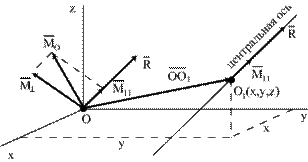
	Линейные уравнения (9.7) для координат х, у, z являются уравнениями прямой линии – центральной винтовой оси.
Рис.9.9

Пример. К твердому телу приложена система сил: F₁=1 Н, направленная по Оz, и F₂=1 Н, направленная параллельно ОY, как указано на рис.9.10а, где ОА=1м. Привести систему сил к простейшему виду.

Решение. Вычислим главный вектор 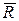и главный момент 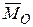. Проекций этих векторов на оси координат имеют вид

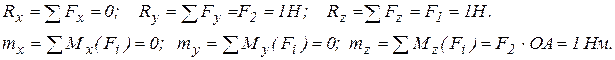Модули главного вектора и главного момента имеют значения (рис.9.10б):

а		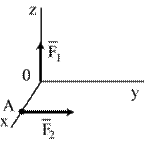б		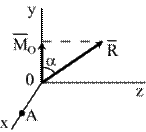в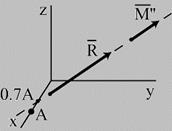
Рис.9.10

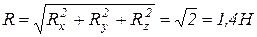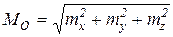; =1Н м.

Определим угол между векторам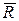и и 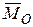и значение :

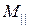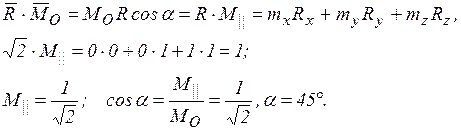
Так как 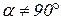, то силы приводятся к динаме.

Определим координаты центральной винтовой оси. Согласно (9.7), имеем

,

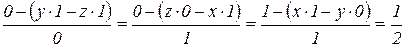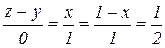или

, или .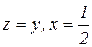

Центральная ось проходит через середину отрезка АО, ортогональна оси ОX и составляет углы 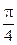с осями ОY и ОZ (рис.9.10в).