Изменение главного момента при перемене центра приведения
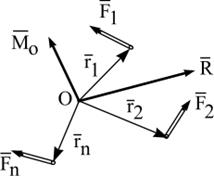
Согласно теореме Пуансо, произвольная система сил приводится к главному вектору 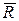 и главному моменту
и главному моменту 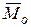 (
( 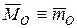 ) относительно произвольного центра приведения
) относительно произвольного центра приведения 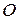 (рис. 9.1):
(рис. 9.1):
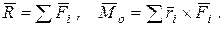 (9.1)
(9.1)
| Здесь 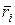 - радиус - вектор точки приложения силы - радиус - вектор точки приложения силы 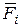 , проведенный из центра О.
При перемене центра приведения векторные моменты сил изменяются, так как изменяются радиус-векторы точек приложения (рис. 9.2). , проведенный из центра О.
При перемене центра приведения векторные моменты сил изменяются, так как изменяются радиус-векторы точек приложения (рис. 9.2).
|
| Рис. 9.1 | |
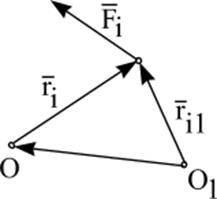
| Вследствие этого изменяется главный момент. Оценим изменение главного момента заданной системы сил. Из рис. 9.2 видно, что
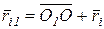 ,
где ,
где 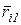 - радиус - вектор точки приложения силы - радиус - вектор точки приложения силы 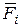 , проведенный из центра , проведенный из центра 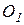 . .
|
| Рис. 9.2 |
Тогда главный момент системы 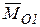 относительно нового центра приведения запишется
относительно нового центра приведения запишется
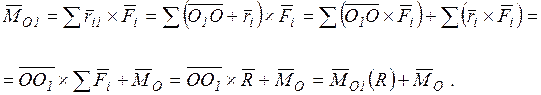
Здесь 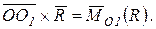
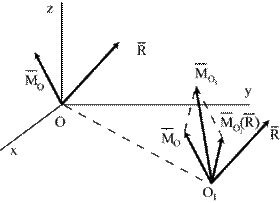
Получили, что главный момент относительно нового центра приведения (точка О1) (рис. 9.3) является векторной суммой моментов 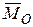 и и 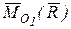 , т.е. , т.е.
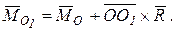 (9.2) (9.2)
| 
|
| Рис.9.3 |
Итак, главный момент системы сил при перемене центра приведения изменяется на векторный момент главного вектора 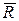 , приложенного в старом центре приведения относительно нового центра приведения О1.
, приложенного в старом центре приведения относительно нового центра приведения О1.
9.2. Инварианты системы сил
Физические величины инвариантны относительно данного преобразования координат, если значения этих величин не меняются при переходе к другой системе координат.
Главный вектор для любого центра приведения выражается векторной суммой: 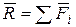 . Таким образом, главный вектор системы сил является векторным инвариантом. Для одной и той же системы сил он не зависит от выбора центра приведения.
. Таким образом, главный вектор системы сил является векторным инвариантом. Для одной и той же системы сил он не зависит от выбора центра приведения.
Получим второй скалярный инвариант. Для этого умножим правую и левую части уравнения (9.2) скалярно на 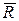 , получим
, получим
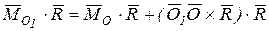 , (9.3)
, (9.3)
или
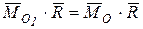 , (9.4)
, (9.4)
так как смешанное произведение векторов, содержащих два одинаковых множителя R, равно нулю, т.е. 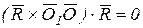 .
.
Как видно из соотношения (9.4), скалярное произведение главного момента на главный вектор не зависит от центра приведения, т.е. является вторым скалярным инвариантом: Выражение (9.4) можно записать так:
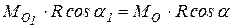 ,
,
где 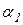 - угол между векторами
- угол между векторами 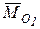 и
и 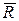 , а
, а 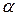 - между
- между 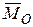 и
и 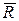 (рис. 9.4). После сокращения на R получим
(рис. 9.4). После сокращения на R получим
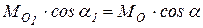 . (9.5)
. (9.5)
| Проекция главного момента на направление главного вектора не зависит от центра приведения. Разложим главный момент в каждом центре приведения на две взаимно перпендикулярные | 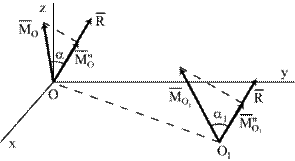
|
| Рис.9.4 |
составляющие, одна из которых направлена по главному вектору 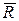 . Учитывая, что главные векторы в различных центрах приведения согласно (9.5) равны, получим (рис.9.4):
. Учитывая, что главные векторы в различных центрах приведения согласно (9.5) равны, получим (рис.9.4):
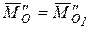 .
.
Дата добавления: 2019-12-09; просмотров: 1194;











