Замещаемость производственных факторов

Увеличение использования одного фактора при определенном объеме выпуска продукта всегда будет сопровождаться уменьше­нием количества другого фактора. Так, например, движение из точки C₁ в С₂, лежащих на одной изокванте не приводит к изме­нению объема производства, то есть ∆Q = 0 (рис. 21). Но при этом сокращаются затраты капитала на ∆К и увеличиваются зат­раты труда на ∆L. Отношение (-∆K/∆L) показывает замещение одного фактора производства другим при сохранении постоянно­го объема продукции и называется предельной нормой техноло­гического замещенияMRTS.

Нередко используют положительную величину отношения (-∆K/∆L). Если факторы производства бесконечно делимы, то

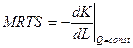
В рассматриваемом случае переменные факторы — аргумен­ты производственной функции Q = f(L, К) получают прираще­ния ∆L и ∆К, а функция — приращение ∆Q:

∆Q = f(L + ∆L, К + ∆К) - f(L,K).

Функция Q получает частное приращение, если ∆L ≠ 0, а ∆К = 0, то есть К остается неизменным; или если ∆L = 0, то есть L неизменно, а ∆KL ≠ 0. Частное приращение ∆_LQ при ∆L ≠0 равно:

∆_LQ = f(L + ∆L,K) - f(L,K) ≈ f`_L∆L ≈ f_LdL,

∆_KQ = f(L,K +∆K)- f(L,K) ≈ f`<sub>K</sub> ∆K ≈ f`_KdK.

Отсюда

dQ_L = f'_LdL,dQ_K = f`_KdK ,dQ = dQ_L + dQ_K.

Полный дифференциал производственной функции dQ равен сумме частных дифференциалов:

dQ = f`<sub>L</sub>dL + f`_KdK = 0, f`<sub>L</sub>dL = -f`_KdK.

В итоге получаем:

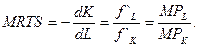
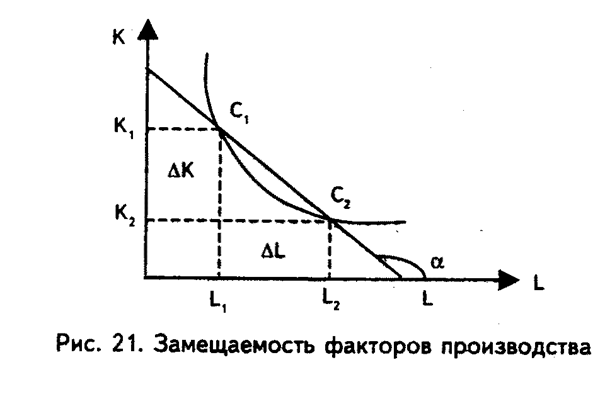
Отношение -∆K/∆L = tg(π - α) = -tg α есть угловой коэффици­ент касательной к изокванте в точке С₂, а абсолютное значение углового коэффициента изокванты представляет предельную нор­му технологического замещения труда капиталом.

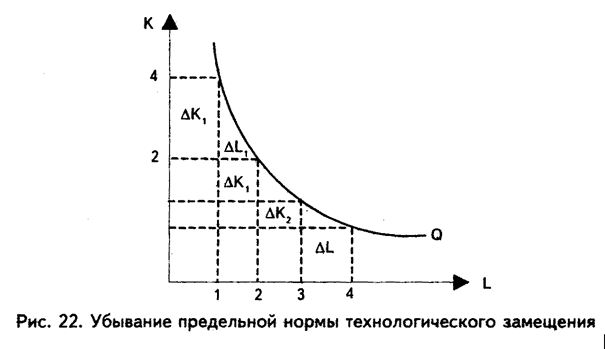
MRTS уменьшается по мере движения вниз вдоль изокванты. Это означает, что кривая имеет вогнутую относительно начала координат форму и что действует закон убывающей предельной нормы технологического замещения ресурсов (рис. 22).

Когда затраты труда увеличиваются с 1 до 2 (рис. 22), то про­исходит замещение капитала трудом и затраты капитала уменьша­ются при неизменном выпуске продукции вдоль изокванты. Труд становится менее производительным, а использование капитала все более эффективным. И наоборот, когда труд замещается боль­шим количеством капитала, отдача капитала снижается. Так, в США и Канаде на сельскохозяйственных фермах с высоким со­отношением капитала к труду MRTS относительно низка, в раз­вивающихся странах с низким соотношением капитала к труду MRTS высока.

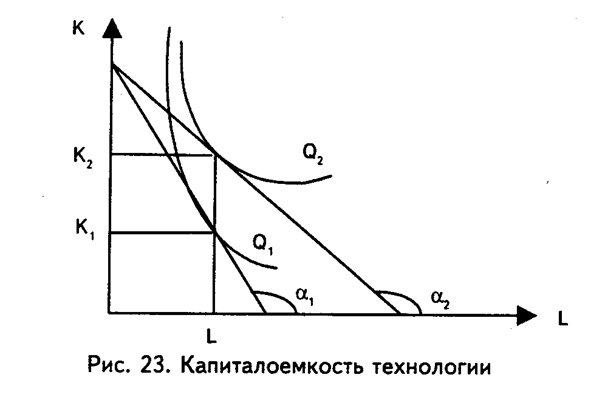
Капиталоемкость технологии определяется коэффициентом капитал/труд K/L, от которого зависит выпуск Q. На рис. 23 представлены изокванты двух фирм с выпуском Q₁ и Q₂, с одни­ми и теми же затратами труда L и различными затратами капи­тала К₁ > К₂.

Более высокой капиталоемкости K₂/L > K₁/L соответствует больший объем производства Q₂> Q₁. Наклон изокванты Q₁ превы­шает наклон Q₂, то есть tgα₁ > tgα₂, а угол α₂ наклона изокванты Q₂ с положительно направленной осью OL больше такого же угла α₁ изокванты Q₁. Это значит, что предельная норма замены труда капиталом в технологии Q₁ превышает предельную норму замены в технологии Q₂ и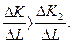

Но так как 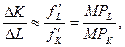то 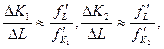и следовательно,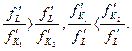

На единицу предельного продукта труда MP_L = f`_L предельный продукт капитала 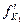при технологии Q₁ меньше, чем продель­ный продукт 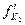при технологии Q₂. Если к обоим производствен­ным процессам добавляется единица труда, то из процесса Q₂, следует изъять меньшее количество капитала, чем из процесса Q_x, что подтверждает более высокую капиталоемкость процесса Q₂ по сравнению с капиталоемкостью процесса Q₁.

Эластичность замены труда капиталомразработана Д.Р. Хиксом. Производитель находится на одной и той же изокванте. Эластичность замены σравна относительному (процентному) изменению соотношения между двумя факторами, деленному на отно­сительное изменение предельной нормы технологического заме­щения. Эластичность замены капитала трудом σ_L и труда капи­талом σ_к равны:

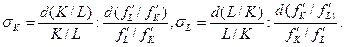
Запишем полные дифференциалы через частные производные и дифференциалы аргументов.

Таким образом, можно говорить об эластичности замены между трудом и капиталом и определять ее по формуле:

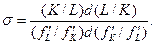
Каков экономический смысл эластичности замены? Предпри­ниматели стремятся использовать факторы производства в соче­тании, которое позволяет получить наибольший общий выпуск продукции в денежном выражении. Если замена одного фактора производства другим позволяет достичь такого результата, то ее обязательно осуществляют. Учитывая выражение MRTS в фор­муле, эластичность замены в том виде, как она представлена, устанавливает зависимость между темпом роста относительных затрат факторов 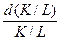и темпом роста предельной нормы заменымежду трудом и капиталом 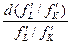или темпом роста коэффициента относительных цен факторов. Эластичность заме­ны можно рассматривать как меру пределов осуществимости за­мены капитала трудом или труда капиталом, как меру техноло­гической «однородности» факторов производства, которая ока­зывает влияние на выпуск продукции.

Эластичность может принимать любые значения от нуля до бесконечности. Повышение эластичности всегда ускоряет, а по­нижение ее сокращает темп роста выпуска. Эластичность связа­на с конфигурацией изоквант, чем больше кривизна изоквант, тем меньше эластичность замены.